Sommaire
Introduction
Principe général
Calcul de xmax et réactif limitant
Proportions stœchiométriques
Exercices
Dans ce chapitre nous allons voir comment remplir un tableau d’avancement et ce qu’il signifie.
Ce chapitre est très important car dans presque tous les sujets de chimie (en contrôle ou au bac) tu auras au moins un tableau d’avancement à réaliser !
Pour bien comprendre ce chapitre il faut bien maîtriser les réactions chimiques (coefficients stœchiométriques, savoir équilibrer une réaction etc…) ce pourquoi tu es invité (si ce n’est pas déjà fait) à bien apprendre le chapitre sur les réactions chimiques.
On va prendre une équation un peu générale (simple pour commencer) : imaginons que l’on ait deux réactifs A et B, qui réagissent pour donner deux produits C et D.
On va supposer dans un premier temps que les coefficients stœchiométriques sont 1 pour chaque espèce, on a donc la réaction suivante :
A + B → C + D.
On a forcément une certaine quantité de matière de A et de B (puisque ce sont les réactifs) que l’on va noter n0 et n1 : ce sont les quantités de matières initiales (à t = 0 s) des réactifs.
On rappelle que n0 et n1 sont en mol.
En revanche il n’y a ni de C ni de D à l’instant initial puisque ce sont les produits (ils apparaîtront au fur et à mesure de la réaction).
On va introduire une variable x, appelée avancement (en mol), qui va décrire l’évolution de la réaction.
A l’instant initial, x = 0 mol puisque la réaction n’a pas encore commencé.
Au fur et à mesure que la réaction va se dérouler, x va augmenter jusqu’à atteindre une valeur maximale, notée xmax.
—
A retenir : l’avancement x est en mol.
x = 0 mol à l’instant initial
x va augmenter au cours de la réaction jusqu’à atteindre une valeur maximale, notée xmax
x est donc toujours positif !
—
On va récapituler tout cela dans un tableau appelé tableau d’avancement.
Nous allons construire les différentes lignes au fur et à mesure.
La première ligne correspond à l’équation, mais il faut rajouter deux colonnes à gauche : une pour décrire l’état du système, l’autre pour donner la valeur de l’avancement :
| Etat du système | Avancement | A | + | B | → | C | + | D |
On va ensuite rajouter une ligne correspond à l’état initial du système.
—
Remarque : les valeurs du tableau d’avancement correspondent aux quantités de matière des espèces et sont donc toujours en mol, il n’y a donc pas besoin de la préciser !
—
| Etat du système | Avancement | A | + | B | → | C | + | D |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 |
En effet, on a vu qu’à l’instant initial, il y avait n0 mol de A, n1 mol de B et 0 mol de C et de D.
Ensuite, avant de passer à l’état final, on va rajouter une ligne pour décrire l’état intermédiaire du mélange réactionnel.
On se place donc à un instant t quelconque, et l’avancement est noté x, comme une variable !
Pour les quantités de matière : celle des réactifs diminue, celle des produits augmente. Oui, mais de combien ??
Celle des réactifs diminue de x, celle des produits augmente de x, tout simplement !
—
Remarque : nous verrons par la suite que c’est un peu plus complexe que cela mais pour l’instant retiens ce principe.
—
La quantité de matière de A est donc n0 – x, celle de B n1 – x, celle de C et D 0 + x, donc x.
On peut donc rajouter la ligne suivante :
| Etat du système | Avancement | A | + | B | → | C | + | D |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 | |||
| Etat intermédiaire | x | n0 – x | n1 – x | x | x |
Il reste maintenant à rajouter une ligne pour l’état final du système.
Comme on l’a dit l’avancement vaut alors xmax. Il suffit alors de remplacer tous les x de la ligne « état intermédiaire » par xmax (oui c’est très simple !  ) :
) :
| Etat du système | Avancement | A | + | B | → | C | + | D |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 | |||
| Etat intermédiaire | x | n0 – x | n1 – x | x | x | |||
| Etat final | xmax | n0 – xmax | n1 – xmax | xmax | xmax |
Et voilà c’est fini !
Enfin presque… on peut bien sûr remplacer n0 et n1 par les valeurs données dans l’énoncé ou que l’on aura calculé auparavant.
—
Remarque : la colonne « Etat du système » est un peu redondante avec la colonne « Avancement », donc avec le temps tu pourras mettre seulement une des deux, mais rien ne t’empêches de mettre les deux !
De même, la ligne « Etat intermédiaire » n’a parfois pas d’utilité donc tu pourras t’en passer, mais dans ce cours nous mettrons tout systématiquement pour t’habituer !
Bien sûr il faudra t’adapter à ce que te dis ton professeur en classe 
—
En réalité, c’est un tout petit peu plus complexe que cela comme dit précédemment.
En effet, les coefficients stœchiométriques ne sont pas toujours égaux à 1 comme dans l’exemple.
Imaginons que l’on ait plutôt l’équation :
A + 3B → 4C + D.
Le tableau va être exactement pareil sauf que les coefficients stœchiométriques vont se retrouver devant x et xmax !!
On aura donc :
| Etat du système | Avancement | A | + | 3B | → | 4C | + | D |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 | |||
| Etat intermédiaire | x | n0 – x | n1 – 3x | 4x | x | |||
| Etat final | xmax | n0 – xmax | n1 – 3xmax | 4xmax | xmax |
Comme tu le vois rien de bien compliqué, il faut juste rajouter le coefficient devant x et xmax dans la colonne correspondante : pour les réactifs comme pour les produits la règle est la même !
—
ATTENTION ! Les coefficients stœchiométriques se retrouvent uniquement devant x et xmax, PAS devant les quantités de matière initiales n0 et n1 !
—
Prenons un autre exemple pour être sûr que tu as bien compris, avec l’équation suivante :
2A + 5B → C + 3D (amuse toi à trouver tout seul le tableau d’avancement pour t’entraîner  ):
):
| Etat du système | Avancement | 2A | + | 5B | → | C | + | 3D |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 | |||
| Etat intermédiaire | x | n0 – 2x | n1 – 5x | x | 3x | |||
| Etat final | xmax | n0 – 2xmax | n1 – 5xmax | xmax | 3xmax |
Normalement tu devrais avoir trouvé ça 
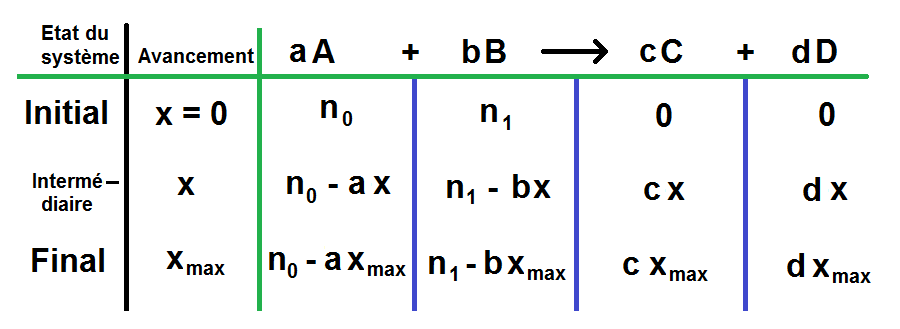
De manière générale, si l’on note a, b, c et d les coefficients stœchiométriques des espèces A, B C et D, on obtient le tableau suivant (a, b c et d sont des chiffres, A, B, C et D sont des espèces chimiques) :
| Etat du système | Avancement | aA | + | bB | → | cC | + | dD |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 | |||
| Etat intermédiaire | x | n0 – ax | n1 – bx | cx | dx | |||
| Etat final | xmax | n0 – axmax | n1 – bxmax | cxmax | dxmax |
Evidemment ce tableau est vrai pour 2 réactifs et 2 produits, mais on peut très bien avoir plus ou moins de réactifs et plus ou moins de produits. Il faudra donc rajouter des colonnes mais elles se rempliront exactement de la même manière que les autres !
Avant de passer aux calculs que l’on peut faire avec ce tableau, parlons un peu de la présentation.
Le tableau d’avancement est comme son nom l’indique… un tableau !
Il faut donc tracer des cases. Oui mais lesquelles, car il y en a beaucoup !
Nous allons nous baser sur le tableau suivant :
Il est conseillé de faire d’abord les deux traits verts.
Ensuite tu écris l’équation.
Puis tu traces les traits bleus sous les + et la flèche de l’équation (ce pourquoi il faut écrire l’équation avant^^).
Enfin tu peux faire le trait noir.
Et c’est tout ! Il ne reste plus qu’à compléter les différentes lignes et colonnes.
On pourrait très bien tracer d’autres traits (pour séparer les lignes et encadrer le tableau par exemple), mais ce n’est pas très utile, et cela va alourdir le tableau déjà bien chargé et prendre du temps supplémentaire.
Bien sûr rien ne t’empêche de faire plus de traits pour bien marquer le tableau, il n’y a pas de règle absolue ce qui a été dit précédemment constitue juste des conseils, à toi de les appliquer à ta manière 
Nous verrons dans les exercices cela de manière encore plus concrète.
Avant de passer à la suite, voyons un exemple avec de vrais chiffres et de vraies espèces chimiques plutôt que des lettres, ce sera plus parlant !
Prenons l’équation C3H8 + 5 O2 → 4 H2O + 3 CO2 (équation vue dans le chapitre sur l’équilibre des réactions).
On suppose que l’on initialement a 2,4 mol de C3H8 et 5,3 mol de O2.
Le tableau d’avancement obtenu est le suivant (essaye de le faire tout seul avant pour t’entraîner !) :
| Etat du système | Avancement | C3H8 | + | 5 O2 | → | 4 H2O | + | 3 CO2 |
| Etat initial (t = 0s) | x = 0 | 2,4 | 5,3 | 0 | 0 | |||
| Etat intermédiaire | x | 2,4 – x | 5,3 – 5x | 4x | 3x | |||
| Etat final | xmax | 2,4 – xmax | 5,3 – 5xmax | 4xmax | 3xmax |
Bon c’est bien joli ce tableau mais à quoi ça sert ??
C’est ce que nous allons voir tout de suite 
Le but du tableau est de décrire l’état du système entre l’instant initial et l’instant final.
Mais le plus important est l’état final du système.
On va donc chercher à compléter la dernière ligne du tableau.
Pour cela il faut donc calculer xmax.
Le principe est le suivant : la réaction va s’arrêter quand un des réactifs aura totalement disparu (puisque à ce moment-là il ne peut plus y avoir de réaction).
On cherche donc à ce que la quantité de matière finale de l’un des réactifs soit égal à 0 mol.
Oui mais lequel ?
Comme on ne sait pas, on va utiliser le fait que la quantité de matière d’un réactif est toujours positive.
Reprenons un tableau de manière générale :
| Etat du système | Avancement | aA | + | bB | → | cC | + | dD |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 | |||
| Etat intermédiaire | x | n0 – ax | n1 – bx | cx | dx | |||
| Etat final | xmax | n0 – axmax | n1 – bxmax | cxmax | dxmax |
D’après ce que l’on a dit précédemment, on se base uniquement sur la quantité de matière finale des réactifs, en disant quel est positive :
0 ≤ n0 – axmax et 0 ≤ n1 – bxmax
d’où xmax ≤ n0/a et xmax ≤ n1/b
On a donc xmax qui doit être plus petit que n0/a et n1/b, on prend donc la plus petite valeur !!!
xmax est donc égal à la plus petite des valeurs trouvées avec le raisonnement que l’on vient de faire.
Prenons un exemple avec des chiffres, à savoir le tableau vue précédemment :
| Etat du système | Avancement | C3H8 | + | 5 O2 | → | 4 H2O | + | 3 CO2 |
| Etat initial (t = 0s) | x = 0 | 2,4 | 5,3 | 0 | 0 | |||
| Etat intermédiaire | x | 2,4 – x | 5,3 – bx | 4x | 3x | |||
| Etat final | xmax | 2,4 – xmax | 5,3 – 5xmax | 4xmax | 3xmax |
Le raisonnement nous donne :
0 ≤ 2,4 – xmax et 0 ≤ 5,3 – 5xmax
xmax ≤ 2,4 et xmax ≤ 5,3/5
On prend alors la plus petite valeur entre 2,4 et 5,3/5 c’est-à-dire 5,3/5 = 1,06 mol.
Comme on doit prendre deux chiffres significatifs, on prend 1,1 mol.
On a donc xmax = 1,1 mol.
Comme tu le vois ce n’est pas si compliqué si tu penses bien à prendre la plus petite valeur : avec de l’entraînement cela deviendra automatique !
Remarque : on a fait ici le cas où l’on a 2 réactifs, donc il faut prendre la plus petite des 2 valeurs trouvées.
Si on a 3 réactifs même principe on prend la plus petite des 3 valeurs, mais au lycée on voit rarement des réactions avec 3 réactifs donc nous ne donnerons pas d’exemple, mais sache que c’est le même principe que l’on ait 2 réactifs ou plus.
Une fois que l’on a trouvé xmax, on peut donner l’état final du système en remplaçant xmax par sa valeur dans la dernière ligne.
Les quantités de matière finales de chaque espèce sont donc :
nC3H8 final = 2,4 – xmax = 2,4 – 1,1 = 1,3 mol
nO2 final = 5,3 – 5xmax = 0 mol
nH2O final = 4xmax = 4 × 1,1 = 4,4 mol
nCO2 final = 3xmax = 3 × 1,1 = 3,3 mol.
A l’état final on a donc :
1,3 mol de C3H8
0 mol de O2
4,4 mol de H2O
3,3 mol de CO2
On voit qu’il n’y a plus de O2 : c’est ce qu’on appelle le réactif limitant.
—
Le réactif limitant est le réactif qui a totalement disparu à la fin de la réaction.
—
Le terme réactif « limitant » vient du fait que c’est la disparition de ce réactif qui arrête la réaction et limite donc la réaction.
Comment trouver ce réactif limitant ?
Tout simplement à partir des inéquations qui servent à calculer xmax !
En effet, pour trouver xmax on a pris la plus petite valeur entre les deux valeurs trouvées grâce aux inéquations.
La plus petite valeur est donc associée à une inéquation elle-même associée à un des réactifs.
Dans notre exemple, on avait 0 ≤ 2,4 – xmax et 0 ≤ 5,3 – 5xmax.
La 1ère inéquation provient de la colonne de C3H8, la 2ème inéquation provient de la colonne de O2.
La valeur retenue pour xmax est 5,3/5 qui provient de la 2ème inéquation, celle liée à O2 : c’est donc O2 le réactif limitant !
Nous réexpliquerons cela bien en détails dans les exercices.
—
Remarque : quand on a calculé nO2 final on a mis directement 0 mol, on n’a pas remplacé xmax par sa valeur qui est 1,1 mol contrairement aux autres espèces.
Pourquoi ? Tout simplement parce que sinon on aurait trouvé 5,3 – 5 × 1,1 = – 0,2 mol : une quantité de matière négative !!
Cela est dû au fait que la valeur de xmax a dû être arrondie à cause des chiffres significatifs.
Mais si on avait pris la vraie valeur de xmax à savoir 5,3/5, on aurait eu 5,3 – 5 × 5,3/5 = 0 mol donc tout est logique !
Ainsi, quand tu sais qui est le réactif limitant, tu peux mettre directement 0 mol pour la quantité de matière finale.
—
Il arrive parfois que les deux réactifs arrivent en même temps à 0 mol, il n’y a donc pas de réactif limitant puisque les deux réactifs ont disparu à la fin de la réaction !
On dit alors que les réactifs ont été introduits dans les proportions stœchiométriques, c’est ce que nous allons détailler maintenant.
Pour expliquer cela nous allons prendre l’équation suivante :
2 Al + 6 H+ → 2 Al3+ + 3 H2
Il faut regarder les coefficients stœchiométriques des réactifs.
On voit qu’ici les coefficients sont 2 et 6 : 6 est le triple de 2.
Pour avoir les proportions stœchiométriques, il faut donc initialement trois fois plus de H+ que de Al.
On peut prendre par exemple 1,0 mol de Al et 3,0 de H+, ou 5,0 mol de Al et 15,0 mol de H+ etc…
En effet, faisons le tableau d’avancement correspondant, on va prendre par exemple 4,0 mol de Al et donc 12,0 mol de H+ :
| Etat du système | Avancement | 2Al | + | 6 H+ | → | 2 Al3+ | + | 3 H2 |
| Etat initial (t = 0s) | x = 0 | 4,0 | 12,0 | 0 | 0 | |||
| Etat intermédiaire | x | 4,0 – 2x | 12,0 – 6x | 2x | 3x | |||
| Etat final | xmax | 4,0 – 2xmax | 12,0 – 6xmax | 2xmax | 3xmax |
Calculons le réactif limitant :
0 ≤ 4,0 – 2xmax et 0 ≤ 12,0 – 6xmax
xmax ≤ 4,0/2 et xmax ≤ 12,0/6
xmax ≤ 2,0 et xmax ≤ 2,0
On trouve la même valeur !!
On a donc xmax = 2,0 mol, et si on calcule la quantité de matière finale des réactifs, on trouve :
nAl final = 4,0 – 2xmax = 0 mol
nH+ final = 12,0 – 6xmax = 0 mol
Ceci est logique puisque les deux réactifs sont « limitants ».
—
ATTENTION !! Ne mélange pas les coefficients stœchiométriques (les chiffres devant les espèces dans les réactions) et les proportions stœchiométriques qui concernent les quantités de matière initiales des réactifs.
—
Pour cet exemple cela était plutôt simple de deviner les proportions puisque 6 est le triple de 2, il faut donc 3 fois de H+ que de Al. Mais quand le lien entre les coefficients stœchiométriques est moins évident, comment fait-on ??
En effet, considérons l’équation suivante :
4 NH3 + 5 O2 → 4 NO + 6 H2O
Les coefficients stœchiométriques des réactifs sont 4 et 5, donc le rapport entre les deux n’est pas évident (pas de double, triple, quadruple etc…)
Prenons donc une équation de manière générale :
| Etat du système | Avancement | aA | + | bB | → | cC | + | dD |
| Etat initial (t = 0s) | x = 0 | n0 | n1 | 0 | 0 | |||
| Etat intermédiaire | x | n0 – ax | n1 – bx | cx | dx | |||
| Etat final | xmax | n0 – axmax | n1 – bxmax | cxmax | dxmax |
Pour que les proportions stœchiométriques soient respectées, on a vu que les deux réactifs devaient avoir disparus à l’état final.
Donc : n0 – axmax = 0 et n1 – bxmax = 0
D’où : n0/a = xmax et n1/b = xmax
On en déduit que :
\(\displaystyle \frac{n_0}{a} = \frac{n_1}{b} \)
—
Ceci est la condition pour que les réactifs aient été introduits dans les proportions stœchiométriques et donc qu’ils aient tous disparus à l’état final.
—
Reprenons le premier exemple :
2 Al + 6 H+ → 2 Al3+ + 3 H2 : ici a = 2 et b = 6.
Si l’on met 3,0 mol de Al et 5,0 mol de H+ (donc n0 = 3,0 mol et n1 = 5,0 mol) :
3,0/2 = 1,5 et 5,0/6 = 0,83 : 1,5 ≠ 0,83 donc les proportions stœchiométriques ne sont pas respectées.
Si l’on met 1,6 mol de Al et 4,8 mol de H+ :
1,6/2 = 0,8 et 4,8/6 = 0,8 : on trouve le même résultat, donc les réactifs ont été introduit dans les proportions stœchiométriques !
Reprenons maintenant l’exemple qui posait problème tout à l’heure :
4 NH3 + 5 O2 → 4 NO + 6 H2O
Si l’on prend 5,2 mol de NH3 et 6,5 mol de O2 :
5,2/4 = 1,3 et 6,5/5 = 1,3 : les réactifs sont en proportions stœchiométriques.
Dans les exemples que l’on vient de voir on avait les quantités initiales de réactifs et on cherchait si les proportions stœchiométriques étaient respectées ou non.
Mais on peut également chercher la quantité d’un des réactifs en connaissant l’autre pour respecter les proportions stœchiométriques !
Avec cette même équation, supposons que l’on ait 3,8 mol de O2. On chercher combien il faudrait mettre de NH3 pour respecter les proportions stœchiométriques.
D’après la formule :
\(\textstyle \frac{n_{NH_3 \, initial}}{4} = \frac{n_{O_2 \, initial}}{5} \)
\(\textstyle n_{NH_3 \, initial} = \frac{4 \times n_{O_2 \, initial}}{5} \)
\(\textstyle n_{NH_3 \, initial} = \frac{4 \times 3,8}{5} \)
\(\textstyle n_{NH_3 \, initial} = 3,04 mol \)
Il faut donc mettre 3,04 mol de NH3 pour avoir un mélange stœchiométrique.
(Remarque : normalement il faudrait mettre 3,0 mol pour respecter les chiffres significatifs, mais ici il s’agit d’une quantité à mettre exactement dans le mélange donc on peut exceptionnellement garder 3,04).
Tu sais maintenant tout sur les tableaux d’avancement, les réactifs limitants et les proportions stœchiométriques.
Sache cependant qu’une réaction n’est pas toujours totale et qu’elle peut s’arrêter alors qu’aucun réactif n’a disparu… On voit cela en Terminale mais ceci fera l’objet d’un autre chapitre ! 
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !



Bonjour,
Merci beaucoup pour ces explications très claires.
Je vais pouvoir faire mes exercices.
Merci beaucoup pour ces explications. Je me retrouve cette année avec une prof qui ne sait pas du tout expliquer son cours et vous me sauvez réellement.
Merci beaucoup, ça m »est très utile !
merci