Sommaire
Équations de désintégrations
Energie libérée par une réaction nucléaire
Energie libérée : défaut de masse en u.a
Pour accéder au cours sur la radioactivité, clique ici !
On considère le Radon radioactif de type α, le plomb Pb radioactif de type β- et le Tantale radioactif de type β+ :
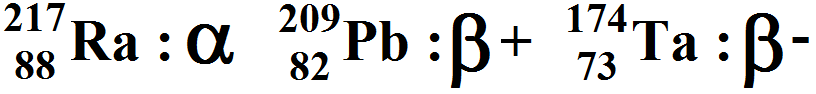
1) Donner les équations de désintégration correspondantes. Quelles particules sont émises ? De quel type de réaction s’agit-il ?
2) Reprendre les même question avec les équations suivantes après avoir trouvé les inconnues :
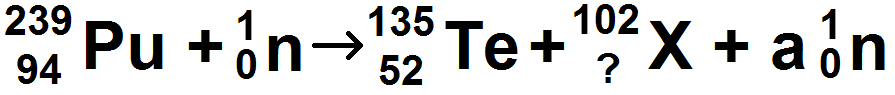
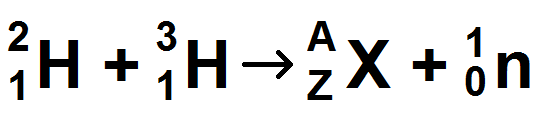
Données : on donne les atomes suivants avec leur numéro atomique :
83Bi, 84Po, 85At, 86Rn, 72Hf, 74W
On considère la réaction de fission ci-dessous :
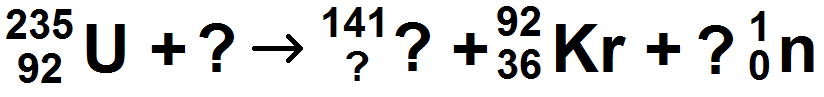
1) Trouver l’énergie libérée après avoir trouvé les inconnus de l’équation (les 4 points d’interrogation).
2) Calculer ensuite l’énergie libérée par 1 kg d’uranium.
Données : célérité de la lumière : 3,00 x 10-8 m.s-1
m(Ba) = 2,33 x 10-25 kg ; m(Kr) = 1,53 x 10-25 kg ; m(n) = 1,67 x 10-27 kg ; m(U) = 3,90 x 10-25 kg
On considère la réaction nucléaire ci-dessous :
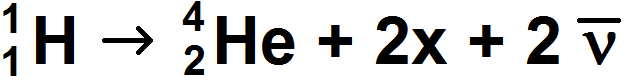
Trouver x puis calculer l’énergie libérée lors de cette réaction.
Données : m(He) = 4,0015 u, m(H) = 1,0073 u, m(x) = 0,55 x 10-3u
1u = 1,66 x 10-27 kg, 1u x c2 = 931,5 MeV.
Retour au coursHaut de la page


