Sommaire
Introduction
Rappels sur les protons, électrons et neutrons
Radioactivité α, β +, β – et γ
Diagramme de stabilité / de Ségré
Réactions nucléaires provoquées : fusion et fission
Bilan de masse et d’énergie
Défaut de masse et énergie de liaison
Loi de décroissance radioactive
Activité radioactive
Exercices
La radioactivité est le phénomène physique par lequel des noyaux atomiques instables se transforment spontanément en d’autres noyaux, en émettant simultanément des particules de matière (électrons, neutrons, etc… ).
Autrement dit, il s’agit d’une transformation avec initialement 1 ou plusieurs noyaux, et à la fin d’autres noyaux et des particules.
Mais attention, contrairement aux équations chimiques, il n’y aura pas conservation des noyaux ! Les règles seront en effet différentes de celles vues dans le chapitre sur les réactions chimiques.
Il ne s’agit pas non plus d’une transformation physique comme une évaporation, une fusion ou une condensation par exemple.
Nous verrons donc les règles s’appliquant aux différents types de transformations radioactives (appelées désintégrations) après avoir fait un rappel sur les bases des atomes (protons, neutrons, électrons etc…)
Nous verrons également l’aspect mathématique de la radioactivité avec la loi de décroissance radioactive, très utilisée dans les exercices.
Avant de lire ce qui suit, tu es fortement invité à lire (ou relire) le chapitre sur les atomes.
Nous allons résumer ci-dessous ce qu’il est important de retenir dans ce chapitre pour la bonne compréhension du chapitre sur la radioactivité.
Un atome est constitué d’un noyau contenant des protons et des neutrons. Ces particules sont appelés des nucléons.
Autour de ce noyau gravitent des électrons selon le schéma suivant :
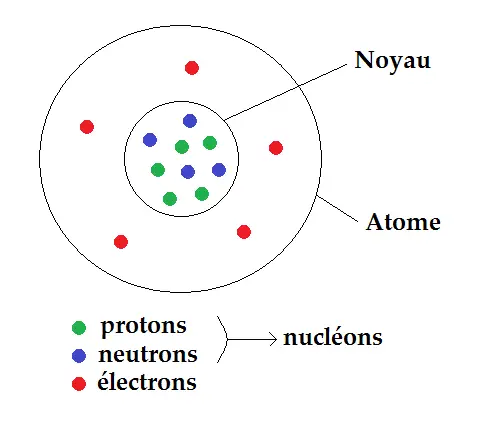
Les protons ont une charge électrique positive (charge élémentaire +e = 1,6 x 10-1 C), celle des électrons est négative (-e), celle des neutrons est nulle (0 C).
Le nombre de protons est noté Z, appelé numéro atomique, celui des nucléons A, appelé nombre de masse.
Donc nombre de neutrons = A – Z.
L’atome étant neutre, il y a autant de protons que d’électrons, donc il y a Z électrons.
Un atome X aura la notation suivante :

Z est appelé numéro atomique car c’est ce nombre qui définit à quel atome cela correspond.
Donc à chaque atome correspond un Z et réciproquement.
Ainsi, comme Z = 6 correspond au carbone, tous les carbone auront un Z qui vaut 6. Et si Z = 6 c’est forcément un carbone, ça ne peut pas être de l’oxygène par exemple !
Par contre il n’y a aucune règle sur le A, il peut être différent pour un même atome.
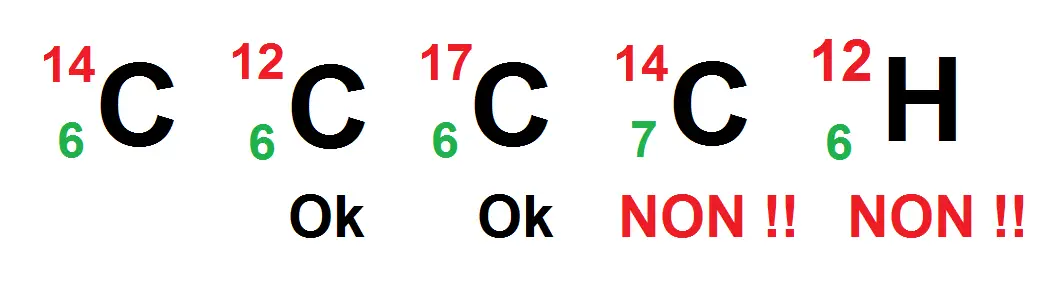
L’avant-dernier n’est pas possible car l’atome est du carbone, donc son Z vaut forcément 6, or là il vaut 7.
Le dernier n’est pas possible car le Z = 6, donc c’est forcément du carbone, or le symbole est celui de l’hydrogène.
Tu vois que le A n’intervient absolument pas dans ce type de raisonnement, il peut prendre différentes valeurs indépendamment de l’atome en question contrairement au Z.
Par contre, les trois premiers ont le même Z mais pas le même A, c’est ce qu’on appelle des isotopes.
—
Des isotopes sont des atomes qui ont le même numéro atomique mais pas le même nombre de masse (même Z mais pas même A).
—
Les isotopes seront omniprésents dans ce chapitre sur la radioactivité.
Nous allons considérer ici principalement des noyaux et non des atomes, ce qui revient presque au même, c’est juste que l’on ne prend pas en compte les électrons qui gravitent autour du noyau.
Les noyaux seront notés de la même manière que les atomes.
Les rappels étant terminés, nous allons pouvoir passer au cœur du sujet ! 
Il existe trois grands types de radioactivité : α, β + et β -. La radioactivité γ (gamma) est un peu différente.
Dans chaque cas, on partira d’un noyau X, et on aura en produit un autre atome Y, une particule (particule α, particule β + et particule β -), et éventuellement autre chose.
Avant de détailler chaque type, il faut que tu connaisses les lois de Soddy, qui sont des lois traduisant la conservation du nombre de nucléons et celle de la charge (conservation des A et des Z).
Ainsi, supposons que l’on ait :
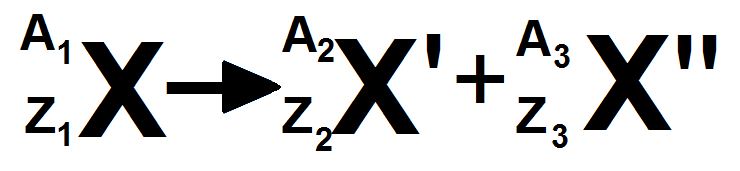
X, X’ et X " sont des noyaux.
On peut dire d’après les lois de Soddy que :
\(\displaystyle A_1 = A_2 + A_3 \)
\(\displaystyle Z_1 = Z_2 + Z_3 \)
Bien sûr cela marche avec autant de noyaux et particules que l’on veut.
Nous verrons à quoi servent ces lois.
Détaillons maintenant chaque type de désintégration.
1) La désintégration α (alpha)
La désintégration α correspond à l’émission d’une particule α qui est un noyau d’hélium.
—
Attention, c’est un noyau d’hélium et non un atome d’hélium, donc il y a uniquement des protons et des neutrons dans α, pas d’électrons.
—
Dans un noyau d’hélium il y a 2 protons et 2 neutrons, donc une particule α se note :
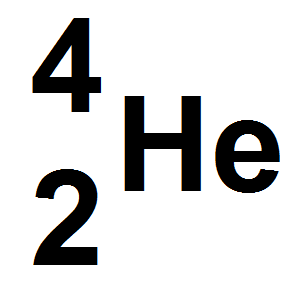
—
Attention, même s’il s’agit d’un noyau d’hélium et non d’un atome d’hélium, la notation est la même, mais cela n’a aucune incidence sur la suite du raisonnement.
—
On trouve aussi la notation :
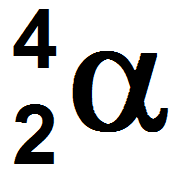
L’équation d’une désintégration α est donc :
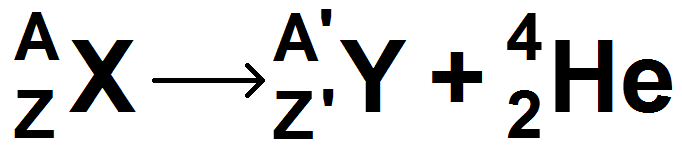
Mais quel est le numéro atomique de Y et son nombre de neutrons ??
Pour le savoir, il suffit d’appliquer les lois de Soddy, grâce auxquelles on peut écrire :
A = A’ + 4
Z = Z’ + 2
D’où :
A’ = A – 4
Z’ = Z – 2
On en déduit que :
—
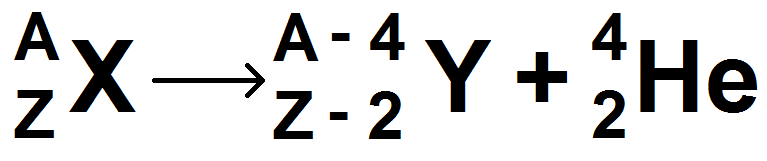
Équation d’une désintégration α
—
Z – 2 signifie que le noyau perd 2 protons.
A – 4 signifie que le noyau perd 4 nucléons : comme il perd 2 protons, il perd aussi 2 neutrons.
Ainsi au cours d’une désintégration de type α, un noyau perd 2 protons et 2 neutrons.
Voyons un exemple.
On suppose que le carbone 14 suit une désintégration de type α, on demande d’écrire l’équation correspondante. On écrit donc :
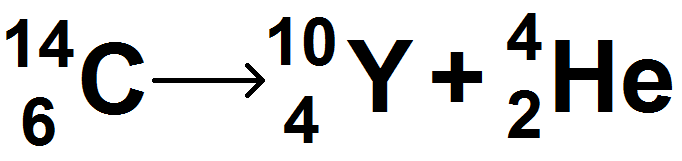
Pour savoir à quoi correspond Y, il faut regarder son Z, qui vaut 4, qui d’après le tableau périodique correspond à Be.
On a donc :
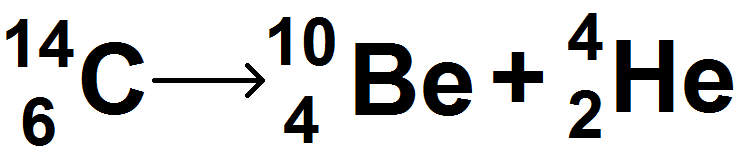
Comme tu le vois c’est très simple ! 
2) La désintégration β + (béta plus)
La désintégration β + correspond à l’émission d’une particule β +, qui est un positron.
—
Un positron est une particule de même masse qu’un électron, mais de charge opposée, donc +e, c’est-à-dire la même charge qu’un proton.
Attention à ne pas confondre avec un proton, qui est beaucoup plus lourd qu’un électron et donc qu’un positron.
—
Un positron ayant la même charge qu’un proton mais n’étant pas un proton, il se note :
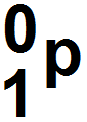
Par ailleurs, la désintégration β + s’accompagne de l’émission d’une particule appelée neutrino, particule élémentaire neutre et de masse nulle qui se note ν (lettre grecque « nu » qui ressemble à un « v ») :
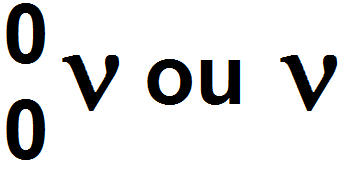
L’équation s’écrit donc :
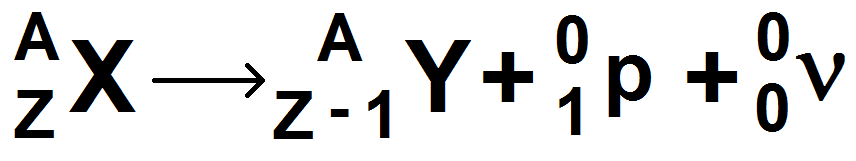
On voit aisément que les lois de Soddy sont vérifiées.
Z – 1 traduit le fait que le noyau X a perdu un proton. Mais il y a le même nombre de nucléons (même A), cela signifie qu’il y a un neutron en plus !
En fait, il y a un proton qui s’est transformé en neutron. La charge électrique perdue lors de ce changement est récupérée par le positron, il y a donc bien conservation de la charge.
3) La désintégration β – (béta moins)
La désintégration β – est similaire à la β +, sauf qu’une particule β – correspond à un électron.
La désintégration s’accompagne de l’émission d’un anti-neutrino et non d’un neutrino. Il se note comme un neutrino mais avec une barre au-dessus (pour signifier que c’est l’antiparticule du neutrino) :
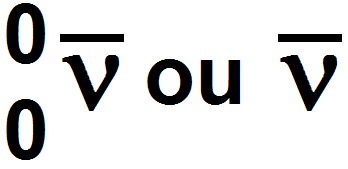
L’équation s’écrit :
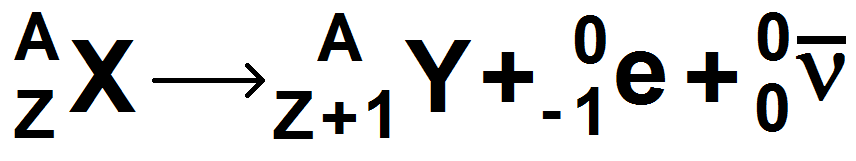
A l’inverse de β +, on voit aisément qu’un neutron se transforme un proton : il y a création d’une charge, et pour compenser une charge négative apparaît : l’électron. Ainsi la conservation de la charge est bien respectée.
4) La désintégration γ (gamma)
En plus de ces 3 désintégrations, il existe une désintégration particulière : la désintégration gamma.
On avait vu dans le chapitre sur les niveaux d’énergie que les atomes peuvent se trouver non pas dans leur état fondamental mais dans un état excité, et il se désexcite en émettant un photon.
Il en est de même pour les noyaux !
Un noyau excité se note avec une étoile (par exemple C*).
Ce noyau peut se désexciter pour donner le même noyau (mais non excité), en émettant un photon γ, particule de masse et de charge nulle.
L’équation est donc :
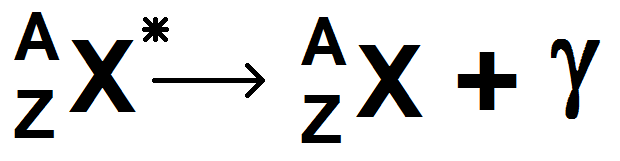
Là encore les lois de Soddy sont évidemment vérifiées.
Nous verrons dans les exercices en vidéo comment manipuler ces désintégrations.
Le diagramme de stabilité, aussi appelé diagramme de Ségré, permet de savoir quel type de désintégration subit un noyau selon son nombre de protons et de neutrons.
On réalise un diagramme avec le nombre de protons Z en abscisse, et le nombre de neutrons N en ordonnée. On aboutit à cela :
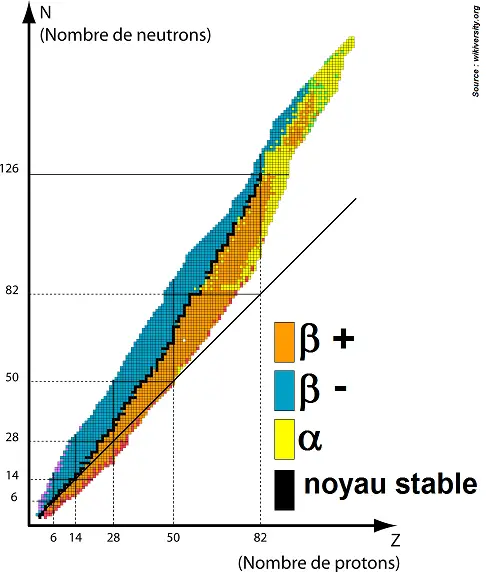
On voit qu’il y a peu de noyaux stables (en noir). Ils constituent une zone de stabilité vers laquelle vont tendre les noyaux lors des désintégrations car ils cherchent à devenir stables.
En effet, la zone au-dessus, en bleu, correspond à des désintégrations β – : normal car lors de cette désintégration, un neutron se transforme en proton, le noyau va donc se décaler d’une case en bas (perte d’un neutron) et d’une case vers la droite (gain d’un proton), et ainsi se rapprocher de la zone de stabilité.
A l’inverse, la zone en-dessous, en orange, correspond à β + : lors de cette désintégration, un proton se transforme en neutron, le noyau va donc se décaler d’une case en haut (gain d’un neutron) et d’une case vers la gauche (perte d’un proton), et ainsi se rapprocher de la zone de stabilité.
En jaune, les noyaux sont trop éloignés de la zone de stabilité et vont donc perdre des protons et des neutrons (2 protons et 2 neutrons qui vont constituer la particule α).
Toutes les désintégrations que l’on vient de voir se font naturellement car le noyau est instable, il se désintègre tout seul.
Mais certaines réactions nucléaires se font suite à un choc entre deux noyaux ou entre un noyau et une particule, ce que l’on fait par exemple dans les centrales nucléaires : on les appelle des réactions nucléaires provoquées.
Dans le cas de réactions nucléaires provoquées, on ne parle plus de désintégration.
Les principales réactions nucléaires provoquées que l’on étudie sont la fusion et la fission nucléaire.
Lors de ces réactions, les lois de Soddy sont bien évidemment vérifiées.
Commençons par la fission nucléaire.
Au cours de cette réaction, un noyau lourd est bombardé par un neutron. Sous l’impact du choc, le noyau lourd se scinde en deux noyaux plus légers et des neutrons sont libérés.
Ces neutrons libérés peuvent à leur tour provoquer la fission d’autres noyaux lourds, ce qui provoque une réaction en chaîne.
A chaque réaction de l’énergie est libérée, et comme la réaction se fait en chaîne, une quantité importante d’énergie peut être libérée, c’est pourquoi on utilise ce procédé dans les centrales nucléaires.
Un exemple très classique est la fission de l’uranium 235 :
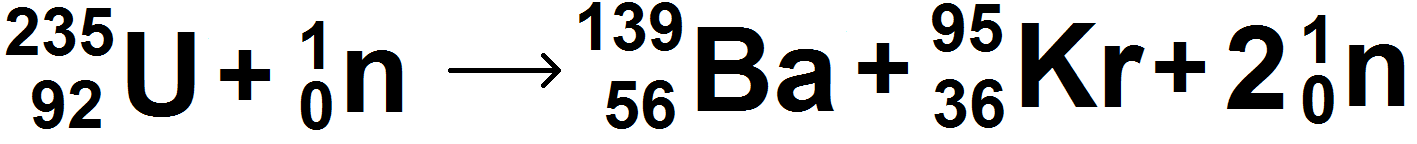
On peut le schématiser de la manière suivante :
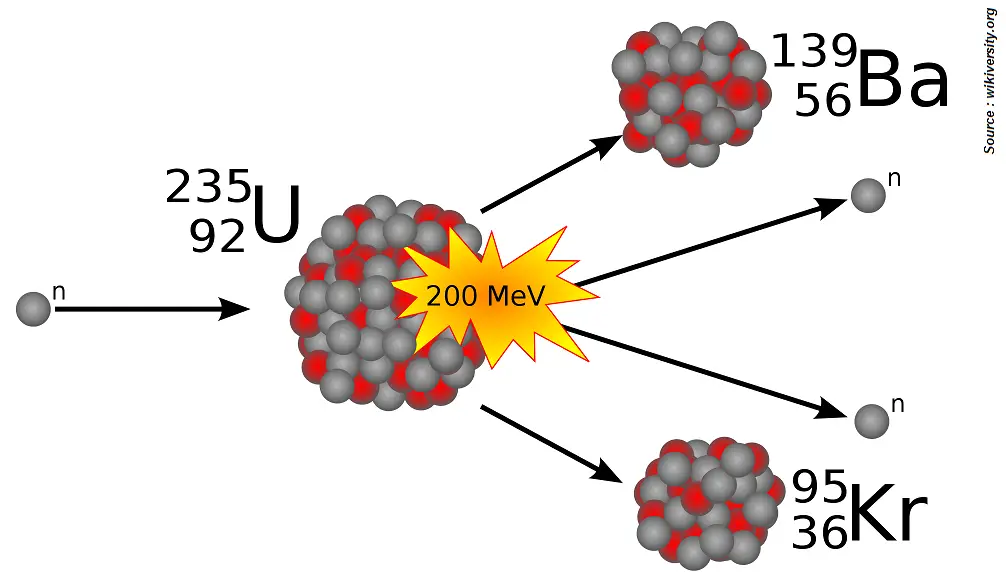
Les boules grises représentent les neutrons, les rouges les protons.
On parle de noyau « lourd » car il contient suffisamment de protons et de neutrons pour se séparer en deux autres noyaux.
Un noyau lourd est dit fissible, car il peut subir une fission nucléaire.
A l’inverse, une fusion nucléaire correspond au regroupement de deux noyaux légers pour donner un noyau plus lourd.
Dans ce cas, pas besoin de bombarder initialement par un neutron.
En revanche, des neutrons peuvent apparaître avec le noyau lourd.
Exemple :
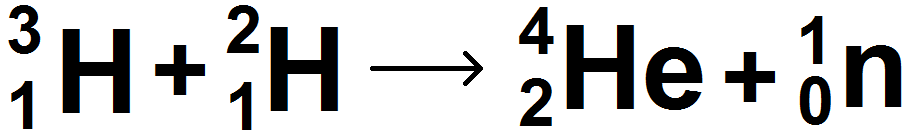
Là encore on peut le schématiser de la manière suivante :
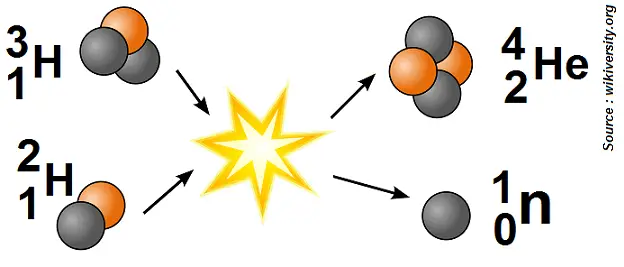
Les boules grises représentent les neutrons, et les orange les protons.
Remarque : avec ce schéma on voit bien la conservation des neutrons et des protons, puisqu’il y a autant de boules grises à gauche qu’à droite, et idem pour les boules orange : les lois de Soddy sont vérifiées !
La fusion nucléaire dégage beaucoup plus d’énergie que la fission mais n’est pas aussi bien maîtrisé par l’Homme (pour l’instant !).
Des fusions nucléaires ont lieu naturellement dans les étoiles comme le Soleil par exemple.
Nous allons maintenant parler d’énergie et de masse.
En effet, au cours d’une désintégration nucléaire, la masse n’est pas constante, elle varie, c’est ce que l’on appelle le défaut de masse.
Cette différence de masse, notée Δm, va conduire à une énergie par la relation très connue d’Einstein :
\(\displaystyle E = \Delta m \, c^2 \)
Ici E est en Joules, Δm en kg et c en m.s-1.
c est la célérité de la lumière dans le vide, on prend souvent c = 3,00 x 108 m.s-1.
Ce qui nous intéresse c’est surtout la variation entre l’état initial et l’état final, donc on va plutôt considérer la formule :
\(\displaystyle \Delta E = \Delta \, m c^2 \)
\(\displaystyle \Delta m = m_{finale} – m_{initiale} \)
—
Attention, il est possible que tu vois l’inverse, à savoir Δm = masse initiale – masse finale.
Cela change juste le signe de E et l’interprétation de ce signe.
—
Bien sûr la masse finale est la somme de masses des différentes entités présentes à l’état final.
Exemple :
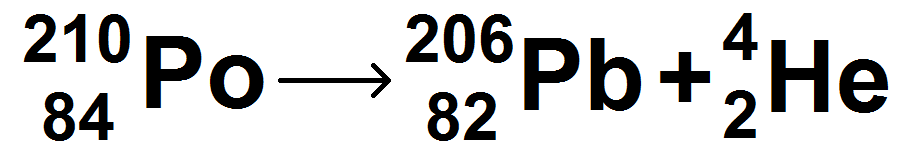
\(\textstyle \Delta m = (m_{Pb} + m_{He}) – (m_{Po}) \)
Lors d’une réaction spontanée (de type α, β + ou β -), Δm sera toujours strictement positif.
Dans ce que l’on vient de décrire, la masse est en kg. Mais dans ce chapitre, elle sera souvent donnée en u.m.a dans les exercices.
u.m.a signifie unité de masse atomique, elle est souvent notée simplement u.
Quel est l’intérêt de u ?
Comme les masses des noyaux et des particules sont souvent faibles (ordre de grandeur 10-27 kg), on a décidé de créer une unité plus appropriée.
Par définition :
\(\displaystyle 1 u = \frac{1}{N_A} (en \, g) \)
Dans cette formule, NA est le nombre d’Avogadro, et u est exprimé en grammes (g).
Si tu fais le calcul, et que l’on convertit en kg, tu trouveras que
\(\displaystyle 1 u = 1,66056 \times 10^{-27} kg \)
On retrouve ainsi l’ordre de grandeur des masses des noyaux.
Par ailleurs, l’énergie est souvent exprimée en eV et non en Joules comme on l’avait vu dans le chapitre sur les niveaux d’énergie.
Comme on multiple la masse à chaque fois par c2 pour avoir l’énergie, ce qui nous intéresse c’est comment passer directement de la masse en u à l’énergie en eV.
Calculons donc l’énergie correspond à 1 u :
\(\textstyle E = 1,66056 \times 10^{-27} \times (2,998 \times 10^8)^2 \)
\(\textstyle E = 1,4925 \times 10^{-10} J \)
On convertit en eV :
\(\textstyle E = \frac{1,4925 \times 10^{-10}}{1,6 \times 10^{-19}} eV \)
\(\displaystyle E_{(1 \, u)} = 931,5 MeV \)
—
Ainsi, pour passer de u à MeV, il suffit de multiplier par 931,5 !!
—
On écrit également
\(\displaystyle u \times c^2 = 931,5 MeV \)
—
Pour récapituler : quand on a Δm et que l’on veut calculer l’énergie correspondante, soit on applique la formule ΔE = Δm × c2, avec la masse en kg et l’énergie en Joules, soit on applique la formule ΔE = Δm × 931,5 avec la masse en u et l’énergie en MeV.
—
Nous ferons des applications dans les exercices en vidéo.
Voyons maintenant l’énergie de liaison qui est souvent utilisée en exercices.
La masse d’un noyau est due à la masse des protons et des neutrons qui composent le noyau au repos.
Mais il y a une petite subtilité : quand les protons et les neutrons ne sont pas regroupés pour former un noyau, leur masse est légèrement supérieure.
Ainsi, la masse des protons et des neutrons isolés est supérieure à celle de ces mêmes protons et neutrons regroupés dans un noyau.
Comme il y a Z protons et A – Z neutrons, cela s’écrit :
\(\textstyle Zm_p + (A – Z)m_n \, \gt \, m_{noyau} \)
mp est la masse d’un proton et mn la masse d’un neutron.
On peut aussi l’écrire :
\(\textstyle Zm_p + (A – Z)m_n – m_{noyau} \, \gt \, 0 \)
Cette quantité positive est appelée le défaut de masse et notée Δm.
On a donc :
\(\textstyle \Delta m = Zm_p + (A – Z)m_n – m_{noyau} \, \gt \, 0 \)
A partir de ce Δm on peut évidemment calculer l’énergie correspondante avec ΔE = Δm c2.
Cette énergie est appelée énergie de liaison, et notée El :
\(\displaystyle E_l = \Delta m \times c^2 \)
énergie de liaison
Or, comme Δm correspond à la masse finale – masse initiale, cela revient à faire une transformation avec initialement un noyau, et à la fin les protons et les neutrons séparés.
Autrement dit :
—
L’énergie de liaison est l’énergie qu’il faut fournir à un noyau au repos pour le dissocier en nucléons isolés et immobiles.
—
Comme le défaut de masse Δm est positif, cette énergie est positive : normal car le système initial (le noyau) reçoit cette énergie pour pouvoir se dissocier en nucléons isolés.
A partir de cette énergie de liaison, on peut calculer l’énergie de liaison par nucléon, obtenue comme son nom l’indique en divisant l’énergie de liaison d’un noyau par le nombre de nucléons (noté A) composant ce noyau :
\(\displaystyle \frac{E_l}{A} \)
Elle peut s’exprimer en Joule/nucléon mais s’exprime généralement en Mev/nucléon.
Si on trace la courbe des énergies de liaison par nucléon pour chaque atome en fonction du nombre de nucléons, on obtient ce que l’on appelle la courbe d’Aston :
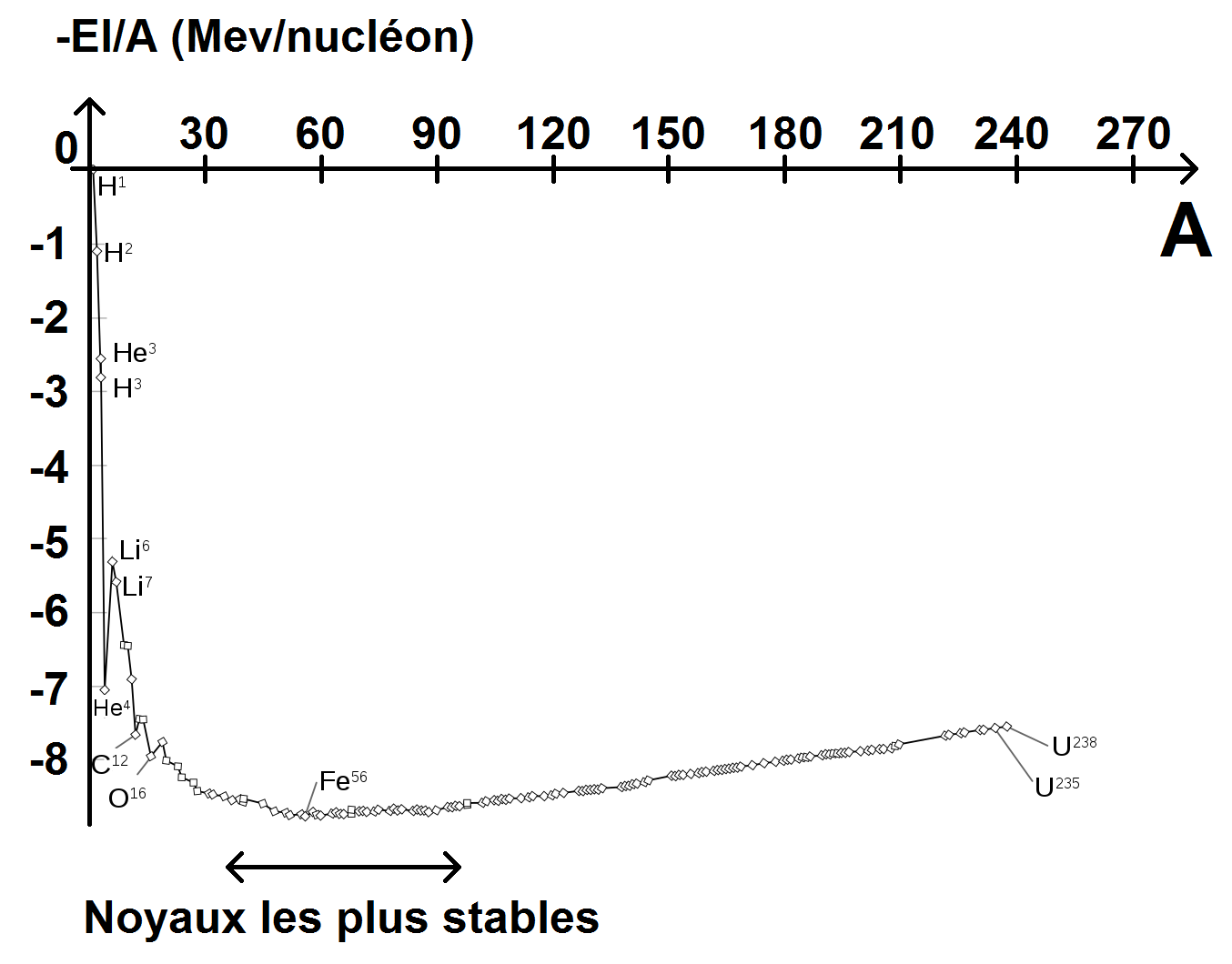
Tu auras remarqué que l’on trace en fait -El/A en fonction de A et non El/A afin d’avoir un point de stabilité en bas (comme une cuvette). En effet, la zone située autour de A = 70 est une zone de stabilité : les noyaux vont chercher à se rapprocher de cette zone.
Ceux qui sont à gauche vont plutôt faire de la fusion nucléaire (afin d’augmenter leur masse et donc leur A) : il s’agit de noyaux légers.
Ceux qui sont à droite vont plutôt faire de la fission nucléaire (afin de diminuer leur masse et donc leur A) : il s’agit de noyaux lourds.
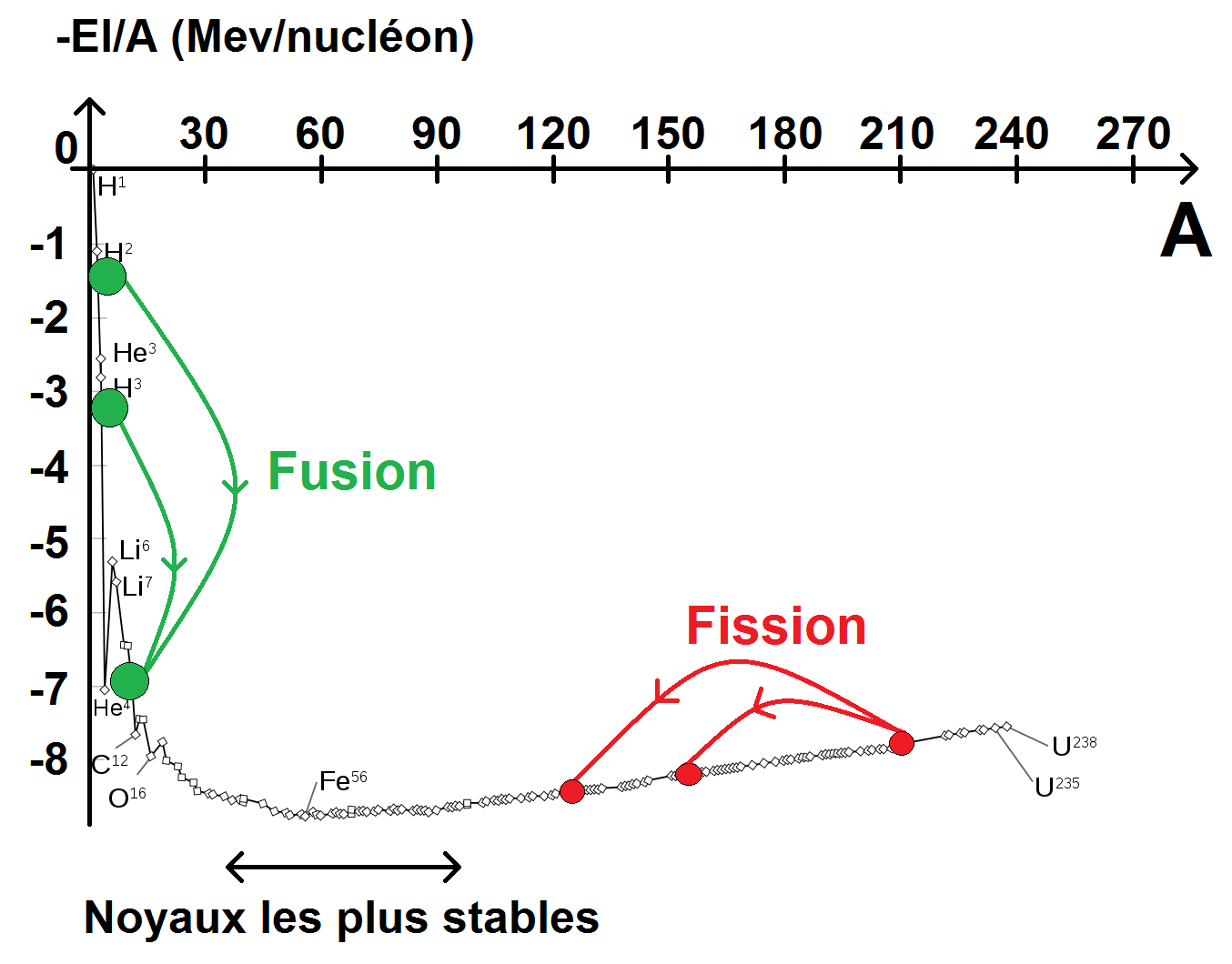
Chaque noyau va en fait chercher à se rapprocher de la zone de stabilité, par fusion ou par fission suivant qu’il soit situé à droite ou à gauche de cette zone.
L’autre intérêt de l’énergie de liaison est de calculer plus facilement l’énergie correspondante à une réaction.
En effet, considérons la réaction suivante :
\(\textstyle X_1 + X_2 \rightarrow X_3 + X_4 \)
Pour calculer l’énergie libérée pendant cette transformation, 2 méthodes :
Soit on utilise la formule de base ΔE = Δm × c2 :
\(\textstyle \Delta E = [m(X_4) + m(X_3) – m(X_1) – m(X_2)] \times c^2 \)
Soit on utilise les énergies de liaisons : ΔE = ΔEl = El(finale) – El(initiale) :
\(\textstyle E = E_l(X_4) + E_l(X_3) – E_l(X_1) – E_l(X_2) \)
Suivant ce que l’on te donne dans l’exercice tu utiliseras plus l’une ou l’autre des deux formules.
Nous verrons en exercices les différentes questions que l’on peut te poser sur l’énergie et la masse.
Passons maintenant à la loi de décroissance radioactive.
On considère un échantillon contenant plusieurs noyaux radioactifs.
On cherche à savoir le nombre de noyaux désintégrés et ceux qui ne le sont pas encore à un instant t quelconque.
Pour cela, on va introduire une constante radioactive λ correspondant à la probabilité pour un noyau de se désintégrer par unité de temps.
Une probabilité étant sans unité, on en déduit que :
—
La constante radioactive λ est en s-1.
—
On va considérer deux instants : t et t + dt, dt étant une période infinitésimale.
On note N(t) le nombre de noyaux non désintégrés à l’instant t, N(t+dt) le nombre de noyaux non désintégrés à l’instant t+dt.
Par définition de λ, la probabilité pour qu’un noyau se désintègre pendant la période dt est λ dt.
Comme il y a N(t) noyaux au début de cette période, le nombre de noyaux s’étant désintégrés pendant cette période dt est N(t) λ dt.
De plus, le nombre de noyaux s’étant désintégrés est N(t) – N(t + dt) qui vaut -dN (car il y a plus de noyaux avant qu’après).
On en déduit que :
N(t) – N(t + dt) = N(t) λ dt
-dN = N(t) λ dt
Ainsi :
\(\textstyle \frac{dN}{dt} = – \lambda N(t) \)
On vient de faire apparaître une équation différentielle de style y’ = ay, avec a = -λ.
On en déduit :
\(\textstyle N(t) = ke^{-\lambda t} \)
En notant N0 le nombre de noyaux initial, on obtient :
\(\displaystyle N(t) = N_0 \, e^{-\lambda t} \)
Cette expression est à connaître par cœur, mais tu peux aussi retenir la démonstration permettant d’obtenir cette relation 
Si on trace cette courbe, on obtient :
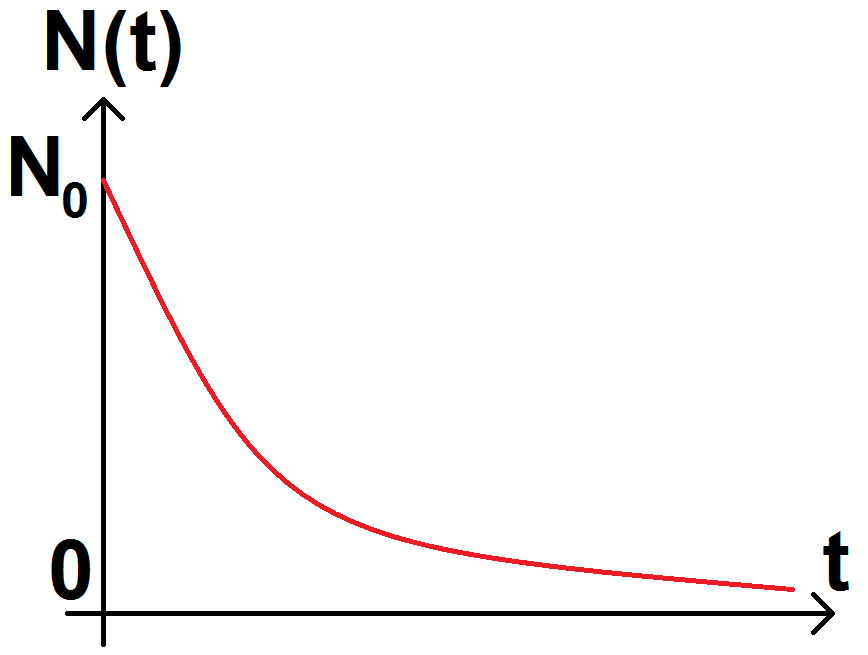
On définit alors le temps de demi-vie, noté t1/2, correspondant au temps au bout duquel il ne reste plus que la moitié des noyaux initialement présents (c’est-à-dire que la moitié des noyaux s’est désintégrée).
On a alors :
\(\textstyle N(t_{1/2}) = \frac{N_0}{2} \)
Cherchons l’expression de t1/2 :
\(\textstyle N_0 e^{-\lambda t_{1/2}} = \frac{N_0}{2} \)
\(\textstyle e^{-\lambda t_{1/2}} = \frac{1}{2} \)
\(\textstyle -\lambda t_{1/2} = ln(\frac{1}{2}) \)
\(\textstyle \lambda t_{1/2} = ln(2) \)
\(\displaystyle t_{1/2} = \frac{ln(2)}{\lambda} \)
Cette formule est également à savoir par cœur !!
On vérifie aisément qu’elle est bien homogène, puisque λ est en s-1.
Remarque : le temps de demi-vie est parfois appelé période radioactive et noté T.
Il existe une propriété importante à retenir : tous les t1/2, la moitié des noyaux se désintègre.
C’est-à-dire qu’au bout de t1/2, il reste N0/2 noyaux.
Au bout 2 t1/2, il reste N0/4 noyaux.
Au bout 3 t1/2, il reste N0/8 noyaux.
Au bout 4 t1/2, il reste N0/16 noyaux.
Etc…
Au bout nt1/2, il reste N0/2n noyaux.
Graphiquement, cela donne :
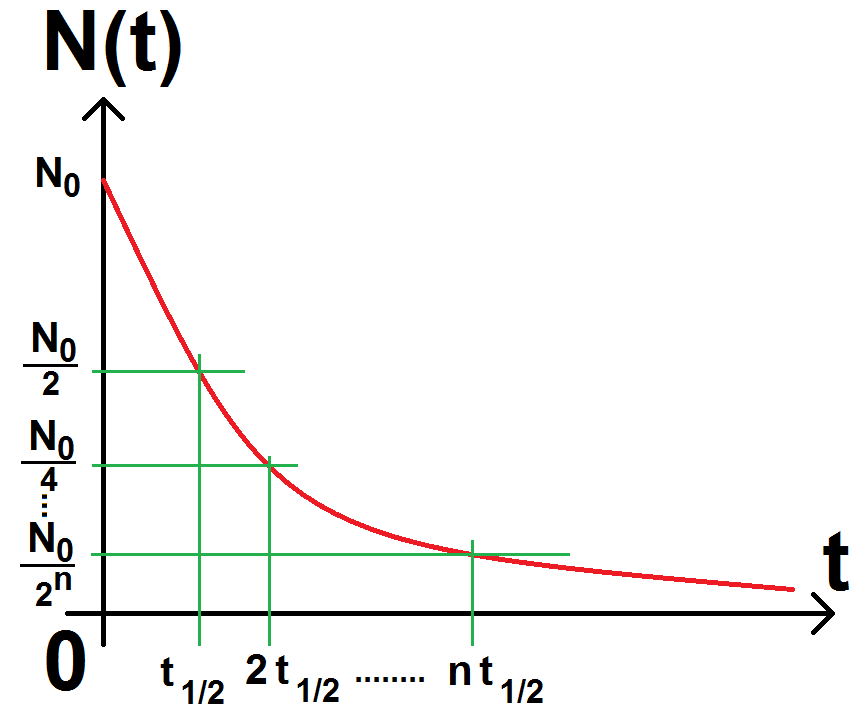
La démonstration mathématique est simple : on considère l’instant nt1/2.
\(\textstyle nt_{1/2} = n\frac{ln(2)}{\lambda} \)
\(\textstyle nt_{1/2} = \frac{ln(2^n)}{\lambda} \)
Calculons le N correspondant :
\(\textstyle N(nt_{1/2}) = N_0e^{- \lambda \frac{ln(2^n)}{\lambda}} \)
\(\textstyle N(nt_{1/2}) = N_0e^{-ln(2^n)} \)
\(\textstyle N(nt_{1/2}) = \frac{N_0}{e^{ln(2^n)}} \)
\(\textstyle N(nt_{1/2}) = \frac{N_0}{2^n} \)
Cette formule explique bien le principe énoncé précédemment.
Dans la vie courante, la radioactivité ne se mesure pas en nombre de noyaux, mais en nombre de désintégrations par unité de temps, aussi appelé Becquerel, noté Bq.
Un nombre de désintégrations étant sans unité, on en déduit que le Bq correspond à des s-1 :
1 Bq = 1 désintégration par seconde.
C’est ce que l’on appelle l’activité d’un échantillon, noté A(t).
—
L’activité d’un échantillon radioactif, notée A(t), correspond au nombre de désintégrations par seconde.
L’unité est le Bq (Becquerel) : 1 Bq = 1 désintégration par seconde.
—
Par définition de la constante radioactive λ on a :
\(\displaystyle A(t) = \lambda N(t) \)
En remplaçant :
\(\textstyle A(t) = \lambda N_0 e^{- \lambda t} \)
λ N0 correspond à l’activité de l’échantillon à l’instant t = 0, on la note souvent A0, d’où :
\(\displaystyle A(t) = A_0 \, e^{- \lambda t} \)
A0 est l’activité initiale de l’échantillon
L’activité suit donc la même loi de décroissance radioactive que N(t), donc il y a les mêmes propriétés (t1/2, etc…), ce qui est normal puisque A(t) et N(t) sont proportionnels (A(t) = λ N(t)).
Selon les exercices, on raisonnera soit sur N(t), soit sur A(t), soit sur les deux, tout dépendra des exercices !
Le chapitre étant justement terminé, il est temps de passer aux exercices en vidéo 
Pour accéder aux exercices sur ce chapitre, clique ici !
Sommaire des coursHaut de la page


