Sommaire
Introduction
Représentation de Cram
Objet chiral ou non
Carbone asymétrique
Stéréoisomères de configuration
Avec 2 carbones asymétriques
Diastéréoisomères Z / E
Stéréoisomères de conformation
Exercices
Dans ce chapitre nous allons voir les stéréoisomères, à ne pas confondre avec les isomères.
On rappelle que les isomères sont des molécules de même formule brute mais de formule semi-développée différente.
Les stéréoisomères ont même formule brute, même formule semi-développée, mais leur agencement dans l’espace est différent, ce qui modifie les propriétés de la molécule notamment.
Nous apprendrons à identifier les différents types de stéréoisomères.
Puisque leur agencement dans l’espace diffère, il faut trouver une manière de représenter ces différents agencements : c’est ce que l’on appelle la représentation de Cram.
La représentation de Lewis permet de représenter les liaisons entre les molécules, mais toutes ces liaisons sont dans un même plan (celui de la feuille), alors que les molécules ne sont pas toutes en 2D, beaucoup sont en 3D.
La représentation de Cram permet de représenter cette 3ème dimension.
Les traits « normaux » représentent toujours les liaisons dans le plan, tandis que des triangles pleins représentent des liaisons « devant », c’est-à-dire qui viennent vers l’observateur, tandis que des triangles en traits représentent des liaisons « derrière », c’est-à-dire qui s’éloignent de l’observateur.
Prenons un exemple :
Imaginons un observateur qui regarde la molécule conformément à la flèche.
L’atome vert (A) lui paraîtra devant, la liaison sera donc représentée par un triangle plein.
L’atome noir (B) lui paraîtra derrière, la liaison sera donc représentée par un triangle en traits.
L’atome blanc (C) lui paraîtra en haut mais dans le plan vertical, il sera en trait normal.
L’atome violet (D) lui paraîtra à droite mais dans le plan vertical, il sera en trait normal.
La molécule en représentation de Cram sera donc :
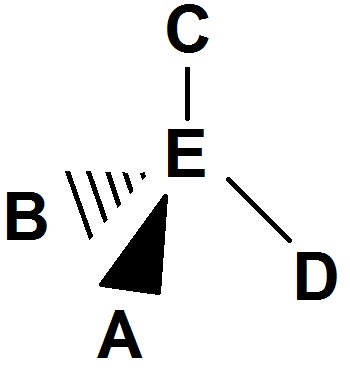
Attention, on peut également avoir un autre point de vue, et alors la molécule aura une représentation de Cram différente.
Si par exemple un observateur se trouve derrière, on aura :
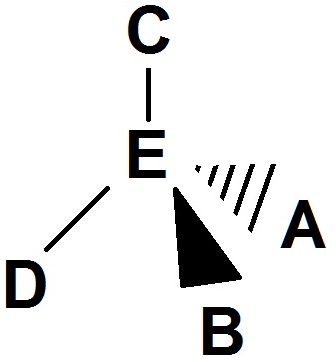
Il s’agit de la même molécule que précédemment, on l’a juste « retournée » (on l’a faite pivoter autour d’un axe vertical imaginaire).
Autre exemple plus compliqué (mais qu’on rencontrera souvent) :
Imaginons un observateur qui regarde la molécule avec les 2 atomes verts face à lui conformément à la flèche.
Les atomes A et F étant face à lui, les liaisons seront des triangles pleins.
Les atomes B et D étant derrière, les liaisons seront des triangles en traits.
L’atome C en haut à gauche et le E en haut à droite dans le plan vertical : ils seront en traits normaux.
Les atomes G et H sont dans le plan vertical, la liaison entre ces deux atomes est aussi dans le plan, donc elle sera en trait normal :
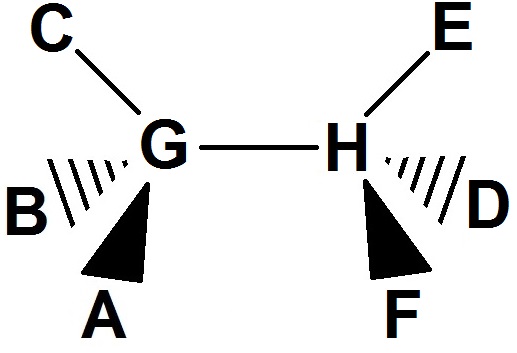
Tu entendras peut-être parler de disposition tétraédrique : un tétraèdre est une pyramide à base triangulaire.
Supposons que l’on ait la molécule suivante (on a mis un carbone au centre car ce sera presque toujours le cas par la suite) :
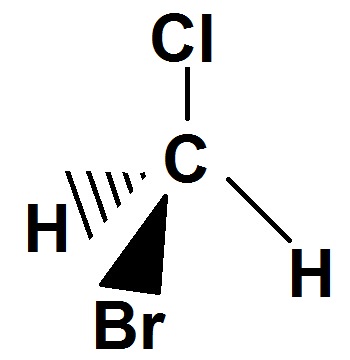
En fait, c’est comme si le carbone était au centre du tétraèdre et que les 4 atomes reliés au carbone étaient sur les sommets du tétraèdre (le tétraèdre est représenté en rouge) :
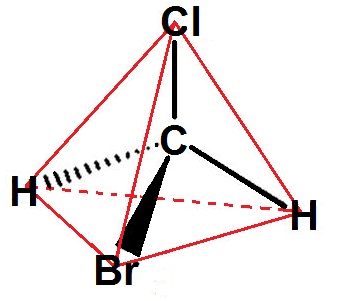
Nous allons maintenant introduire un nouveau mot : la chiralité.
Un objet quelconque peut être chiral ou non chiral (on dit achiral). Pour le savoir, il faut le placer devant un miroir :
– si l’image est superposable (c’est-à-dire identique), l’objet n’est pas chiral.
– si l’image n’est pas superposable (donc différente), l’objet est chiral.
—
Un objet est chiral s’il n’est pas superposable (non identique) à son image par un miroir plan.
Un objet non chiral est dit achiral.
—
Exemples :

Une coquille d’escargot n’est pas identique à son image par un miroir plan, elle est donc chirale !
Ce qui va nous intéresser évidemment c’est de savoir si une molécule est chirale ou non.
Voyons donc des exemple avec des molécules :
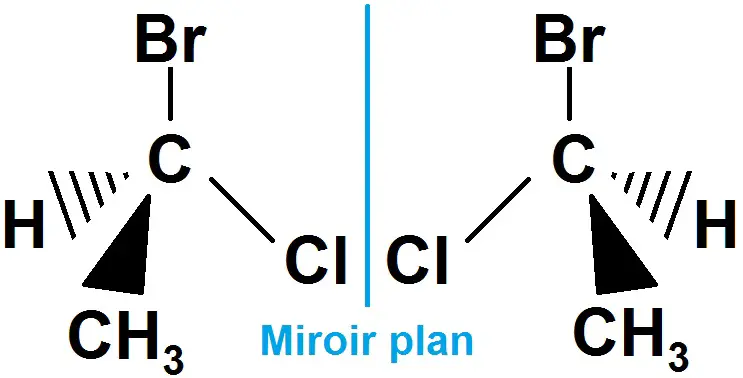
Les deux molécules ne sont pas identiques (même si on la retourne dans tous les sens) : c’est une molécule chirale.
En revanche :
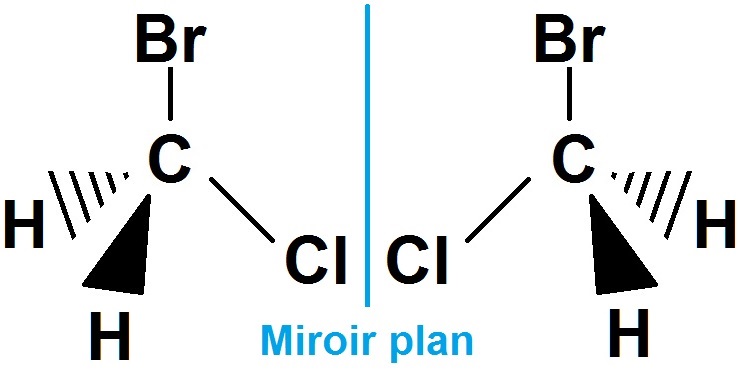
Les deux molécules sont identiques : c’est une molécule achirale (si on fait faire un demi-tour à la molécule de droite, on retrouvera celle de gauche).
Pour savoir si une molécule est chirale ou non, on fait donc son image par un miroir plan et on regarde si on trouve une molécule identique ou non.
Mais il existe un cas particulier très fréquent : le carbone asymétrique.
Comme on l’a rappelé ci-dessus, un atome de carbone fait 4 liaisons.
Si l’atome de carbone est relié à 4 atomes ou groupes d’atomes tous différents, on dit que c’est un carbone asymétrique.
On le note alors avec une étoile : C*.
Exemple :
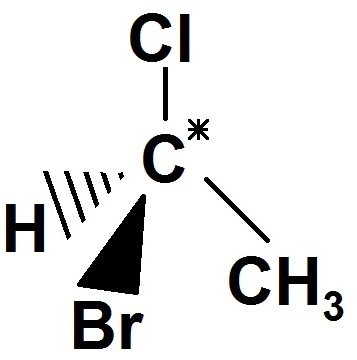
Le carbone est relié à CH3, Cl, Br et H, qui sont 4 groupes d’atomes différents, donc c’est un carbone asymétrique.
Autre exemple :
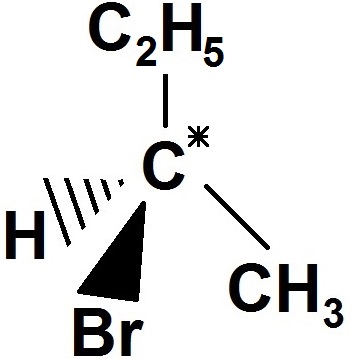
Le carbone est relié à CH3, C2H5, Br et H, qui sont 4 groupes d’atomes différents, donc c’est un carbone asymétrique.
A noter que ce carbone asymétrique est directement relié à 2 carbones (1 du CH3 et 1 du C2H5), mais comme le groupe d’atomes est différent cela marche quand même (CH3 est différent de C2H5).
Il y a alors une règle très importante à retenir :
—
Une molécule possédant un seul carbone asymétrique est toujours chirale.
—
Attention, la réciproque n’est pas vraie !
C’est-à-dire qu’une molécule chirale n’a pas nécessairement un seul carbone asymétrique, elle peut en avoir plusieurs comme elle peut ne pas en avoir !
Ainsi, si la molécule n’a aucun C* ou plus de deux, on ne peut pas utiliser la règle ci-dessus pour dire si elle est chirale ou non, il faut faire son image par un miroir plan pour le savoir.
Ainsi, si on prend la molécule suivante :

Développons-la pour voir quels carbones sont asymétriques :
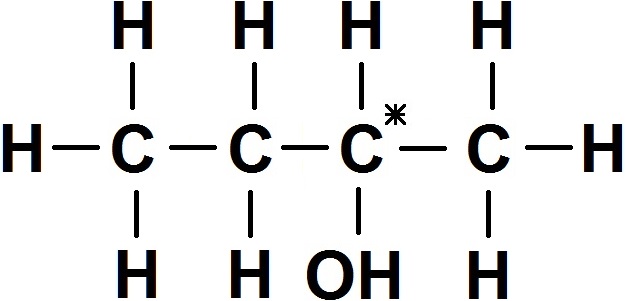
On voit que la molécule possède un seul carbone asymétrique (celui avec l’étoile), donc elle est chirale !
En effet, les autres carbones sont reliés à plusieurs H, donc ils ne sont pas asymétriques.
Passons enfin au cœur du chapitre : les stéréoisomères !
Donnons déjà une définition : des stéréoisomères sont des molécules ayant la même formule semi-développée, mais un agencement des atomes dans l’espace différent.
Ainsi la représentation de Lewis sera la même, il faut donc représenter la molécule avec Cram pour identifier les stéréoisomères.
Exemple : la molécule CHClBrCH3.
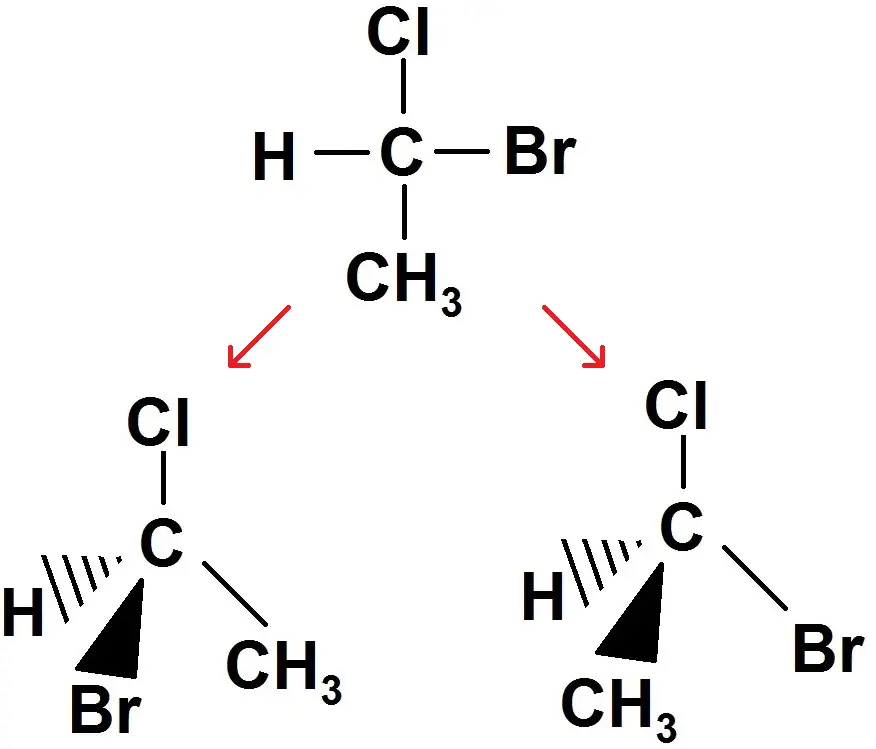
On voit que la représentation de Lewis est la même, mais avec Cram ou trouve deux stéréoisomères (il peut y en avoir d’autres).
Attention, une même molécule peut avoir des représentations de Cram différentes comme on l’a vu (suivant le point d’observation), donc il faut bien s’assurer que l’on a des agencements spatiaux différents. Si on a juste un point de vue différent, il ne s’agit pas de stéréoisomères.
Quand on a trouvé deux stéréoisomères, il peut y avoir deux cas :
– soit on passe de l’un à l’autre par une simple rotation : il s’agit alors de stéréoisomères de conformation ;
– soit il faut casser une liaison pour la remettre ailleurs : il s’agit alors de stéréoisomères de configuration.
Nous parlerons des stéréoisomères de conformation en fin de chapitre car ce sont ceux que l’on rencontre le moins souvent, car il y a moins de questions possibles (en tout cas au lycée).
Nous allons donc tout d’abord étudier les stéréoisomères de configuration.
Là encore il y a deux possibilités :
– soit les stéréoisomères sont images l’un de l’autre par un miroir plan : on parle d’énantiomères ;
– soit les stéréoisomères ne sont pas images l’un de l’autre par un miroir plan : on parle de diastéréoisomères.
Ces mots ont l’air compliqués à retenir mais avec l’entraînement tu verras que c’est assez simple !
Voyons un exemple simple :

Le Br est toujours en haut, le CH3 devant et le H derrière. En revanche, le Cl qui était à droite se retrouve à gauche : il faut donc « casser » la liaison, on ne peut pas faire une simple rotation, ce sont donc bien des stéréoisomères de configuration.
Les molécules sont bien images l’une de l’autre, ce sont donc des énantiomères ! 
Tu as peut-être remarqué que la molécule ci-dessus possède un seul carbone asymétrique : c’est donc une molécule chirale.
Mais on peut aller plus loin en disant qu’une telle molécule peut exister sous deux configurations différentes, qui sont énantiomères.
On a en effet la règle suivante :
—
Une molécule possédant un seul carbone asymétrique peut exister sous deux configurations différentes, qui sont énantiomères l’une de l’autre.
—
C’est un cas particulier que l’on rencontre souvent en exercices !
Pour généraliser ce cas particulier, on peut considérer 4 groupes d’atomes différents A, B, D et E (le C est le carbone asymétrique), on a alors :
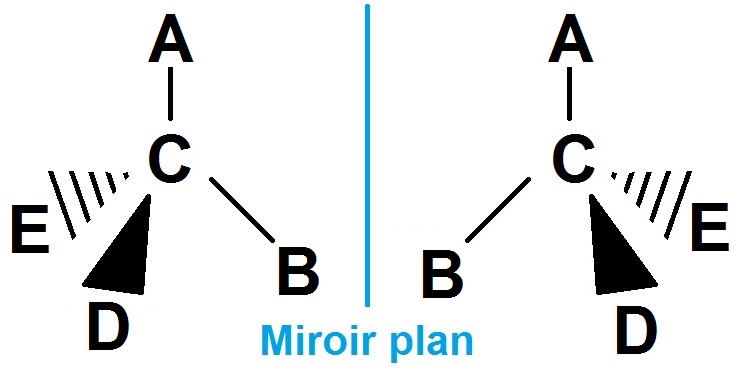
Une telle molécule n’a pas d’autre configuration, donc pas de diastéréoisomère.
Avant de passer au cas avec deux carbones asymétriques, rajoutons un peu de vocabulaire.
On considère une molécule possédant deux énantiomères (comme l’exemple ci-dessus).
Si dans un mélange il y a autant de l’un que de l’autre, on dit que le mélange est racémique.
—
Un mélange contenant deux énantiomères en proportion égale est appelé mélange racémique.
On dit que le mélange est équimolaire (autant de mols de l’un que de l’autre).
—
Un cas que l’on rencontrera souvent est celui avec 2 carbones asymétriques.
Ces 2 carbones sont reliés entre eux, et chacun est relié à trois autres groupes d’atomes différents, selon la représentation de Cram.
Ainsi dans le cas général :
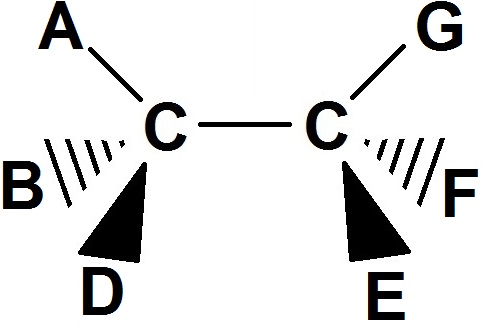
A, B et D sont trois groupes d’atomes différents, tout comme E, F et G, puisque les 2 carbones sont asymétriques.
Une telle molécule possède toujours 4 stéréoisomères de configuration que l’on peut séparer en 2 groupes de 2.
Les 2 du 1er groupe sont énantiomères, tout comme les 2 de l’autre groupe. Et chacun est énantiomère avec l’autre groupe.
On peut schématiser de la manière suivante :
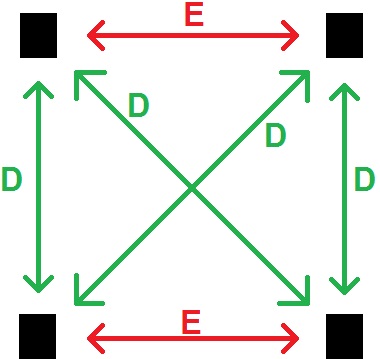
Les 4 rectangles noirs sont des stéréoisomères, E signifie une relation d’énantiomérie, et D une relation de diastéréoisomérie.
Comment trouver la représentation de chacune des molécules ?
C’est plutôt simple si tu appliques le principe décrit ci-dessous.
Supposons que l’on cherche les stéréoisomères de configuration de la molécule suivante :
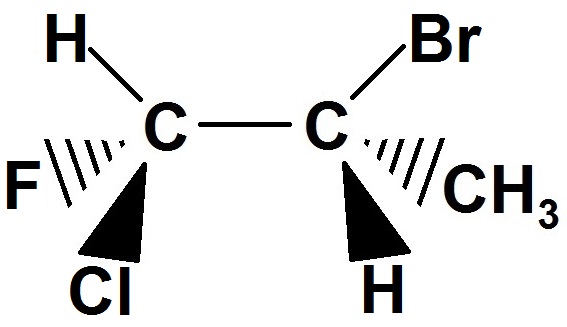
1) tu mets cette molécule de référence en haut à gauche du schéma précédent.
2) Pour trouver l’énantiomère, tu inverses tout ce qui est devant et derrière (triangle plein et en pointillés).
Ainsi, ce qui était au bout d’un triangle plein se retrouve au bout d’un triangle en pointillés et inversement. Tu as donc 4 groupes d’atomes à changer (que l’on a mis en couleur ci-dessous). Tout le reste ne change pas :
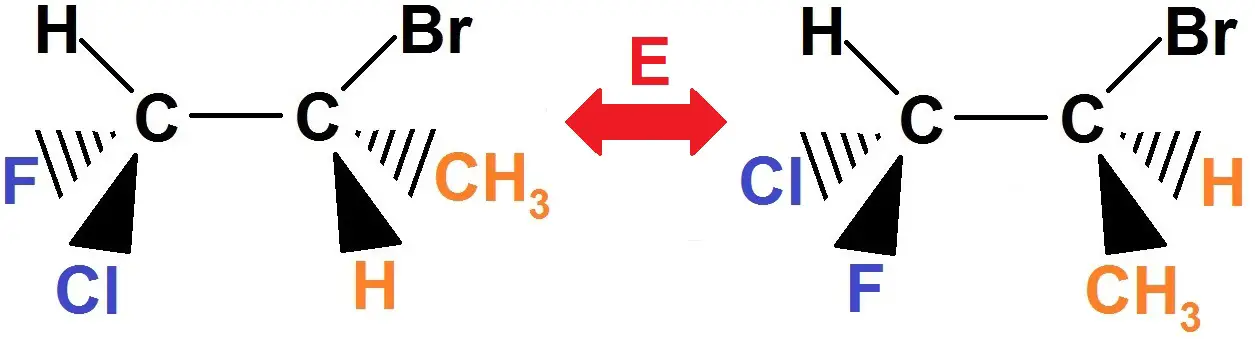
En fait, cela revient à faire l’image par un miroir qui se situe dans le plan de la feuille : comme c’est l’image par un miroir plan, il s’agit bien d’énantiomères.
3) Pour trouver le 1er diastéréoisomère, on fait la même chose mais en ne changeant qu’un seul couple devant-derrière !!.
Pour trouver le 2ème diastéréoisomère, il suffira d’inverser uniquement l’autre couple.
Et comme précédemment le reste ne change pas :
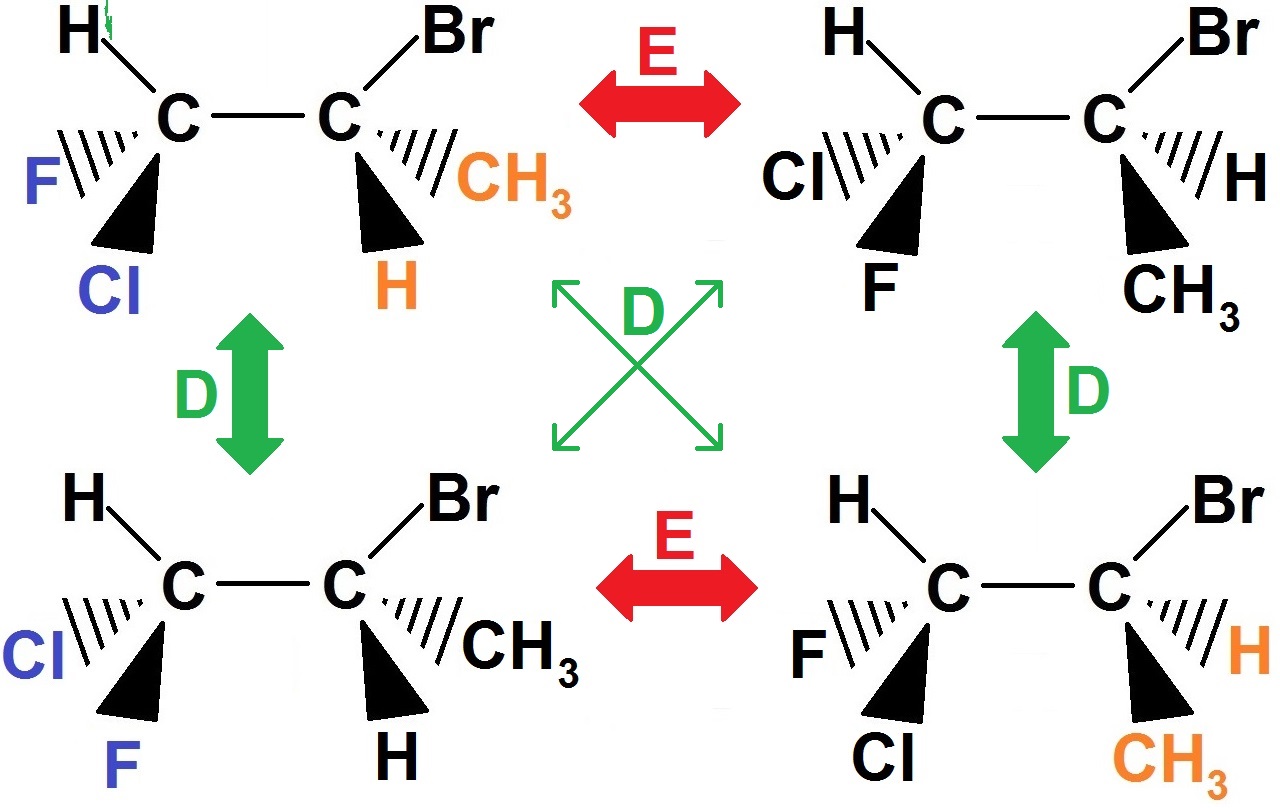
Nous avons mis en couleur uniquement ce qui change par rapport à la molécule en haut à gauche : pour les deux diastéréoisomères, il n’y a à chaque fois qu’un seul couple qui change (le bleu ou le orange).
On peut remarquer que ces deux nouvelles molécules sont bien énantiomères car les deux sont identiques sont les couples devant-derrière qui ont été inversés : exactement le même principe que les deux molécules au-dessus !!
Pour résumer :
—
Si on inverse les 2 couples devant-derrière, on obtient un énantiomère.
Si on inverse 1 seul couple devant-derrière, on obtient un diastéréoisomère.
—
La représentation de Cram ci-dessus est souvent utilisée mais on trouve également la représentation de Fischer, dans laquelle on regarder la molécule par « au-dessus ».
Ce qui est devant dans Cram se retrouve à gauche dans Fischer, et ce qui est derrière dans Cram se retrouve à droite dans Fischer.
Le reste se retrouve sur un axe vertical (notamment la liaison C – C).
Exemple :
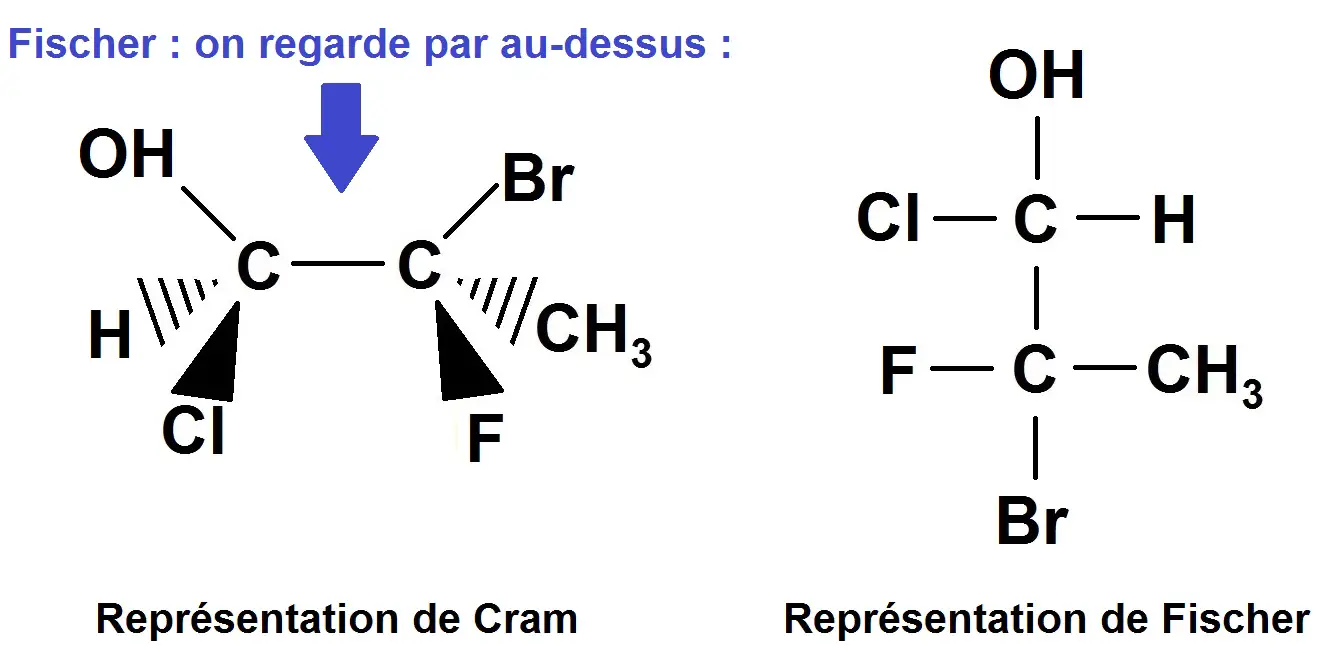
Comme tu le vois, le F et le Cl qui étaient devant dans Cram se retrouvent à gauche dans Fischer, le H et le CH3 qui étaient derrière se retrouvent à droite.
Le Br et le OH qui étaient dans le plan se retrouvent sur l’axe vertical.
Pour trouver les différents énantiomères et diastéréoisomères même principe : on inverse ce qui devant avec ce qui derrière dans Cram, c’est-à-dire ce qui est à gauche avec ce qui est à droite dans Fischer :
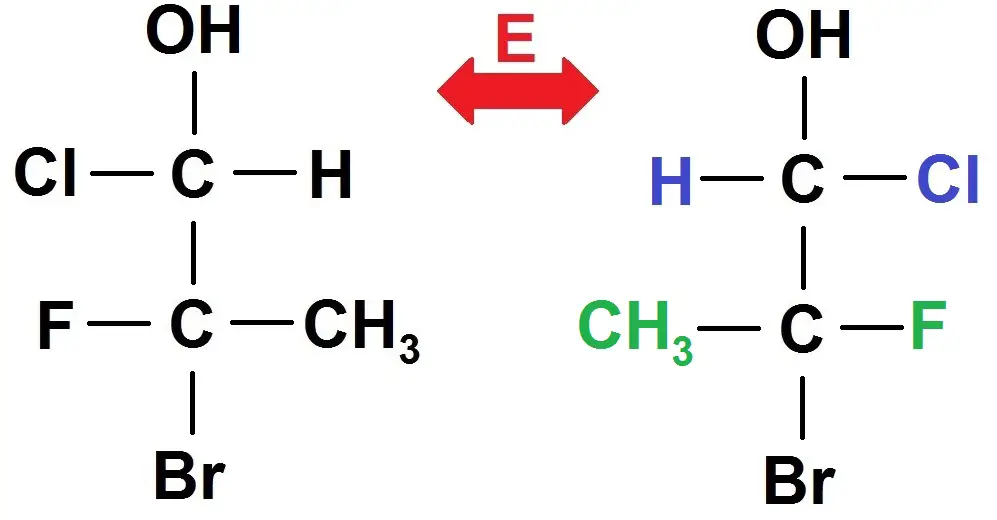
On retrouve évidemment le même principe : si on inverse les 2 couples gauche-droite, on obtient un énantiomère, et si on inverse 1 seul couple couple gauche-droite, on obtient un diastéréoisomère.
Tu auras peut-être remarqué que pour les énantiomères, ils sont symétriques par rapport à un plan imaginaire (en pointillés ci-dessous), ce qui confirme bien qu’ils sont énantiomères :
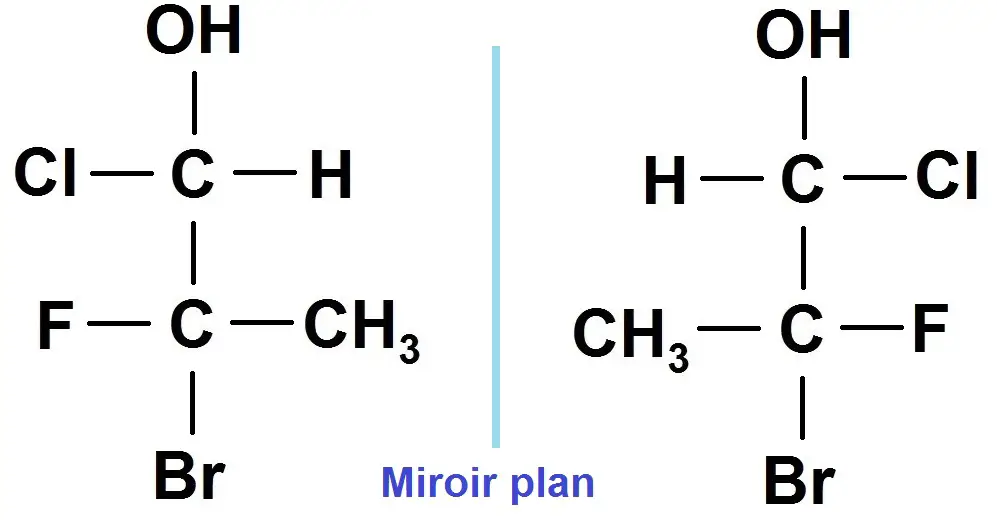
Nous reviendrons sur tout cela dans les exercices en vidéo !
La diastéréoisomères Z / E est uniquement valable pour les molécules présentant une double liaison C = C. Cette double liaison empêche toute rotation autour de cette liaison.
Il faut par ailleurs que ces 2 atomes de carbone soient liés à deux groupes d’atomes différents.
Exemples :
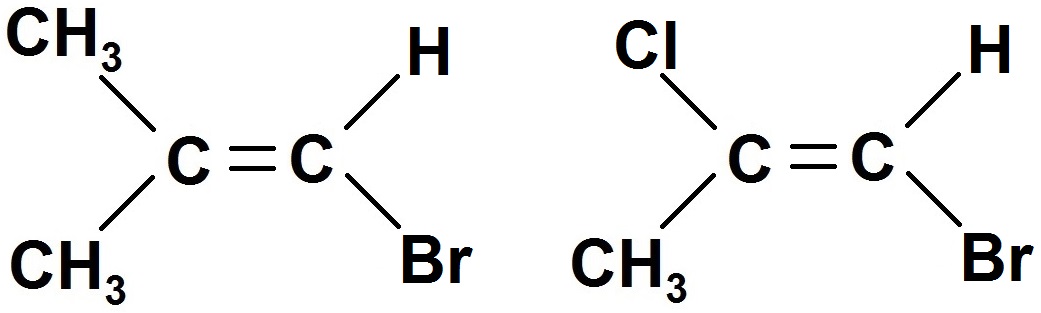
Dans la molécule de gauche, un carbone est lié à 2 groupes d’atomes identiques (CH3), donc il n’y a pas d’isomérie Z / E.
En revanche, dans la 2ème molécule, chaque C est relié à des groupes d’atomes différents, donc il y a une isomérie Z / E.
Si les conditions sont réunies, on a alors 2 configurations différentes : Z et E.
—
Z signifie Zusammen, qui veut dire « ensemble » en Allemand.
E signifie Entgegen, qui veut dire « opposé » en Allemand.
—
On pourrait penser que E veut dire Ensemble, mais non, c’est le contraire justement !! 
Pour retenir facilement, dis-toi que E ne signifie PAS Ensemble, car c’est de l’Allemand donc ce n’est pas pareil qu’en Français…
Mais qu’est-ce qui est ensemble ou opposé ??
Ce sont les groupes d’atomes prioritaires reliés aux deux 2 carbones.
Chaque carbone est en effet relié à 2 groupes d’atomes différents : parmi ces 2 groupes, un des deux est dit prioritaire.
Pour déterminer lequel, il faut appliquer ce que l’on appelle règles de Cahn, Ingold et Prelog.
D’après ces règles :
– si un atome a un numéro atomique plus élevé, il est prioritaire.
– si les atomes reliés directement au carbone (qu’on appelle atomes de premier rang) sont les mêmes, on passe aux atomes qui leurs sont liés (on les appelle atomes de second rang) et ainsi de suite jusqu’à ce qu’on arrive à une différence et donc trouver une priorité.
– si on arrive à une bifurcation sans pouvoir conclure, on choisit le chemin correspondant à l’atome prioritaire des deux séries identiques et on regarde le chemin prioritaire. On ne développera pas cette règle car elle se rencontre rarement au lycée.
Exemple :
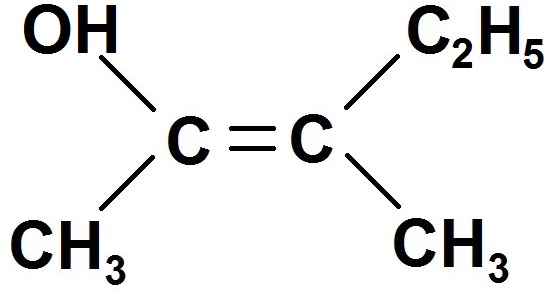
Pour savoir qui est relié à qui, il est conseillé d’écrire la formule développée et non la semi-développée :
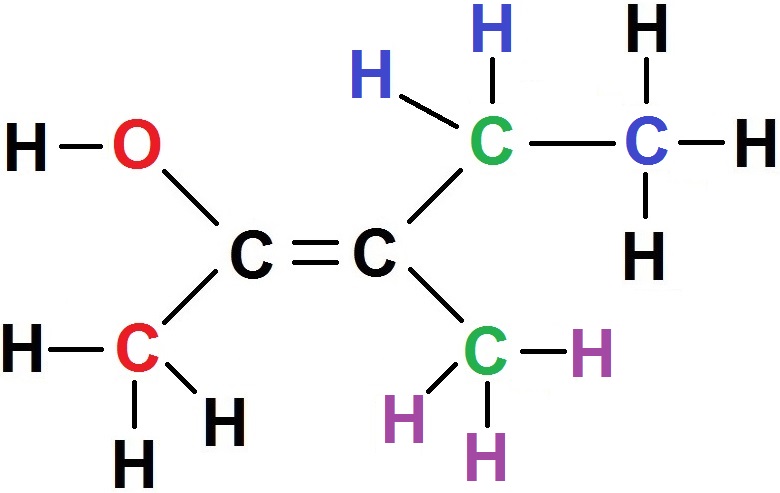
Pour le carbone de gauche, il est relié directement à C et à O (en rouge).
Or Z(O) > Z(C) d’après le tableau périodique, donc OH est prioritaire devant CH3.
On écrit OH > CH3.
Pour le carbone de droite, il est relié directement à C et à C (en vert).
On ne peut pas conclure car ce sont les mêmes atomes ! On regarde alors les atomes reliés à ces 2 carbones en vert.
Celui du dessus est relié à H, H et C (en bleu), celui du bas à H, H et H (en violet).
Z(C) > Z(H) donc C2H5 est prioritaire devant CH3.
On écrit C2H5 > CH3.
Ainsi les 2 groupes prioritaires sont OH et C2H5.
Il ne reste plus qu’à regarder s’ils sont du même côté (ensemble) ou pas.
Pour ce faire, on peut tracer en pointillés une ligne traversant la double liaison de la manière suivante :
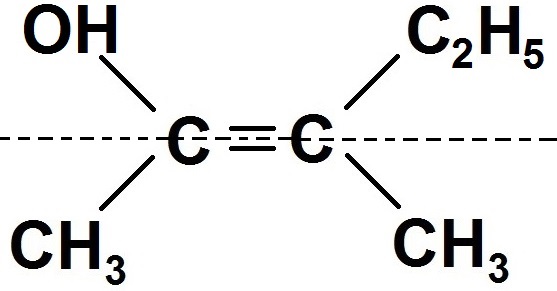
Cette ligne imaginaire (on n’est pas obligé de la tracer) sépare la molécule en 2 zones.
On voit clairement que OH et C2H5 sont dans la même zone, donc ensemble, c’est donc la configuration Z !
Pour avoir la configuration E, il suffit d’inverser les atomes de gauche (ou ceux de droite) :
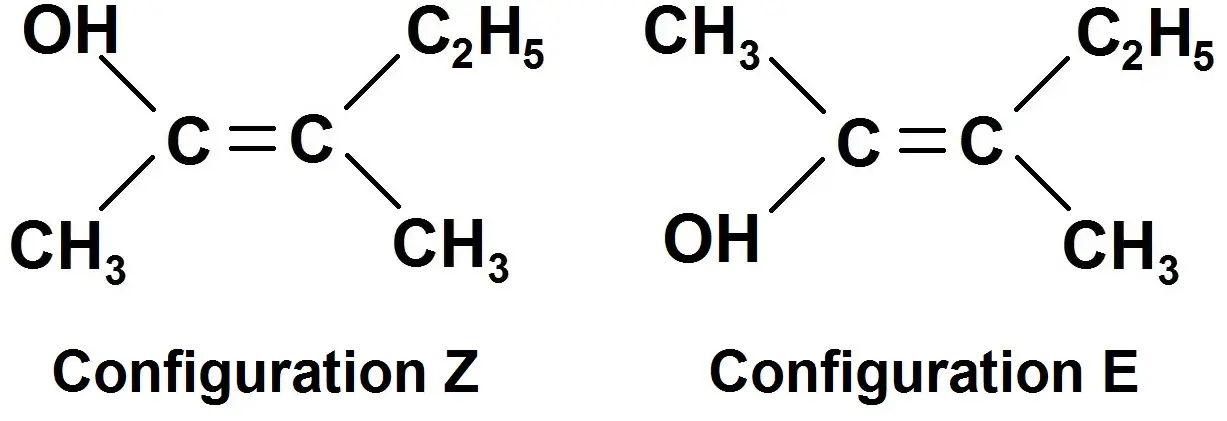
On voit maintenant que OH et C2H5 ne sont pas dans la même zone, c’est donc la configuration E !
Nous verrons d’autres exemple dans les exercices 
Les stéréoisomères de conformation sont des molécules qui différent par une rotation autour de liaisons simples, il ne faut pas les confondre avec les stéréoisomères de configuration qui ne peuvent s’obtenir par simple rotation.
La plupart du temps, nous aurons une liaison entre deux carbones (C – C), et l’on fera tourner cette liaison pour avoir des conformations différentes.
En 3D, on obtient :
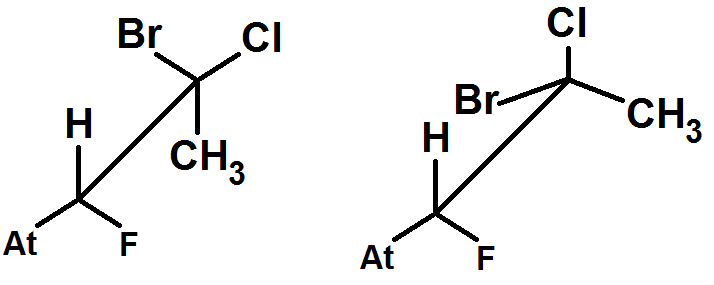
Dans la molécule de droite, on a uniquement fait tourner la liaison C – C.
Prenons un observateur qui regarde la liaison C – C face à lui, il verra alors devant lui les 3 groupes d’atomes reliés au 1er C, et derrière les 3 groupes d’atomes reliés au 2ème C.
On utilise alors la projection de Newman pour représenter cela :
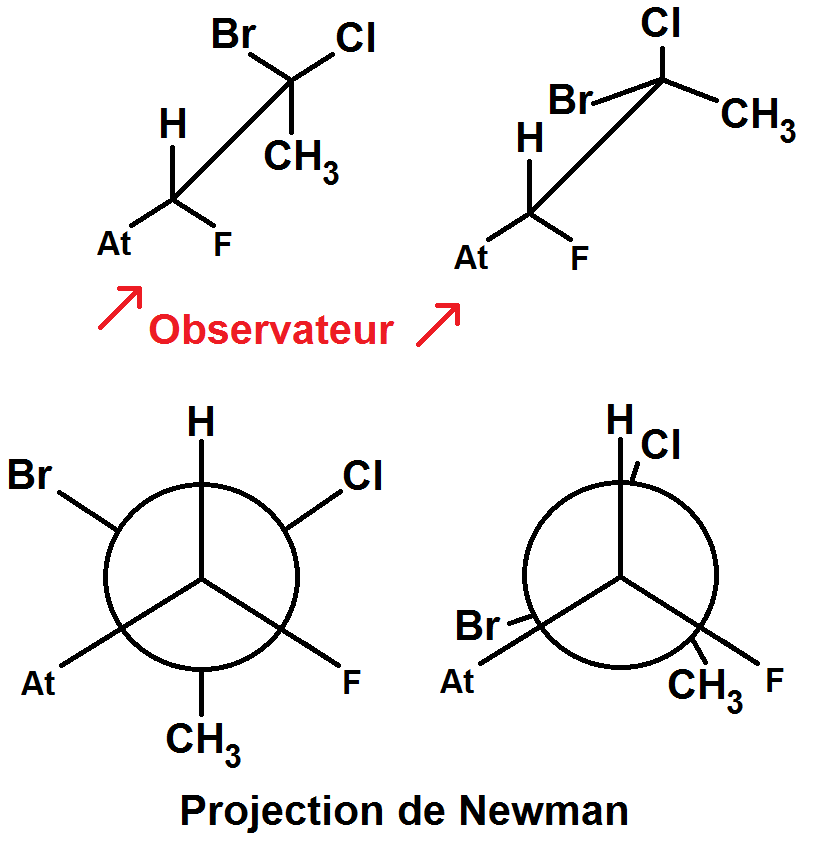
A droite, les atomes devant et derrière sont normalement alignés mais on les décale légèrement pour bien comprendre ce qui se passe.
Les deux conformations ci-dessus sont particulières car dans celle de gauche, les groupes d’atomes devant et derrière sont alignés, et dans celle de droite, ceux de derrière sont en « opposition de phase » par rapport à ceux de devant : ils sont décalés d’un angle de 60°.
Ces deux conformations ont des noms particuliers : éclipsée et décalée.
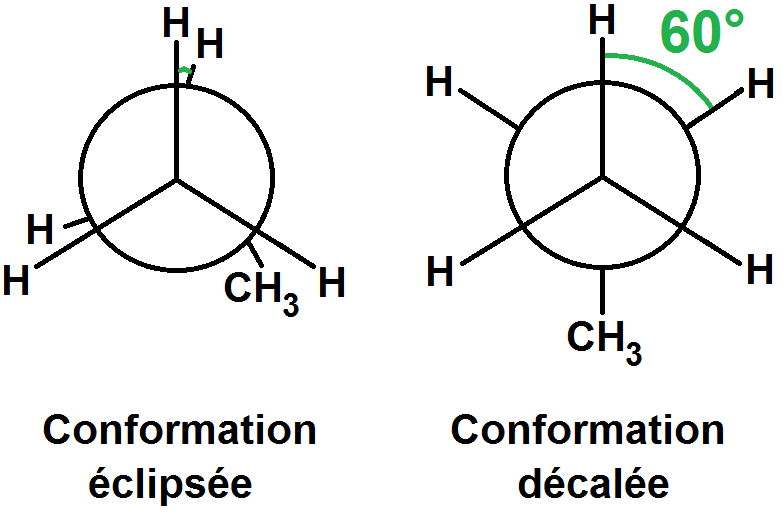
Pour se souvenir laquelle est la décalée et l’autre l’éclipsée, c’est très simple !
Éclipsée vient évidemment du mot éclipse, qui a lieu quand le soleil est cachée par une planète parce qu’elle est alignée.
Donc aligné = éclipsé.
Et décalé veut justement dire que ce n’est pas aligné mais… décalé ! 
Cet angle, qui dans l’exemple ci-dessus vaut 60° pour une conformation décalée et 0° pour une conformation éclipsée, est important car à partir de cet angle on va pouvoir déterminer l’énergie potentielle de la molécule.
En effet, chaque molécule possède une énergie potentielle due à la répulsion entre les groupes d’atomes : plus ceux-ci sont proches, puis ils se repoussent, et donc plus l’énergie potentielle est élevée.
De plus, quand la molécule possède des groupes d’atomes différents, l’énergie potentielle est plus élevée quand les plus lourds sont les plus proches, et au contraire plus faible quand ils sont plus éloignés.
Le but est de tracer l’énergie potentielle de la molécule en fonction de l’angle que l’on appelle α.
Voyons un exemple simple :
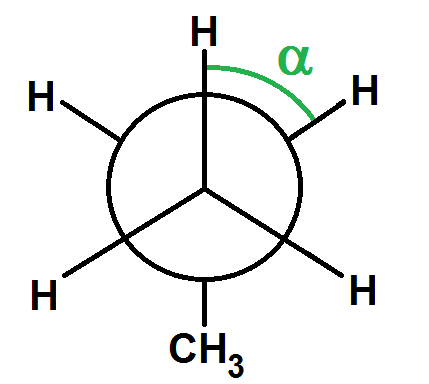
Ici c’est simple car un des carbones est relié à 3 atomes identiques (H).
Pour α = 0° l’énergie potentielle est maximale car les atomes sont les plus proches.
Pour α = 60°, l’énergie potentielle est minimale car les atomes sont les plus éloignés :
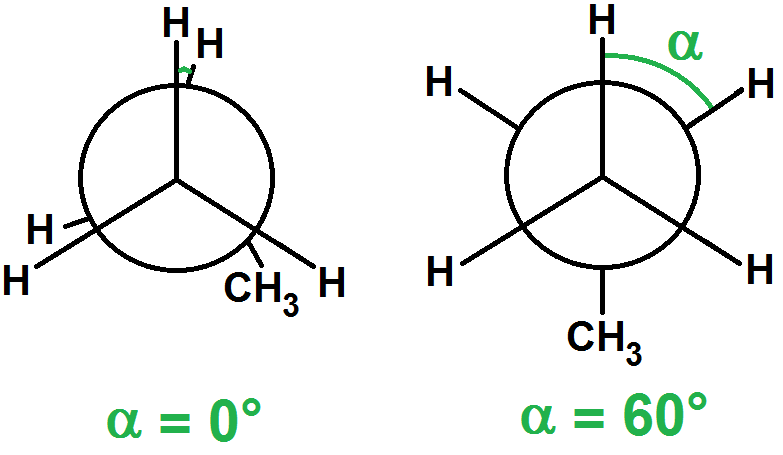
Pour α = 120°, on retrouve la même situation que pour 0°, et de même pour α = 240° :
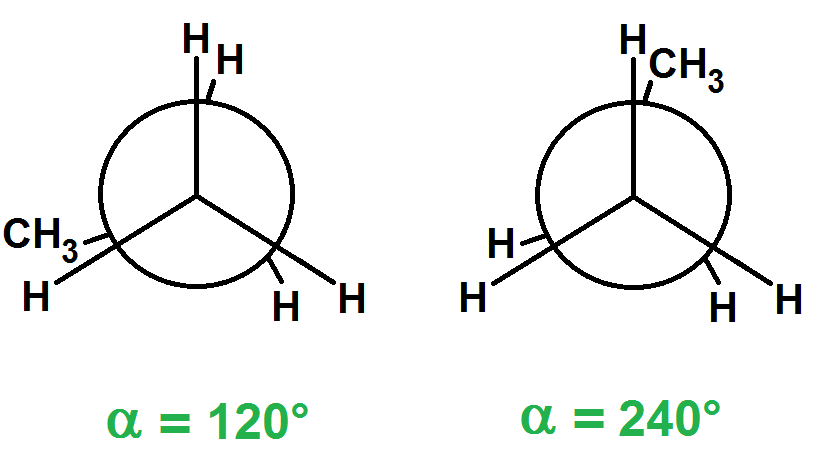
De la même manière, les situations pour α = 180° et 300° sont identiques à 60° (cela est dû au fait qu’un des C est relié à 3 H).
On obtient alors le graphique suivant :
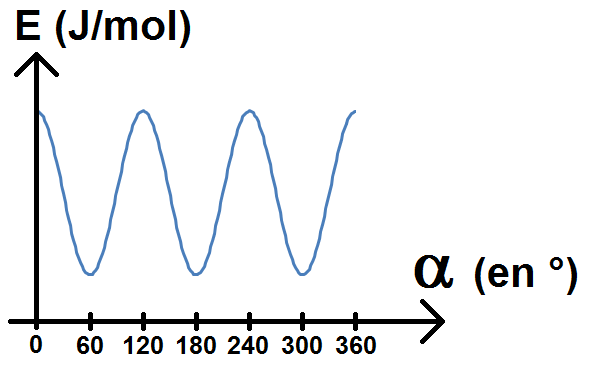
Pour accéder aux exercices sur ce chapitre, clique ici !
Sommaire des coursHaut de la page


