Sommaire
Introduction
Principe général
Conductivité et résistance thermiques
Superposition de matériaux
Exercices
Nous parlerons dans ce chapitre de transferts thermiques à travers une (ou plusieurs) parois.
Le mot thermique a la même racine que le mot thermomètre : il va donc être question de température. Et plus particulièrement des températures de part et d’autre d’une paroi. Si les deux températures sont différentes, il y aura un transfert d’énergie : c’est un transfert thermique !
En effet, en hiver par exemple, il fait plus chaud à l’intérieur de la maison qu’à l’extérieur : il y a donc du « chaud » (de l’énergie) qui va traverser les murs et les fenêtres de la maison.
Ce transfert thermique se fait toujours de la température la plus chaude vers la température la plus froide.
Il faut penser en effet que l’énergie, c’est du chaud !
Comme le chaud a tendance à réchauffer le froid, l’énergie va du chaud vers le froid.
Pour modéliser tout cela, on va prendre une paroi d’épaisseur e, avec deux températures T1 et T2 de part et d’autre de la paroi.
Le transfert d’énergie est matérialisé par un flux noté Φ (prononcer phi) représenté par une flèche, qui traverse la paroi de la température la plus chaude vers la température la plus froide :
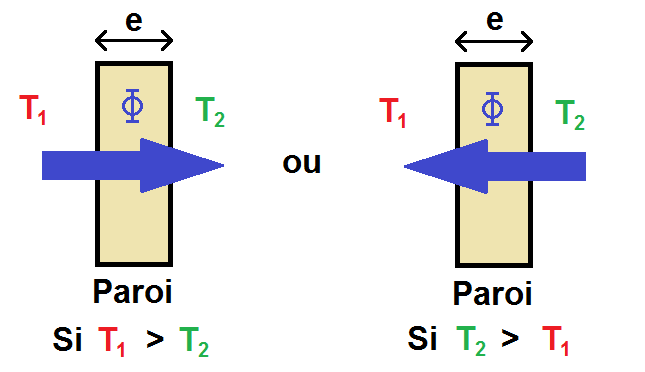
En réalité, il ne faut pas prendre en compte uniquement l’épaisseur de la paroi mais aussi sa surface.
Il faut donc faire un schéma en 3D (nous prendrons uniquement le cas T1 > T2) :
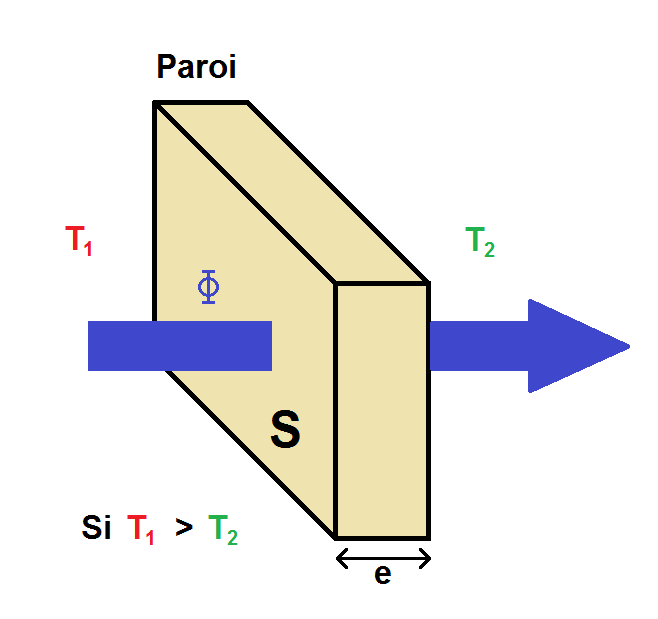
Dans ce graphique, on a :
Φ le flux en W (Watt) ;
e l’épaisseur de la paroi traversée par le flux en m ;
S la surface de la paroi traversée par le flux en m2 ;
T1 et T2 les températures de part et d’autre de la paroi EN KELVINS !!!.
En effet, en physique-chimie, l’unité de base des températures n’est pas le degré Celsius que l’on utilise habituellement mais le Kelvin noté K.
Nous y reviendrons un peu plus bas.
Toutes ces données sont regroupées dans deux formules que nous allons détailler.
—
Remarque : le flux se note Φ (phi majuscule) mais il peut parfois être noté φ (phi minuscule).
Cela revient strictement au même, tout dépend de l’énoncé, donc ne sois pas étonné si tu vois un jour le flux noté φ.
—
En plus de Φ, e, S, T1 et T2, nous allons rajouter deux données.
La première est la conductivité thermique, notée λ (à ne pas confondre avec la longueur d’onde vue dans le chapitre sur les ondes !!).
λ est caractéristique du matériau de la paroi, quel que soit les dimensions de la paroi.
Comme son nom l’indique, λ définit la conductivité du matériau, c’est-à-dire sa capacité à conduire l’énergie, à transférer l’énergie.
Ainsi, plus λ est grand, plus le matériau laisse passer facilement la chaleur.
A l’inverse, plus λ est petit, plus le matériau est isolant.
Pour isoler une maison, on utilise donc des matériaux avec un faible λ comme la laine de verre par exemple.
Pour finir, λ est en W.m-1.K-1
La deuxième donnée est la résistance thermique, notée Rth.
Cette résistance thermique (qui s’apparente à la résistance en électricité) caractérise toute la paroi. Sa valeur va dépendre du matériau de la paroi, mais aussi de son épaisseur et de sa surface, contrairement à λ qui ne dépend que du matériau.
De plus, à l’inverse de λ, Rth mesure la capacité de la paroi à isoler : donc plus Rth est grand, plus la paroi est isolante, et plus Rth est petit plus la paroi laisse passer l’énergie : c’est le raisonnement inverse de la conductivité λ !!.
Pour finir, Rth est en K.W-1.
Nous avons désormais toutes les données qui vont apparaître dans les formules.
Commençons par la première formule :
\(\displaystyle R_{th} = \frac{e}{\lambda S} \)
Cette formule est tout à fait logique avec ce que l’on a dit précédemment !
En effet, on voit que Rth est inversement proportionnel à λ (car au dénominateur) : normal car on a vu que plus λ est petit plus la matériau est isolant. Rth sera alors plus grand et la paroi sera donc plus isolante : tout est ok !
Rth est également inversement proportionnel à S : normal car plus la surface sera petite moins l’énergie pourra passer et plus la paroi sera donc isolante (Rth sera plus grand).
Enfin, Rth est proportionnel à e : normal car plus la paroi est épaisse, plus la paroi sera isolante et donc Rth grand.
Le fait de retenir l’aspect logique de la formule t’aidera à la retrouver si jamais tu l’oublies ou que tu as un doute 
Passons à la deuxième formule :
\(\displaystyle R_{th} = \frac{|T_2 – T_1|}{\phi} \)
Encore une fois cette formule est tout à fait logique !
Plus Φ est grand plus il y a d’énergie qui passe à travers la paroi et donc la paroi est moins isolante : Rth sera plus petit. Il est donc normal que Φ et Rth soient inversement proportionnels.
A l’inverse, |T2 – T1| représente la différence de température entre les deux côtés de la paroi.
Plus Rth est grand, plus la paroi est isolante et donc chaque côté de la paroi gardera sa température : la différence de température sera donc plus importante. Donc Rth est bien proportionnel à la différence de température.
Remarque : |T2 – T1| étant en Kelvins et Φ en W, cela montre bien que Rth est en K.W-1.
—
ATTENTION : tu as sans doute remarqué la valeur absolue à |T2 – T1|.
Mais pourquoi donc ??
Tout simplement parce que Rth et Φ sont positifs, il faut donc une différence de température positive.
Si T2 > T1, T2 – T1 sera positif.
Mais si T1 > T2, T2 – T1 sera négatif !
Pour faire le cas général, on prend donc la valeur absolue comme ça on n’a pas à se soucier de savoir quelle température est la plus grande.
On peut évidemment prendre |T1 – T2| à la place de |T2 – T1|, ça ne change rien puisque l’on est en valeur absolue !
—
Il y a donc deux formules pour Rth :
\(\textstyle R_{th} = \frac{e}{\lambda S} \)
\(\textstyle R_{th} = \frac{|T_2 – T_1|}{\phi} \)
On peut donc regrouper les deux formules en une seule :
\(\textstyle \frac{e}{\lambda S} = \frac{|T_2 – T_1|}{\phi} \)
A partir de là, on peut isoler une des donnée et la calculer à partir de la valeur des autres variables données dans l’énoncé.
Par exemple si on cherche e :
\(\textstyle e = \frac{\lambda S \times|T_2 – T_1|}{\phi} \)
Si on cherche λ :
\(\textstyle \lambda = \frac{\phi \times e }{S \times|T_2 – T_1|} \)
Cette formule montre bien au passage pourquoi λ est en W.m-1.K-1 (amuse toi à faire la démonstration  ).
).
Evidemment il faut mettre les différentes valeurs dans la bonne unité.
—
Remarque : on a vu plus haut que les températures devaient être en °K et non en °C.
Pour passer des Celsius aux Kelvins, il faut faire + 273,5.
Par exemple 20 °C = 20 + 273,5 = 293,5 °K.
Autre exemple : 35 °C = 35 + 273,5 = 308,5 °K.
Or ici on fait une DIFFÉRENCE de température… qui est la même en Celsius et en Kelvins !
En effet, prenons T1 = 12 °C et T2 = 35 °C, soit T1 = 285,5 °K et T2 = 308,5 °C
En Celsius : |T2 – T1| = |35 – 12| = 23 °C.
En Kelvins : |T2 – T1| = |308,5 – 285,5| = 23 °K.
La différence de température est la même en °C et en °K !
On peut donc EXCEPTIONNELLEMENT ne pas convertir les températures en °K quand on fait une différence de température.
—
Nous avons vu jusqu’à présent le cas où les deux milieux de température T1 et T2 sont séparés par une paroi constituée d’un seul matériau. Mais ce n’est pas toujours le cas !
En effet, un double vitrage est constitué de 2 épaisseurs de verre séparés par une couche d’air.
Autre exemple : le toit d’une maison, constitué d’une couche de tuile, d’une couche de laine de verre et d’une couche de bois.
On modélise alors la situation de la manière suivante :
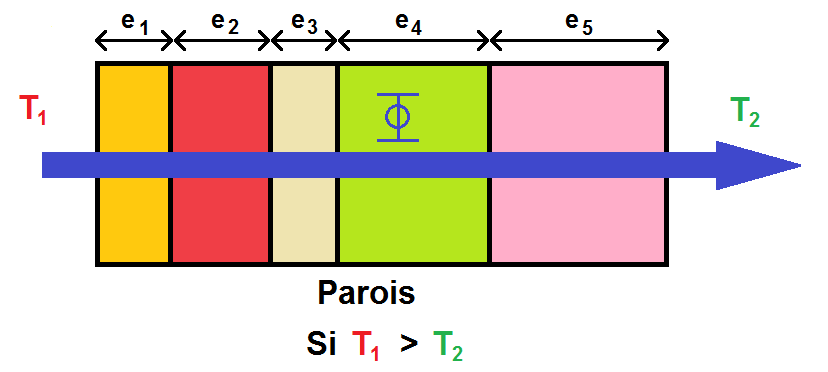
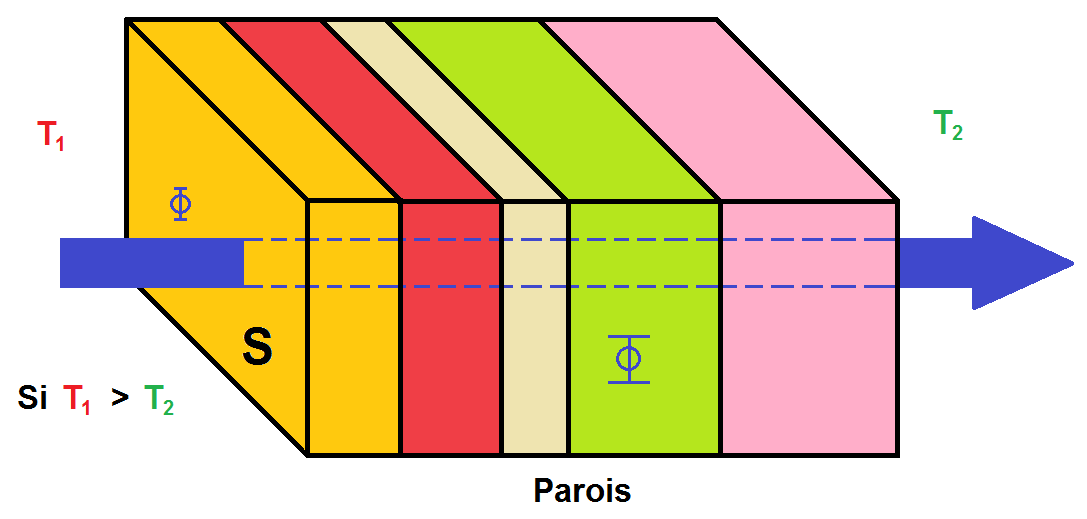
Comment sont modifiés les calculs précédents dans ces cas-là ?
C’est en réalité assez simple : chaque paroi a une épaisseur, notée e1, e2, e3…, mais une également un λ différent car les matériaux sont différents. Il sont notés λ1, λ2, λ3…
En revanche la surface est la même, elle est notée S.
Chaque paroi a donc une résistance thermique : Rth1, Rth2, Rth3…
\(\textstyle R_{th1} = \frac{e_1}{\lambda_1 S} \)
\(\textstyle R_{th2} = \frac{e_2}{\lambda_2 S} \)
etc…
—
Le principe est le suivant : la résistance thermique équivalente est égale à la somme des résistances thermiques des différentes parois
—
\(\displaystyle R_{th} = R_{th1} + R_{th2} + R_{th3} + R_{th4} + R_{th5} \)
Cette formule est évidemment vraie si on a 5 parois, si on en a plus ou moins on adapte la formule^^
—
Remarque : cette formule ressemble à la formule d’addition des résistances en série, qui s’écrit
R = R1 + R2 + etc…
Cela est logique car on a vu plus haut que la résistance thermique jouait le même rôle qu’une résistance électrique, et le fait de mettre des parois côte à côte revient à les mettre « en série », comme en électricité.
—
L’idée est donc de calculer les Rth de chaque paroi et de les additionner.
—
ATTENTION !! On n’additionne pas les λ !!!
En effet, les conductivités λ sont caractéristiques d’un matériau, et ce n’est pas parce que l’on met deux matériaux côte à côte que l’ensemble a une conductivité équivalente à la somme des deux, cela n’a aucune logique physique…
—
Par ailleurs, d’après le schéma, il n’y a qu’un seul flux qui traverse l’ensemble des parois, et non pas un flux pour chaque paroi.
On a donc toujours la formule
\(\textstyle R_{th} = \frac{|T_2 – T_1|}{\phi} \)
D’où :
\(\textstyle R_{th1} + R_{th2} + R_{th3} + R_{th4} + R_{th5} = \frac{|T_2 – T_1|}{\phi} \)
A partir de là on peut imaginer plein de calculs, tout dépendra de l’énoncé (nous verrons cela dans les exercices).
—
Remarque : les températures T1 et T2 sont là encore les températures de part et d’autre de la paroi.
Tu as remarqué qu’on ne prend pas en compte les températures entre chaque paroi…
—
Maintenant que tu sais tout passons aux exercices 
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !



T1 et T2 peuve être en celsus cela ne change rien si on cherche un differentiel de température ; )
bonjour j’aimerais savoir s’il y a une différence entre agitation thermique et transfert thermique
Oui le transfert thermique correspond à un échange d’énergie entre 2 systèmes. L’agitation thermique correspond au mouvement des molécules au niveau microscopique.
super!! cours limpide!!!
votre cours est super bien detaillee . j’aimerai bien voire des exercice poue bien developper mes capasite