Sommaire
Introduction
Notion de pression
Fluide homogène incompressible
Loi de la statique des fluides
Théorème de Pascal
Exercices
Ce chapitre est assez court mais n’en reste pas moins important car il s’agit d’un chapitre préliminaire à celui sur la mécanique des fluides, qui est plus complexe.
Comme son nom l’indique, la statique des fluides concerne des fluides qui ne bougent pas, alors que la mécanique des fluides concerne l’étude de fluides en écoulement. Dans ce qui suit, il n’y aura donc pas de notion de temps puisque tout est statique (à l’équilibre).
La variable qui va nous intéresser dans ce chapitre est la pression dans le fluide.
La pression correspond à une force surfacique qui s’exerce sur une surface sous l’action d’un fluide (liquide ou gaz).
La pression étant une force surfacique, elle s’exprime en N.m-2, mais elle s’exprime aussi en Pascal (noté Pa).
Il arrive que la pression soit aussi exprimée en bars pour plus de facilité, mais dans les formules il faudra absolument la convertir en Pa pour les calculs. On a l’égalité :
\(\displaystyle 1 \, bar = 10^5 \, Pa \)
Un fluide (de l’eau, de l’huile ou du dioxygène par exemple) est caractérisé par sa masse volumique notée ρ.
Cette masse volumique peut ne pas être la même partout dans le fluide, et dépendra a priori de la pression P et de la température T.
La plupart du temps ce ne sera pas le cas car on considérera des fluides homogènes et incompressibles pour simplifier les calculs.
On a en effet les définitions suivantes :
—
Un fluide est incompressible si ρ est indépendant de P.
Un fluide est homogène si ρ ne dépend pas du point de l’espace considéré. Si la température est la même partout, ρ ne dépendra pas de T.
—
Ainsi :
—
Pour un fluide incompressible et homogène, ρ est constante.
—
Cela va être important pour la suite, notamment quand on va intégrer des formules.
Le plus important dans le chapitre est la loi de la statique des fluides, aussi appelée relation fondamentale de la statique des fluides ou loi fondamentale de la statique des fluides. Elle est donc parfois abrégée RFS ou LFS.
Cette formule permet de trouver la pression en un point du fluide.
Elle s’écrit :
\(\displaystyle \overrightarrow{grad}(P) = \rho \vec{g} \)
Le gradient est l’opérateur vu dans le chapitre sur les opérateurs.
Le vecteur g étant vertical vers le bas, on a donc :
\(\textstyle \left(\begin{array}{c} \frac{\partial P}{\partial x} \\ \frac{\partial P}{\partial y} \\ \frac{\partial P}{\partial z} \end{array}\right) = \left(\begin{array} 0 \\ 0 \\ – \rho g \end{array}\right) \)
On en déduit que P ne dépend que de z, et que l’on a :
\(\displaystyle \frac{dP}{dz} = -\rho g \)
Le signe – vient du fait que g est dirigé vers le bas, alors que l’axe vertical est dirigé vers le haut.
—
Attention ! Si on prend un axe vertical dirigé vers le bas, il ne faut pas mettre de signe – dans la formule.
Toutes les formules ci-dessous devront alors être adaptées en conséquence.
—
Si on considère un fluide homogène incompressible, ρ est constant, et l’intégration de la formule précédente donne :
\(\textstyle P(z) = -\rho gz + constante \)
\(\textstyle P(z) + \rho gz = constante \)
Si on prend deux points A et B, on peut donc écrire :
\(\textstyle P(z_A)+B \rho gz_A = P(z_B) + \rho gz_B \)
\(\textstyle P(z_A) – P(z_B) = \rho gz_B – \rho gz_A \)
\(\textstyle (P(z_A) – P(z_B)) = -\rho g(z_A – z_B) \)
Autrement dit :
\(\displaystyle \Delta P = -\rho g \Delta z \)
Il s’agit de la loi fondamentale de la statique (LFS) simplifiée, mais tu pourras l’appliquer directement dans les exercices en disant « d’après la loi fondamentale de la statique : … », sans passer par le gradient.
Comme dit précédemment, la formule est valable pour un axe vertical ascendant, si on prend un axe descendant il ne faut pas mettre le signe -.
Cette formule sera très souvent utilisée dans les exercices (nous le verrons dans les exercices en vidéo).
Pour Δ P et Δ z, on prend deux points quelconques du fluide (attention, il faut que ce soit deux points du même fluide).
Remarque importante : on a vu que P(z) = ρ g z + constante, donc P ne dépend que de z.
Ainsi, deux points à la même hauteur dans un fluide auront la même pression.
Voyons un exemple :
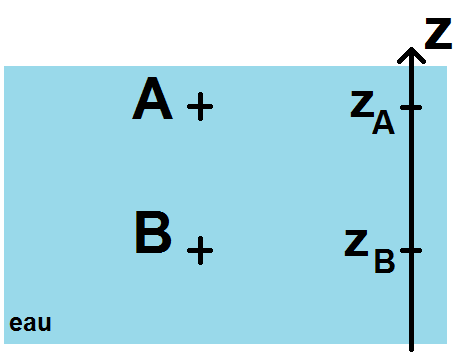
On considère la mer, avec deux points A et B.
On note PA et PB la pression en ces points, et zA et zB leur hauteur sur l’axe vertical ascendant.
D’après la LFS, on a :
\(\textstyle P_B – P_A = -\rho g(z_B – z_A) \)
\(\textstyle P_B = P_A + \rho g(z_A – z_B) \)
Or zA – zB > 0, donc PB > PA.
Cela signifie que :
—
Dans un fluide, plus on descend, plus la pression est importante.
—
C’est pour cela que les plongeurs subissent de fortes pression quand ils plongent, leurs poumons sont alors comprimés, rendant difficile la respiration. C’est pour cela également (entre autres) qu’ils ne doivent pas remonter trop rapidement à la surface mais par palier.
On peut réécrire la LFS de la manière suivante :
\(\displaystyle P_{en \, bas} = P_{en \, haut} + \rho g h \)
Attention cette formule est à manier avec précaution, elle permet uniquement de gagner du temps si tu la maîtrises.
Dans la formule, le h représente la différence de hauteur entre les 2 points considérés, cette hauteur est toujours positive.
Ainsi, dans l’exemple suivant :
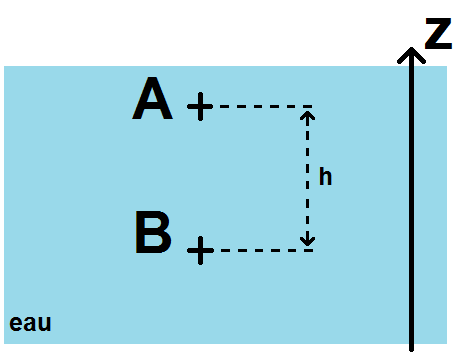
Si on cherche PB, on sait que ce sera PB = PA + ρgh et non PB = PA – ρgh car PB doit être plus grand que PA.
Dans les exercices en vidéo, nous ferons systématiquement cette petite vérification afin de vérifier la cohérence du résultat.
Par ailleurs, il existe un cas particulier très important que l’on retrouvera souvent en exercice : la pression atmosphérique, notée Patm, qui vaut environ 1 bar.
La pression atmosphérique correspond à la pression de l’air ambiant (celui que tu respires), qui peut être considérée comme constante même si l’altitude varie un peu car la masse volumique ρ de l’air est très faible.
Le principe est le suivant : la pression à la surface de séparation entre l’air et le fluide est égale à la pression atmosphérique.
Exemple :
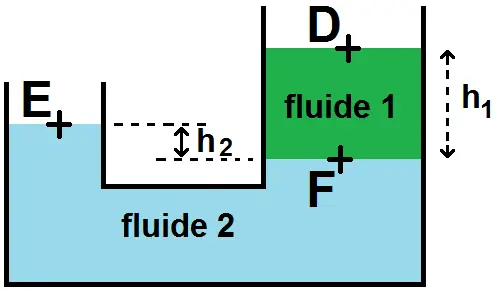
Aux points D et E, on a :
\(\textstyle P_D = P_E = P_{atm} \)
Attention cependant, D et E ne sont pas à la même altitude car ils n’appartiennent pas au même fluide.
En effet, appliquons la LFS entre D et F (qui appartiennent au fluide 1) ainsi quà E et F (qui appartiennent au fluide 2).
On obtient :
\(\textstyle P_F = P_D + \rho_1 g h_1 \)
\(\textstyle P_F = P_E + \rho_2 g h_2 \)
On a donc :
\(\textstyle P_D + \rho_1 g h_1 = P_E + \rho_2 g h_2 \)
Or on a vu que PD = PE, d’où :
\(\textstyle \rho_1 g h_1 =\rho_2 g h_2 \)
\(\textstyle \rho_1 h_1 =\rho_2 h_2 \)
Si D et E étaient au même niveau, on aurait h1 = h2, et donc ρ1 = ρ2 : si les 2 fluides ont le même ρ, les points D et E sont à la même hauteur, sinon ce n’est pas le cas.
Cela est logique, car si les 2 fluides sont identiques (ρ1 = ρ2), ils ne forment alors qu’un seul et même fluide, et les deux points seraient alors à la même hauteur :
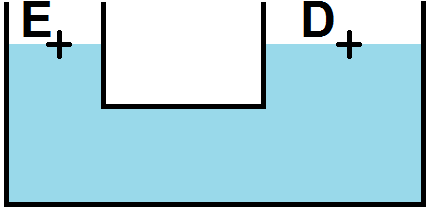
Ce que l’on vient de voir ci-dessus est un exercice très classique sur la statique des fluides (nous en ferons des similaires dans les exercices en vidéo).
Bien sûr attention, il faut qu’un point soit « à l’air libre » pour que la pression soit la pression atmosphérique.
Prenons le cas ci-dessous :
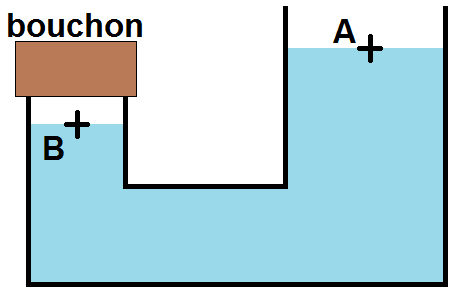
En A, le point est à l’air libre donc PA = Patm, mais en B le point n’est pas à l’air libre à cause du bouchon, donc PB ≠ Patm.
Le théorème de Pascal n’est pas très utilisé dans les exercices mais il peut t’être demandé en question de cours.
Il s’énoncé de la manière suivante :
—
Pour un fluide incompressible en équilibre , toute variation de pression en un point est intégralement transmise en tout point du fluide.
—
Autrement dit, si on fait varier la pression en un point (par application d’une force par exemple), tout autre point du fluide subira la même variation.
L’hypothèse que le fluide soit incompressible et en équilibre permet d’appliquer la LFS simplifiée.
Voyons la démonstration.
On va supposer que l’on fait varier la pression en un point A, et on va voir ce qui se passe en un point B quelconque du fluide.
On va se placer entre deux instants : avant la variation de pression (instant 1) et après la variation de pression (instant 2).
La variation de pression en A est ainsi PA,2 – PA,1 = Δ P
De plus, d’après la LFS simplifiée aux instants 1 et 2 :
PA,1 – PB,1 = -ρ g (zA – zB)
PA,2 – PB,2 = -ρ g (zA – zB)
Donc :
PA,1 – PB,1 = PA,2 – PB,2
PB,2 – PB,1 = PA,2 – PA,1 = Δ P
Ainsi, la variation en B entre les instants 1 et 2 est la même qu’en A, ce qui démontre le théorème de Pascal.
Il est maintenant temps de passer aux exercices !
Pour accéder aux exercices sur ce chapitre, clique ici !
Sommaire des coursHaut de la page



Bonjour, vraiment grand merci. Le cours est vraiment bien détaillé et bien compréhensible. J’aurais vraiment souhaité que vous m’aidiez avec la suite du cours avec des exercices à l’appui. Merci une fois de plus pour ce cours de mécanique de fluide 😊