Le phénomène de diffraction

Sommaire

Introduction
Principe général
Diffraction d’un laser avec une fente
Exercices

Introduction

Le phénomène de diffraction se produit quand une onde rencontre un obstacle ou un trou dont les dimensions sont de l’ordre ou inférieures à la longueur d’onde de l’onde.
Ce chapitre utilise beaucoup de notions vues dans le chapitre sur les ondes (longueur d’onde, célérité etc…). Il est donc fortement recommandé de bien le connaître avant d’aborder la diffraction
Nous verrons également dans ce chapitre les propriétés des lasers (on pose souvent des questions dessus !).

Principe général

On rappelle tout d’abord qu’une onde est caractérisée par :
sa longueur d’onde λ en m
sa fréquence f en Hz
sa célérité c en m.s^-1

Les trois valeurs sont reliées par la formule :

Nous allons nous intéresser essentiellement à la longueur d’onde λ de l’onde.

On va se placer dans une situation où l’onde va rencontrer une ouverture ou un obstacle.
Par exemple on envoie de la lumière sur une plaque avec un trou dessus, ou on envoie de la lumière sur un fil, ou des vagues arrivent sur une digue présentant une ouverture etc…

L’ouverture ou l’obstacle va avoir une longueur caractéristique que l’on notera toujours a.
Cela peut être le diamètre du trou, le diamètre du fil, la largeur de l’ouverture etc…
« a » étant une longueur, cette valeur sera en mètres.

La règle est la suivante :

—
Si la longueur a est de l’ordre de grandeur ou inférieure à la longueur d’onde λ, il y a phénomène de diffraction.
En revanche, si a est supérieure à λ il n’y a pas de diffraction.
—

Si on prend des vagues qui arrivent sur un mur, on obtient cela :

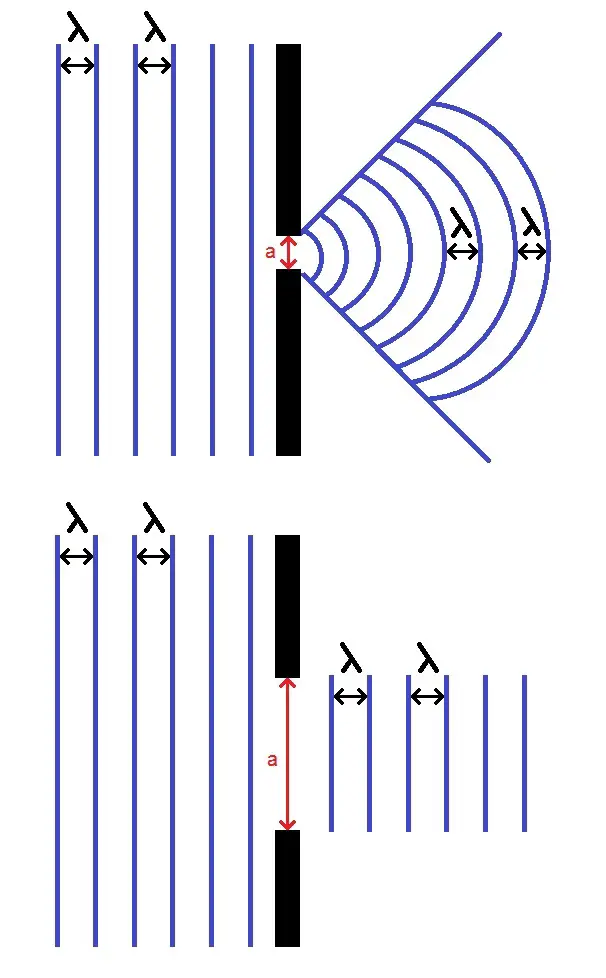
Sur le premier schéma l’ouverture a est environ égale à la longueur d’onde : il y a phénomène de diffraction, c’est-à-dire que l’onde se propage différemment après l’obstacle.
Dans le deuxième schéma en revanche, a est largement supérieure à la longueur d’onde : il n’y a pas diffraction, donc l’onde continue de se propager (mais seulement au niveau de l’ouverture, pas sur les côtés !).

Il y a une propriété qui apparaît sur les schémas : la longueur d’onde avant l’ouverture est la même qu’après l’ouverture !
Il en est de même pour la fréquence de l’onde.

—
L’onde après l’obstacle ou l’ouverture a la même longueur d’onde et la même fréquence qu’avant l’obstacle ou l’ouverture.
—

Une autre propriété de la diffraction est que le phénomène est d’autant plus important que l’ouverture ou l’obstacle est petit, c’est-à-dire que a est petit :

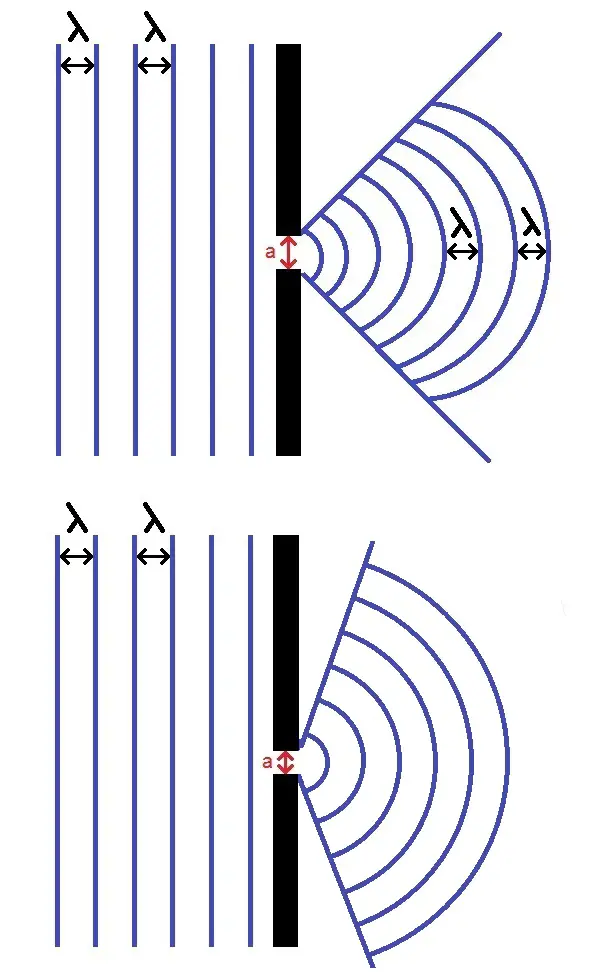
Dans le schéma du bas l’ouverture est plus petite que dans celui du haut : le phénomène de diffraction est plus prononcé.

—
Plus l’ouverture ou l’obstacle est petit, plus le phénomène de diffraction est important.
—

Le phénomène de diffraction est possible avec toutes les ondes, dont la lumière qui est une onde lumineuse.
Après les vagues, nous allons donc voir la diffraction avec la lumière qui est l’application la plus courante que tu rencontreras en contrôle et au bac.

Diffraction d’un laser avec une fente

Haut de page

Le fait que la lumière puisse subir le phénomène de diffraction est d’ailleurs une des preuves que la lumière est bien une onde !
En contrôle ou au bac, tu pourras avoir la question « quel caractère de la lumière l’apparition d’une figure de diffraction met-elle en évidence ? » (question du bac de septembre 2011 aux Antilles).
La réponse est que la diffraction met en évidence le caractère ondulatoire de la lumière, c’est-à-dire le fait que la lumière soit une onde.

La plupart des exercices font intervenir une onde particulière : l’onde laser, émise par un laser.
Le laser a trois propriétés à connaître ABSOLUMENT car cela peut t’être demandé (par exemple question du bac 2017 Amérique du Nord : « rappeler les trois principales propriétés du faisceau d’un laser ») :
– la lumière est monochromatique (constituée d’une seule longueur d’onde) ;
– la lumière est directive : le faisceau lumineux se propage dans une seule direction ;
– la lumière est cohérente : les ondes émises sont en phase.

Ces trois propriétés sont à apprendre PAR CŒUR !!!

Mais il n’y a pas que ça à connaître !

On va effectuer la diffraction d’un laser par une fente verticale de largeur « a » et regarder ce que l’on obtient sur un écran.
Le schéma est le suivant :

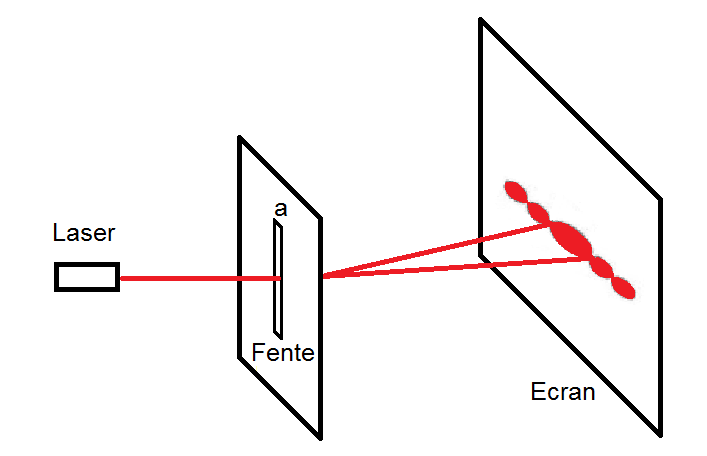
Comme tu le vois la figure obtenue n’est pas une fente verticale mais un ensemble de taches, de plus en plus petites au fur et à mesure que l’on s’éloigne de la tache centrale.
Tu remarqueras que la fente est verticale mais les taches sont horizontales.
Si la fente avait été horizontale, les taches auraient été verticales…

Evidemment, comme dit plus haut, il faut que la largeur « a » de la fente soit petite devant la longueur d’onde λ.
Plus la fente sera petite plus le phénomène de diffraction sera prononcé. C’est ce que l’on va montrer par le calcul !

Pour cela, schématisons le dispositif non pas en 3D comme ci-dessus mais vu de côté.
On prendra une fente horizontale pour avoir des taches verticales. On a alors le schéma suivant :

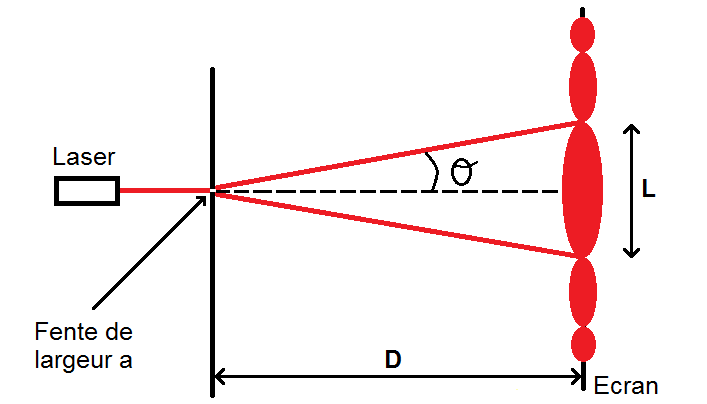
On note D la distance entre la fente et l’écran.
« a » la largeur de la fente, en m.
L le diamètre de la tache centrale, en m
λ la longueur de l’onde, en m.
θ l’angle entre l’axe central et une extrémité de la tache centrale, en radians : c’est ce que l’on appelle l’écart angulaire.

Il y a une formule que tu ne peux pas deviner et que tu dois donc connaître par cœur :

Il y a une autre formule en revanche que tu dois savoir redémontrer comme on va le faire.
Mettons nous dans le triangle rectangle mis en vert sur ce schéma :

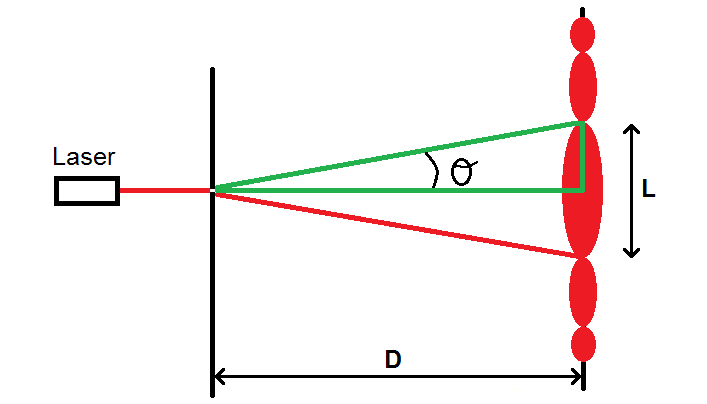
Avec la trigonométrie, on a :

Or θ est un angle petit, on peut donc approcher tan(θ) par θ : tan(θ) ≈ θ
D’où :

Ainsi, on voit que plus a est petit, plus L est grand, c’es-à-dire que la tache centrale sera plus grande et donc que le phénomène de diffraction sera plus important : cela est logique avec ce que l’on a dit précédemment !

La petite démonstration que l’on vient de faire permet de trouver une relation entre différentes grandeur : L, D, λ et a.
Cela peut très bien servir à calculer une de ces quatre grandeurs en connaissant les trois autres, il faut donc que tu saches retrouver cette formule.

—
ATTENTION cependant !!
Dans les schéma on a considéré que L était le diamètre de la tache centrale. Mais il peut arriver que L soit le rayon de la tache centrale !
On peut donc avoir une formule du style (entraîne toi à faire la démonstration) :

Comme tu le vois le 2 du dénominateur a disparu.
Il faut donc adapter la démonstration précédente à l’énoncé qui te sera donné.
—

Ce que l’on vient de voir avec une fente (donc une ouverture) est également vrai pour un obstacle !
L’exemple le plus classique est le cheveu : le rayon laser va arriver sur le cheveu et on aura le même type de figure de diffraction à savoir une tache centrale et des taches de part et d’autre.
Le « a » représente alors le diamètre du cheveu : ce diamètre doit être petit devant la longueur d’onde.

L’intérêt est que, comme on l’a vu, on peut calculer le a avec la formule, donc on peut calculer le diamètre d’un cheveu !

Il est possible que tu fasses l’expérience en TP :
– tu connais la longueur d’onde λ du laser (écrite sur le laser par exemple ou dans la documentation) ;
– tu peux mesurer la distance D entre le cheveu et l’écran ;
– tu peux mesurer le diamètre L de la tache centrale.

Il ne reste plus qu’à isoler a dans la formule vue précédemment :

On remplace, et le tour est joué !

Tu sais maintenant tout sur la diffraction, il est temps de passer aux exercices pour t’entraîner !

Exercices

Haut de page

Les exercices seront bientôt disponibles !

Sommaire des coursHaut de la page