Sommaire
Introduction
Principes et définitions
Ondes longitudinales et transversales
Célérité d’une onde
Périodes spatiale et temporelle
Fréquence de l’onde
Exercices
Nous allons voir dans ce chapitre les définitions, formules, et calculs entre autres qui sont en relation avec les ondes. Ce chapitre est la base pour comprendre d’autres chapitres liés aux ondes.
Nous allons prendre un exemple pour comprendre ce qu’est une onde.
Prenons un ressort. Si on ne le touche pas il restera au repos, il ne se passera rien.
Mais si on tire dessus à une extrémité, on fait ce que l’on appelle une perturbation, c’est-à-dire que l’on perturbe sa position de repos.
Cette perturbation va se propager le long du ressort et celui-ci va se mettre à osciller en se comprimant et en s’étirant.
Une onde, c’est ce phénomène de perturbation qui se propage, ici dans un ressort mais cela peut-être dans l’eau, dans une corde, une table, et même dans l’air (que l’on peut assimiler à du vide).
On appelle cela une onde progressive (car la perturbation progresse en se propageant).
On distingue alors deux types d’ondes progressives :
– les ondes mécaniques qui nécessitent un milieu matériel pour se propager (un ressort, de l’eau, une table etc…)
– les ondes électromagnétiques (comme la lumière) qui peuvent se propager dans le vide et n’ont pas forcément besoin de milieu matériel.
Par ailleurs, il faut bien noter que ce n’est pas la matière qui se propage mais l’énergie. La perturbation initiale a en effet créé de l’énergie et c’est cette énergie qui se diffuse en se propageant.
A partir de tous ces éléments on peut donner la définition d’une onde mécanique progressive
—
Une onde mécanique progressive est le phénomène de propagation d’une perturbation dans un milieu matériel, sans transport de matière mais avec transport d’énergie.
—
Si on te demande juste la définition d’une onde progressive (sans préciser mécanique), c’est la même chose mais il faut enlever « dans un milieu matériel » :
—
Une onde progressive est le phénomène de propagation d’une perturbation, sans transport de matière mais avec transport d’énergie.
—
Il est très fréquent en contrôle et au bac de demander la définition d’une onde mécanique progressive donc après bien cette définition ! 
A noter que dans une question, le mot « progressive » peut ne pas être marqué : cela revient au même. On peut donc te demander la définition d’une onde mécanique (évidemment tu écris la définition donnée ci-dessus).
Par ailleurs, les ondes se propagent dans toutes les directions qui leur sont offertes. Elles peuvent donc être à une, deux ou trois dimensions. Donnons un exemple pour chacun de ces types d’ondes :
– onde à une dimension : onde le long dune corde ou d’un ressort
– onde à deux dimensions : onde à la surface de l’eau après avoir jeté un caillou dans l’eau
– onde à trois dimensions : onde sonore, par exemple un son créé par une enceinte qui se propage dans toute la pièce
Il est possible en contrôle que l’on te demande un exemple de chaque type d’onde (retiens donc bien ces exemples  ).
).
Les ondes se divisent en d’autres catégories : les ondes transversales et longitudinales.
Pour distinguer les deux, tout va se jouer sur la direction de la perturbation, et la direction de la propagation de l’onde.
Prenons un ressort que l’on étire en exerçant une force F horizontale, qui correspond à la perturbation :
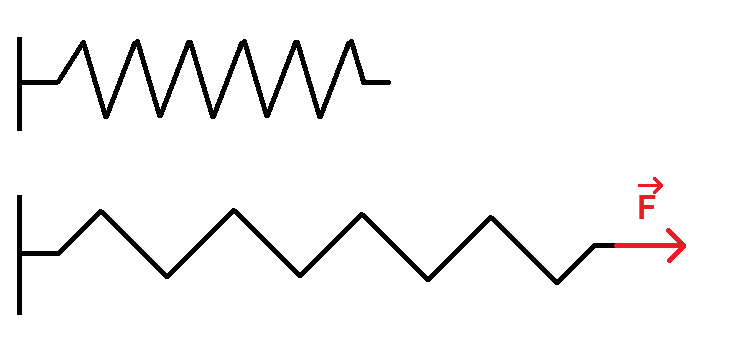
La direction de la perturbation (la force F) est horizontale.
Cette perturbation va se propager horizontalement également (le long du ressort).
La direction de la propagation est la même que celle de la perturbation : c’est une onde longitudinale.
Si au contraire la direction de la perturbation est perpendiculaire à la direction de la propagation, c’est une onde transversale.
C’est le cas par exemple d’un caillou que l’on jette dans l’eau (perturbation verticale) mais l’onde se propage dans l’eau de manière horizontale (en faisant des cercles concentriques) :

La goutte tombe verticalement (perturbation) mais l’onde se propage horizontalement à la surface de l’eau : c’est une onde transversale.
On peut donc donner les définitions suivantes :
—
Une onde est longitudinale si la direction de la propagation est la même que la direction de la perturbation.
—
—
Une onde est transversale si la direction de la propagation est perpendiculaire à la direction de la perturbation.
—
Très souvent ces définitions sont demandées au bac et en contrôle !!!
A noter que pour une onde longitudinale, on peut dire également que la direction de la perturbation est parallèle à la direction de la perturbation (ce qui donne la même définition que pour l’onde transversale mais avec parallèle à la place de perpendiculaire).
La célérité d’une onde est tout simplement sa vitesse. Elle peut être notée v (comme vitesse) mais aussi c (comme célérité), tout dépend de l’énoncé.
Souvent dans les exercices le c correspond à une constante qui est la célérité de la lumière dans le vide (3,00 x 108 m.s-1), nous appellerons donc la célérité v dans les formules qui suivent.
La célérité d’une onde étant constante, on peut appliquer la formule que l’on connaît depuis le collège :
\(\displaystyle v = \frac{d}{t} \)
d correspond à la distance (en m, ou km, ou mm etc…)
t correspond au temps (en s, h, min etc…)
v est la vitesse, son unité dépend de celle de d et t : si d est en m et t en s, v sera en m.s-1.
Si au contraire d est en km et t en h, v sera en km.h-1 etc…
Tout est possible du moment que l’on respecte cette logique des unités !
—
ATTENTION !! La formule v = d/t ne s’utilise que si la vitesse v est CONSTANTE !!
—
Pour les ondes périodiques, on peut notamment calculer la vitesse en utilisant la période spatiale notée λ et la période temporelle notée T :
\(\displaystyle v = \frac{\lambda}{T} \)
Voyons plus en détails ces périodes spatiale et temporelle.
Une onde périodique a en effet la particularité d’avoir ce que l’on appelle une double périodicité, c’est-à-dire qu’elle possède une période spatiale ET une période temporelle.
La période spatiale est notée λ (en m) et la temporelle notée T (en s).
La période spatiale est aussi appelée longueur d’onde.
Ainsi, quand on parle de période tout court, on sous-entend la période temporelle. Quand on veut parler de la période spatiale on dit longueur d’onde.
Prenons une onde se propageant le long d’une corde.
On peut tracer l’amplitude de cette onde par rapport à une variable x (qui correspond à une position), mais on peut également tracer l’amplitude de l’onde en un point de la corde au cours du temps.
On obtiendrait par exemple les graphiques suivants :
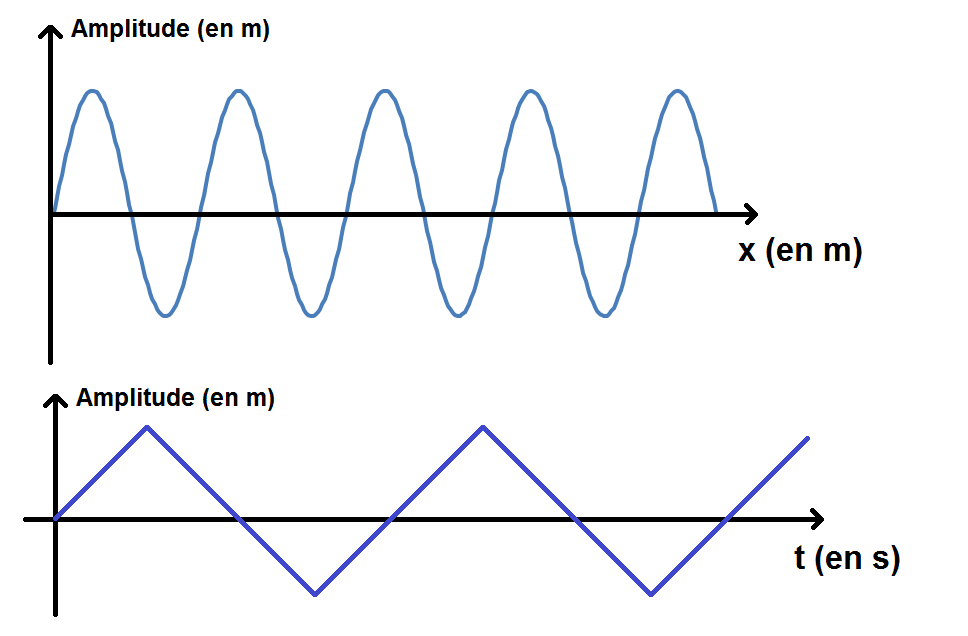
Tu remarques que la variable en abscisse n’est pas la même : x dans un cas et t dans l’autre !
Les deux courbes peuvent ne pas avoir la même forme comme c’est le cas ici.
Cependant les deux courbes sont périodiques et il existe donc deux périodes : spatiale (la longueur d’onde, quand l’abscisse est x) et temporelle (quand l’abscisse est t) :
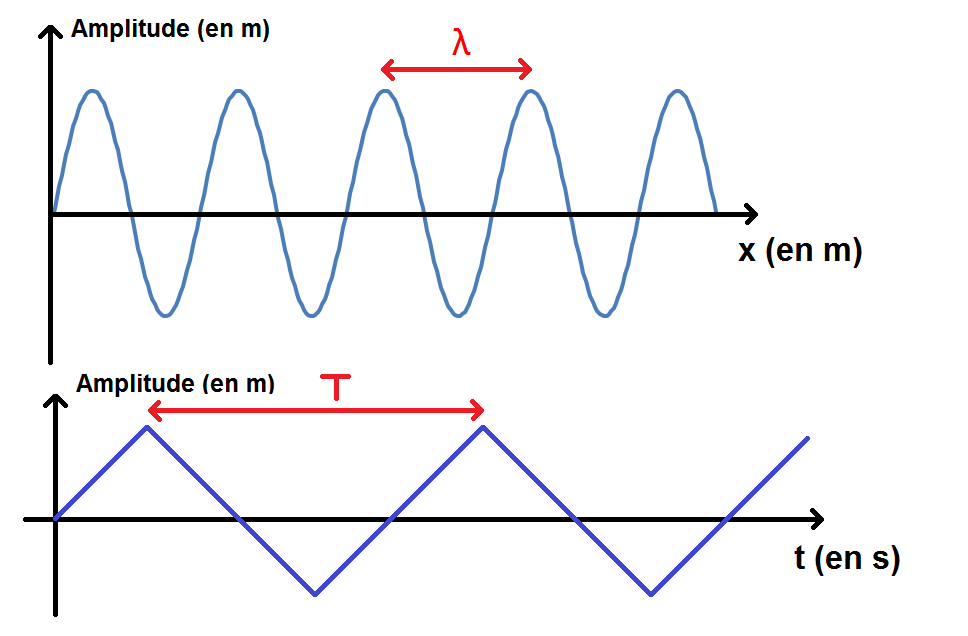
Très souvent, à partir d’un tel graphique, on te demandera de trouver la période (spatiale ou temporelle suivant le graphe que tu as).
Pour ce faire on pourrait mesurer une période, mais pour plus de précision, il faut mesurer plusieurs périodes et diviser par le nombre de périodes afin d’augmenter la précision.
Prenons cet exemple :
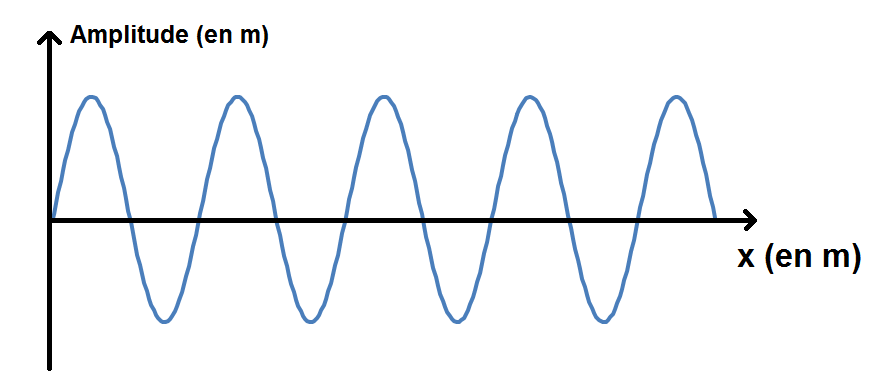
On demande de calculer la longueur d’onde de l’onde, c’est-à-dire la période spatiale (normal puisque l’on a l’amplitude en fonction de x).
Tout d’abord qu’est-ce-qu’une période ?
Une période c’est le plus petit motif qui se répète au cours du temps. Le mieux est de la prendre entre deux maximum (en rouge) ou entre deux minimum (en vert) :
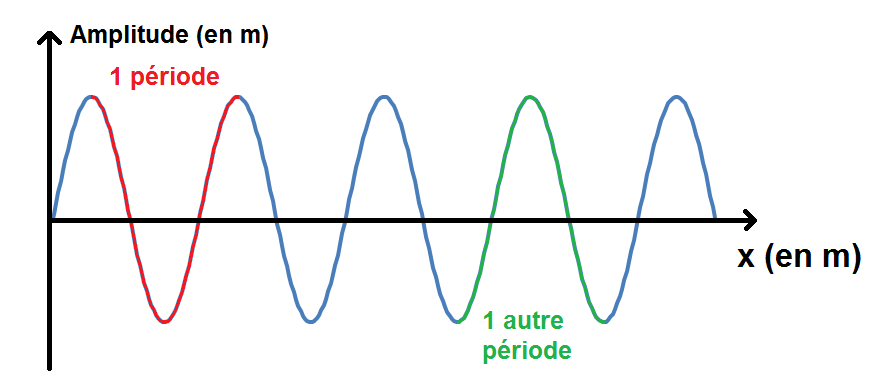
On peut également prendre une période au niveau du 0 (mais attention la période ne sera pas entre deux 0 !) :
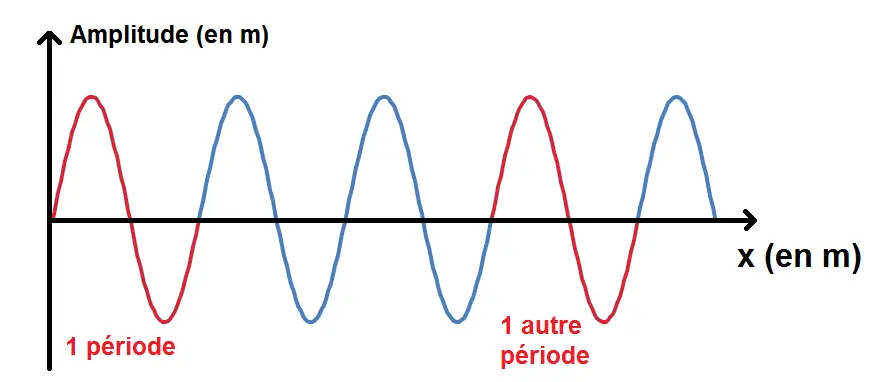
Afin de calculer au mieux la période, prenons plusieurs périodes :
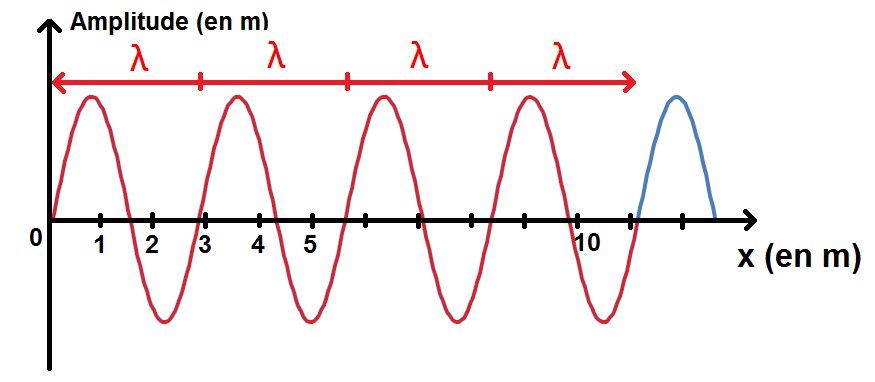
On voit que 4λ représentent 11,1 m.
Donc λ = 11,1/4
λ = 2,78 m
La précision dépendra évidemment du graphique que tu as, généralement tu as des carreaux pour t’aider.
—
Retiens bien que pour mesurer graphiquement une période on prend plusieurs périodes et on divise par le nombre de périodes afin de gagner en précision !
—
Si on te demande souvent de mesurer la période, on peut également te demander de calculer la fréquence.
Tout d’abord, sache que la fréquence est uniquement liée à la période temporelle T, pas à la longueur d’onde !!
La fréquence correspond au nombre de périodes qu’il y a dans 1 seconde (cela ne tombe donc pas forcément pile…).
On a les formules suivantes :
\(\displaystyle f = \frac{1}{T} \)
\(\displaystyle T = \frac{1}{f} \)
Il s’agit évidemment de la même formule mais écrite sous deux formes différentes.
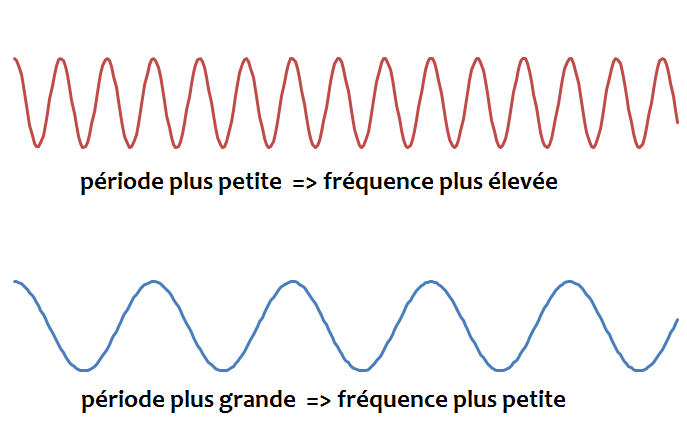
On voit que la fréquence est inversement proportionnelle à la période et réciproquement.
Ainsi, plus la période augmente, plus la fréquence diminue.
Plus la fréquence augmente, plus la période diminue:
Au niveau des unités, T étant en secondes (s), f est en s-1
Mais la fréquence a également une autre unité : le hertz, noté Hz.
Ainsi Hz et s-1 sont la même unité !
Cependant, quand tu appliques la formule, il faut ABSOLUMENT respecter ces unités !! C’est-à-dire mettre f en Hz et T en s.
Si tu as T en heures ou en minutes ou millisecondes par exemple, ou f en kilohertz (kHz), il faut toujours convertir en s et en Hz.
Cela est donc différent de la formule v = d/t où l’on n’est pas obligé de convertir du moment que c’est cohérent.
—
Quand on applique la formule T = 1/f ou f = 1/T, il faut toujours mettre T en s et f en Hz.
—
Enfin, pour terminer avec la fréquence, revenons à une formule vue précédemment :
On a donc une autre formule pour la vitesse :
\(\displaystyle v = \lambda \times f \)
Tu appliqueras la formule v = λ/T ou v = λf suivant ce que tu as ou ce que tu recherches dans l’énoncé (T ou f).
Avec tout ce que l’on a vu tu devrais être capable de faire la plupart des exercices sur les ondes !
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !
Sommaire des coursHaut de la page



J’ai aimé ce site!!!
merci cours très bien expliqué
C’est bien comme cours cependant, certaines images ne chargent pas sur le site web. Merci beaucoup pour ces cours éppurrés et simple de compréhension !
merciiiiiiiiiiii