Les lois de Newton

Sommaire

Introduction
La notion de référentiel
Première loi de Newton : principe d’inertie
Deuxième loi de Newton : principe fondamental de la dynamique
Troisième loi de Newton : principe des actions réciproques
Les différents types de mouvement
Exercices

Introduction

Nous allons voir dans ce chapitre les lois de Newton, du nom du célèbre mathématicien et physicien anglais Isaac Newton.
Il y a 3 lois de Newton : la première, la deuxième… et la troisième ! Elles ont toutes un nom relatif à la loi qu’elles énoncent.
Ces lois sont importantes car ce sont elles, entre autres, qui permettent de résoudre les exercices de mécanique. On s’en servira notamment dans le chapitre sur les équations horaires ainsi que le chapitre sur les lois de Kepler.
Ce chapitre sur les lois de Newton constitue, avec le chapitre sur le poids, la base de la mécanique.

Retiens bien l’énoncé de chaque loi car cela peut t’être demandé comme question de cours dans un contrôle !

Avant de parler des lois en elles-mêmes, il faut que l’on aborde la notion de référentiel.

La notion de référentiel

Pour comprendre la notion de référentiel nous allons parler de la vitesse.
Imaginons que tu sois assis dans un train roulant à 50 km.h^-1 en train de regarder le paysage.
Quelle est ta vitesse ?
Tout dépend du référentiel !

En effet, tu bouges par rapport au paysage, ce pourquoi celui-ci défile devant tes yeux. On peut dire également que tu bouges par rapport aux rails, à la même vitesse que le train : ta vitesse par rapport aux rails est de 50 km.h^-1.
Mais ta vitesse par rapport au train est de… 0 km.h^-1 !
En effet, tu es immobile par rapport au train, c’est comme si tu étais attaché au train (en tout cas tant que tu restes assis et que tu ne te balades pas dans le train).

Ta vitesse est donc différente par rapport au train et par rapport aux rails : le train ou les rails dans cet exemple est ce qu’on appelle un référentiel.
Ta vitesse dans le référentiel du train est de 0 km.h^-1 mais ta vitesse dans le référentiel des rails est de 50 km.h^-1.

En fait, n’importe quel objet peut être un référentiel, toi-même tu peux être un référentiel !

A noter qu’évidemment, dans un référentiel, le référentiel en lui-même est immobile.
Par exemple dans le référentiel du train, le train est immobile, dans le référentiel d’une planète, la planète est immobile.

Une planète peut en effet également être un référentiel.
C’est d’ailleurs les planètes qui seront souvent utilisées dans les exercices !

En effet, il y a 3 référentiels particuliers que tu dois connaître par cœur :
– le référentiel héliocentrique (du grec hélios : le Soleil), qui est un référentiel centré sur le Soleil et dont les axes pointent des étoiles fixes. Ce référentiel est utilisé pour étudier le mouvement des planètes autour du Soleil (comme la Terre par exemple).
– le référentiel géocentrique (du grec geos : la Terre) : il est centré sur la Terre mais, comme précédemment, ses axes pointent vers des étoiles fixes : les axes ne tournent pas en même temps que la Terre. Ce référentiel est utilisé pour étudier le mouvement des satellites autour de la Terre, dont la Lune.
– le référentiel terrestre, lui aussi centré sur la Terre mais dont les axes bougent en même temps que la rotation de la Terre sur elle-même. Ce sera le référentiel le plus souvent utilisé.

Il existe également des référentiels saturno-centrique (centré sur Saturne), mercuro-centrique (centré sur Mercure) etc… mais tu n’as pas à les connaître.

Les trois référentiels cités ci-dessus ont la particularité d’être des référentiels galiléens.
Mais qu’est-ce-qu’un référentiel galiléen ??
C’est ce que l’on va voir avec la première loi de Newton !

Première loi de Newton : principe d’inertie

Haut de page

La première loi de Newton, aussi appelée principe d’inertie, peut être définie de la manière suivante :

—
Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme dans lequel il se trouve si et seulement si les forces extérieures appliquées sur lui se compensent.
—

Qu’est-ce-que c’est que ce charabia ??

Reprenons la phrase dans l’ordre :
– le « corps » est le système que l’on considère. On commencera en effet tous les exercices de mécanique en parlant de quel système on parle, par exemple si on étudie une voiture, considère-t-on toute la voiture ? Que les roues ? Que le volant ? etc…
– « l’état de repos », c’est quand le système est immobile. Pour le mouvement rectiligne uniforme en revanche, le système va en ligne droite (rectiligne) et à vitesse constante (uniforme). Par exemple une voiture qui roule sur une route droite à la même vitesse.
– « dans lequel il se trouve » signifie que l’on regarde l’état du système à l’instant initial, à t = 0 s.
– « forces extérieures » signifie que l’on ne prend pas en compte les forces internes : si on prend comme système toute la voiture avec le conducteur et les passagers, on ne prendra pas en compte la force de la ceinture sur le conducteur par exemple.
– « se compensent » signifie que la somme des vecteurs forces est égal à vecteur nul (pas 0 !!!).
En effet, les forces sont représentées par des vecteurs, qui peuvent s’additionner comme en maths, et le résultat peut être le vecteur nul (pas 0 !)

Le « si et seulement si » signifie que la loi marche dans les deux sens :
– si le système est immobile ou en mouvement rectiligne uniforme, alors on peut dire que les forces extérieures se compensent.
– si les forces extérieures se compensent, alors on peut dire que le système est immobile ou en mouvement rectiligne uniforme.

Bon c’est très bien tout ça mais quel est le rapport avec les référentiels galiléens ??

—
Un référentiel est dit galiléen si le principe d’inertie y est vérifié.
—

Ainsi, si dans un référentiel le principe d’inertie énoncé ci-dessus est vérifié, alors ce référentiel est galiléen, sinon il ne l’est pas.

Les référentiels héliocentrique, géocentrique et terrestre dont on a parlé précédemment sont des référentiels galiléens, ou supposés galiléens. Dans les exercices on te dira en effet « on travaille dans le référentiel terrestre supposé galiléen ».

Avec tout ce que l’on vient de voir, la première loi de Newton peut s’exprimer de manière différente :

—
Dans un référentiel galiléen, la somme des forces extérieures appliquées à un système est nulle si et seulement si ce système est au repos ou en mouvement rectiligne uniforme.
—

Tu peux apprendre ce nouvel énoncé, il est plus facile à retenir

Mais concrètement, que signifie que les forces extérieures se compensent, ou que la somme des forces extérieures appliquées au système est nulle ?
Nous allons voir cela avec des schémas.
Nous allons prendre comme système une balle.
Si le système n’est soumis à aucune force :

Rien de particulier, il n’y a aucune force : donc leur somme est nulle !

Le système ne peut pas être soumis à une seule force, car une force (un vecteur) additionné avec rien d’autre ne peut pas donner le vecteur nul…

Si le système est soumis à deux forces : ces deux forces doivent être de même direction, de même intensité (même norme) mais de sens opposé !
En effet, si on a deux forces F₁ et F₂ qui se compensent :

donc

Ainsi les deux vecteurs forces sont opposés, donc comme dit précédemment, même direction, même norme mais sens opposé !
On peut alors avoir par exemple les schémas suivants :

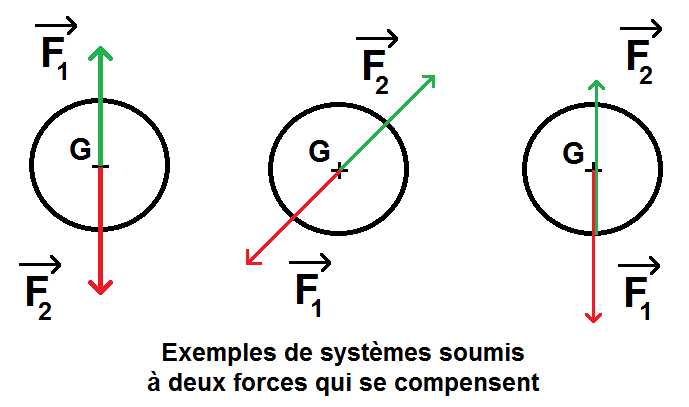
En revanche, comme on le voit dans le troisième exemple, le point d’application des forces n’est pas forcément le même : certaines peuvent s’appliquer au centre de gravité G du système (comme le poids), d’autres peuvent s’appliquer à la surface du système comme les forces de frottement, cela n’a aucune importance !

Nous allons enfin voir un exemple de ce que cela donne avec 3 forces :

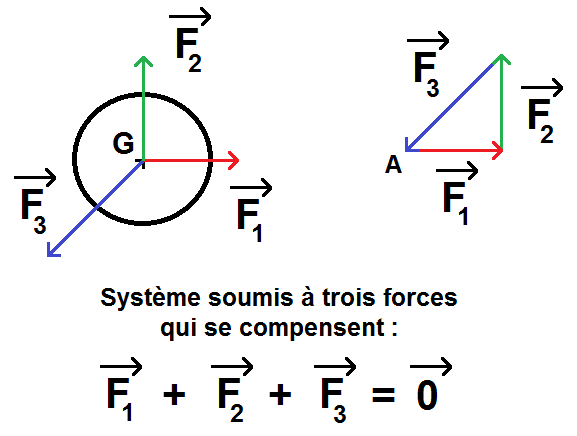
Ici on a reporté les vecteurs sur le côté en partant du point A afin de les additionner pour les mettre bout à bout, et on voit qu’on revient au point de départ A.
On a donc :

Les forces se compensent !
On peut donc appliquer dans chacun des cas précédents le principe d’inertie.

Nous verrons des exemples d’application dans les exercices.

Deuxième loi de Newton : principe fondamental de la dynamique

Haut de page

La première loi de Newton est en fait un cas particulier de la deuxième loi de Newton, aussi appelée PFD (principe fondamental de la dynamique).
En effet, de manière générale, les forces ne se compensant pas nécessairement, et on a la relation suivante correspondant à la deuxième loi de Newton, uniquement valable dans un référentiel galiléen :

—
ATTENTION !! Dans cette formule le vecteur p correspond à la quantité de mouvement, pas au poids, ce pourquoi il est noté avec p minuscule alors que le poids est noté avec un P majuscule.
—

Cette formule constitue la deuxième loi de Newton, qui peut se mettre sous forme de phrase :

—
Dans un référentiel galiléen, la somme vectorielle des force extérieures exercées sur un système est égale à la dérivée du vecteur quantité de mouvement de ce système par rapport au temps.
—

Mais qu’est-ce-que c’est que ce vecteur quantité de mouvement ?
Ce vecteur est égal au produit de la masse par le vecteur vitesse du système :

Oui mais quelle vitesse ? Car on a dit que la vitesse dépendait du référentiel !
Tout simplement la vitesse dans le référentiel que tu auras explicité dans la rédaction.

En effet, avant d’appliquer la deuxième loi de Newton, comme celle-ci s’applique uniquement dans les référentiels galiléens, la rédaction sera :
« On applique la deuxième de Newton au système … dans le référentiel galiléen … » : tu remplaceras évidemment les trois petits points par le bon référentiel, par exemple le référentiel terrestre ou géocentrique.
La vitesse sera alors celle exprimée dans ce référentiel.

Remplaçons alors le vecteur p dans la formule :

Or la masse étant constante, on peut sortir le m de la dérivée :

or

d’où

Apprends bien ce calcul par cœur car tu devras le refaire tout le temps quand tu appliqueras la deuxième loi de Newton !!
En effet, le vecteur accélération est plus intéressant que le vecteur quantité de mouvement car on a les relations suivantes :

et

Autrement dit, l’accélération est la dérivée de la vitesse par rapport au temps, et la vitesse est elle-même la dérivée de la position (le point M étant le point définissant la position du système).

Ainsi, en faisant la primitive comme on le verra dans le chapitre sur les équations horaires, l’accélération nous permettra d’obtenir la vitesse puis la position.

—
Remarque : dans la démonstration, on a sorti la masse de la dérivée car on a dit qu’elle était constante. Ce sera le cas dans la quasi-totalité des exercices.
Cependant, il existe des exercices où ce n’est pas le cas, le plus classique étant l’étude d’une fusée qui décolle et qui brûle beaucoup de carburant, la masse de carburant diminue donc la masse totale aussi : nous étudierons ce cas particulier dans les exercices.
—

Une fois que l’on a fait le petit calcul précédent on a une égalité vectorielle que l’on va utiliser pour trouver des relations entre les différentes données de l’énoncé.
Nous verrons cela en détail dans les exercices.

Passons désormais à la troisième loi de Newton !

Troisième loi de Newton : principe des actions réciproques

Haut de page

La troisième loi de Newton, appelée principe des actions réciproques, peut se traduire par l’égalité suivante :

F_A/B représente la force exercée par un objet A sur un objet B, tandis que F_B/A représente la force exercée par un objet B sur un objet A.

Prenons un exemple : imaginons que tu appuies vers le bas sur une table avec ta main : il y a une force exercée par ta main sur la table F_main/table.
En réaction, la table va exercer une force sur ta main F_table/main.
Ces deux forces auront même direction, même norme mais des sens opposés :

Cela se traduit graphiquement de la manière suivante (la main n’a pas été représentée^^) :

—
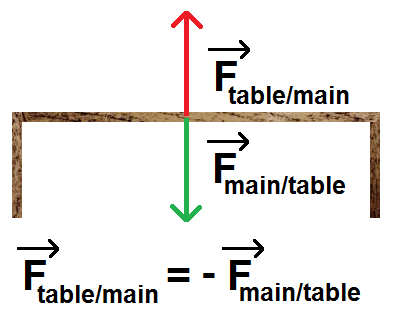
Attention à ne pas confondre inverse et opposé !
L’inverse de A, c’est 1/A.
L’opposé de A, c’est -A.
Ainsi, ici les forces sont opposées, pas inverses…
—

Autre exemple basique : si un objet est immobile et posé sur une surface plane, il exerce une force sur cette surface correspondant à son poids. En réaction la surface exerce une force sur l’objet égale à l’opposée de cette force, donc à l’opposé du poids :

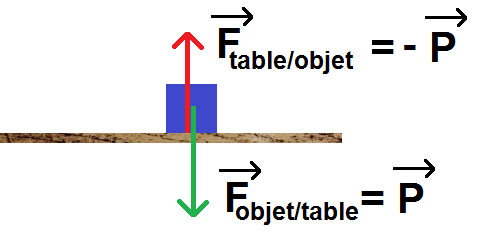
Grâce au principe des actions réciproques, on peut connaître la force de la table sur l’objet qui est l’opposé du poids.

Nous verrons des exemples d’application dans les exercices.
Mais avant de passer aux exercices, voyons une dernière chose : les différents types de mouvements que l’on peut rencontrer.

Les différents types de mouvement

Haut de page

Quand dans un exercice on te demande de décrire un mouvement, il faut préciser sa trajectoire ainsi que la variation de sa vitesse.

La trajectoire correspond au trajet que suit le système, cela peut être une droite, un cercle, une ellipse, ou toute autre forme géométrique, voire une forme quelconque !
On distingue trois grands types de trajectoire que tu verras tout le temps dans les exercices :
– la trajectoire rectiligne : le système décrit une ligne droite (une voiture qui roule sur un ligne droite par exemple)
– la trajectoire circulaire : le système décrit un cercle (un enfant sur un manège par exemple)
– la trajectoire curviligne : le système ne décrit pas une trajectoire précise mais effectue des courbes.

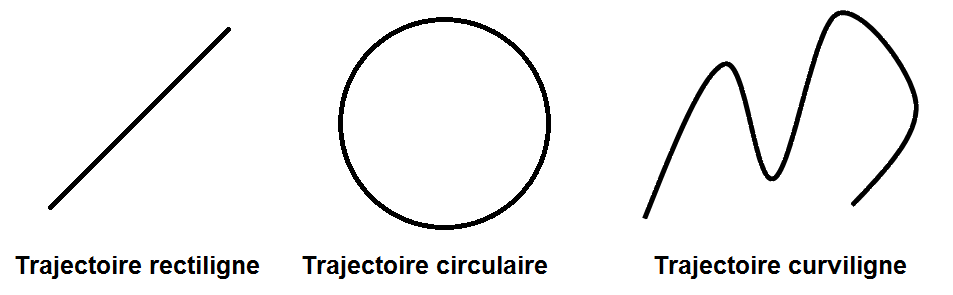
Il existe évidemment d’autres types de trajectoire : si le système décrit une ellipse, on parlera de trajectoire elliptique etc… mais les 3 que tu rencontreras le plus souvent sont celles citées ci-dessus.

Il faut désormais parler de la vitesse.
– Si la vitesse est constante, on dit que le mouvement est uniforme.
– Si la vitesse augmente, on dit que le mouvement est accéléré.
– Si la vitesse diminue, on dit que le mouvement est décéléré.

Si l’on n’est dans aucun des 3 cas précédents, on peut dire que le mouvement est aléatoire, mais cela ne devrait pas arriver…

Mais comment savoir dans quel cas l’on est ??
Si c’est dit dans l’énoncé, c’est facile^^
Si on sait que les forces se compensent, on peut appliquer le principe d’inertie vu précédemment et en déduire que le mouvement est rectiligne uniforme.

Sinon on peut te donner un enregistrement des différentes positions du système à intervalles de temps régulier et tu peux en déduire le type de mouvement.
Le principe est alors le suivant :

—
Si les points sont espacés de la même distance, le mouvement est uniforme.
Si les points sont de plus en plus rapprochés, le mouvement est décéléré.
Si les points sont de plus en plus éloignés, le mouvement est accéléré.
—

Graphiquement cela se traduit de la manière suivante pour les mouvements rectilignes :

Et pour les mouvements circulaires :

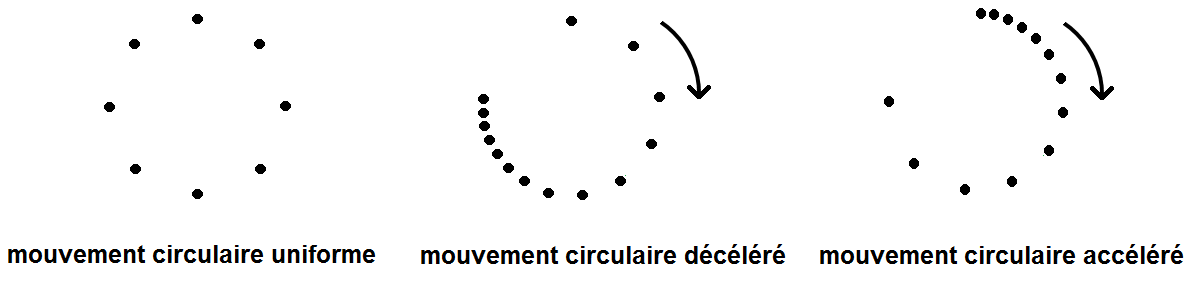
Remarque : le sens du mouvement, repéré par des flèches sur les schémas, est important pour les mouvements accélérés et décélérés car si on allait dans l’autre sens le mouvement ne serait pas accéléré mais décéléré et réciproquement…
Autre remarque : pour la trajectoire circulaire, le système n’est pas obligé de décrire tout le cercle comme on le voit sur les deux derniers schémas.

Le cas le plus intéressant et le plus courant dans les exercices est le premier, le mouvement rectiligne uniforme, car on peut appliquer la 1ère loi de Newton (principe d’inertie) contrairement aux autres cas.
Ainsi il n’y a que dans le premier cas que les forces extérieures appliquées au système se compensent (d’après le principe d’inertie).

Il est temps désormais de passer aux exercices !

Exercices

Haut de page

Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !