Sommaire
Introduction
Vocabulaire
1ère loi de Descartes
2ème loi de Descartes : la réflexion
3ème loi de Descartes : la réfraction
La réflexion totale
Exercices
Dans ce cours nous allons voir les lois de Descartes, aussi appelées lois de Snell-Descartes. Elles sont au nombre de trois, et font partie des lois de base en optique.
Comme il y a beaucoup de vocabulaire, nous allons dans un premier temps voir tout ce vocabulaire puis étudier chacune de ces lois.
Nous terminerons évidemment par des exercices 
Dans ce chapitre nous allons étudier ce qu’il se passe quand un rayon lumineux arrive sur une surface séparant deux milieux différents.
Par exemple l’air et du verre, ou l’air et de l’eau, ou du verre et de l’eau etc…
Cette surface séparatrice est appelée dioptre.
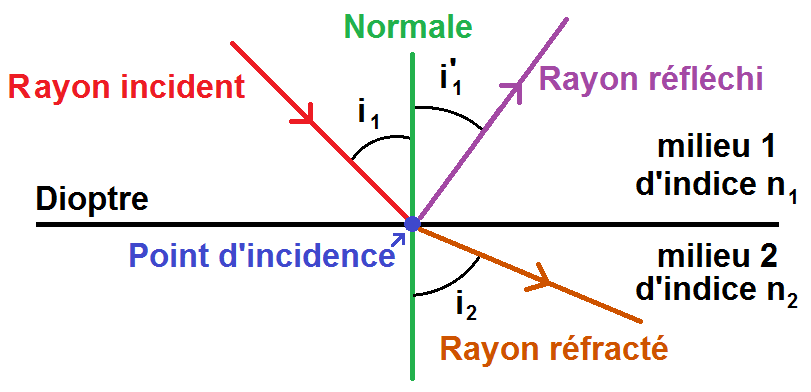
Le rayon lumineux qui arrive sur cette surface est appelé rayon incident.
Nous appellerons milieu 1 le milieu dans lequel se trouve le rayon incident et milieu 2 l’autre milieu.
Le schéma de base est pour l’instant celui-ci (nous le compléterons par la suite) :
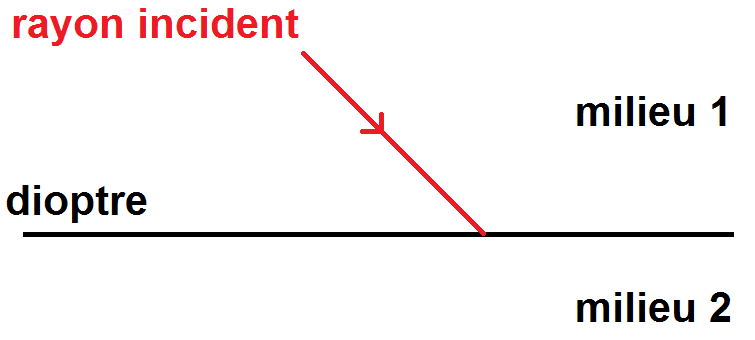
Ne pas oublier de mettre la flèche sur le rayon incident pour indique le sens
Le rayon arrive sur le dioptre en un point : ce point est appelé point d’incidence.
A partir de ce point, on peut tracer la droite perpendiculaire au dioptre passant par ce point : cette droite est appelée la normale (en géométrie, normal signifie perpendiculaire).
Le schéma se complète ainsi :
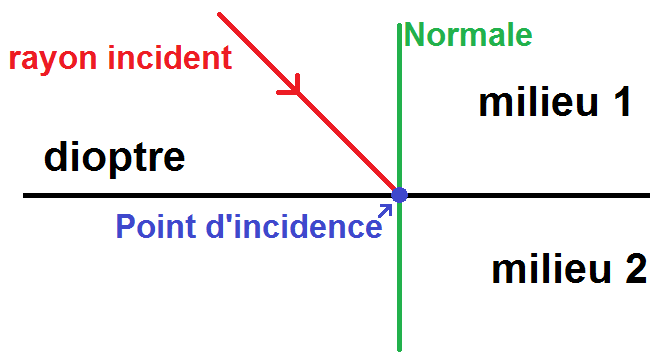
Une fois que le rayon sera arrivé au point d’incidence, 2 solutions :
– soit le rayon va « rebondir » sur le dioptre et repartir dans le milieu 1 (comme un miroir) : c’est ce qu’on appelle le rayon réfléchi (le phénomène est appelé réflexion)
– soit le rayon va traverser le dioptre mais il sera dévié : c’est ce qu’on appelle le rayon réfracté (le phénomène est appelé réfraction) :
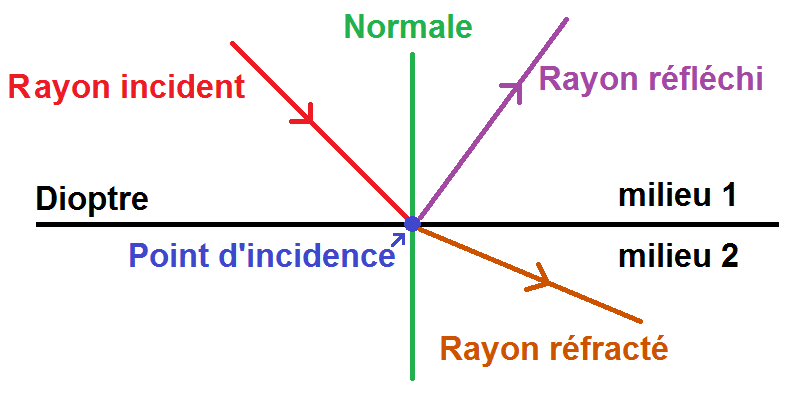
Il faut maintenant rajouter les angles correspondants à chaque rayon : l’angle d’incidence, l’angle de réflexion et l’angle de réfraction.
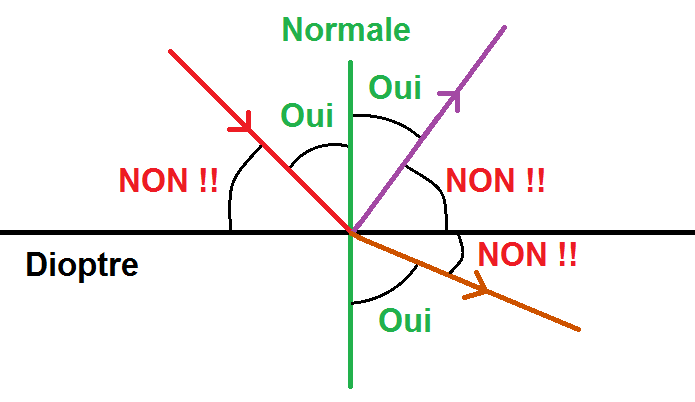
Ces angles sont toujours entre le rayon et la normale, PAS le dioptre !!!
—
Les angles d’incidence, de réflexion et de réfraction se situent entre la normale et le rayon, PAS entre le dioptre et le rayon.
C’est une erreur que les élèves font souvent…
—
Comme les angles d’incidence et de réflexion sont dans le milieu 1, ils sont souvent notés i1 et i’1, et comme l’angle de réfraction est dans le milieu 2 il est souvent noté i2 :
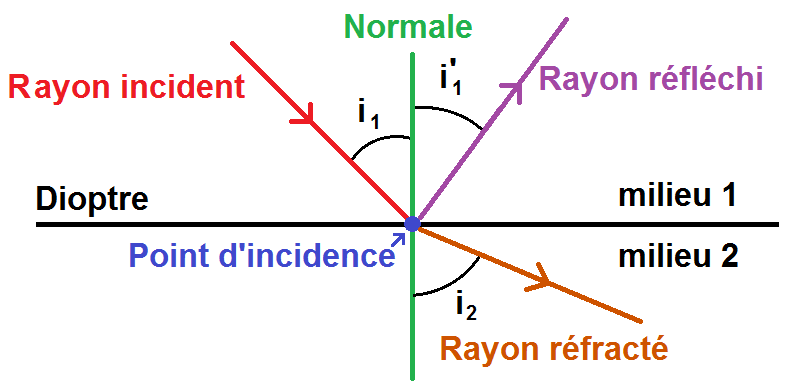
Pour illustrer le fait que les angles sont entre la normale et le rayon, et non entre le dioptre et le rayon :
On peut également parler du plan d’incidence, qui est tout simplement le plan du schéma, à savoir le plan qui contient à la fois le rayon incident et la normale (d’où le nom de plan d’incidence^^).
Nous ne le mettrons pas sur le schéma car il s’agit tout simplement du plan du schéma lui-même.
En revanche il est important d’avoir en tête la notion de plan d’incidence car elle sera utilisée dans la 1ère loi de Descartes.
Enfin, dernière chose que l’on peut rajouter sur le schéma (promis après il n’y a plus rien  ) : l’indice de réfraction des milieux.
) : l’indice de réfraction des milieux.
Tu dois savoir que dans chaque milieu (air, eau, verre, etc…) la vitesse de la lumière n’est pas la même. La vitesse est aussi appelée célérité.
Dans le vide, elle est notée c et vaut environ 3,00 x 108 m.s-1.
Dans l’eau elle est environ égale à 2,25 x 108 m.s-1, et dans le verre environ 2,00 x 108 m.s-1 par exemple.
On définit alors ce que l’on appelle l’indice de réfraction d’un milieu, noté n, défini par :
\(\displaystyle n = \frac{c}{v} \)
n est l’indice du milieu, sans unité puisque c’est une vitesse divisé par une vitesse
c est la célérité de la vitesse dans le vide (3,00 x 108 m.s-1)
v est la vitesse de la lumière dans le milieu considéré.
La valeur de c sera généralement donnée dans l’énoncé, elle sera parfois plus ou moins précise que 3,00 x 108 m.s-1.
Pour différencier les différents indices de réfraction, on mettra en petit le milieu en question : nvide, neau, nverre…
Ces 3 milieux (vide, eau et verre) sont les 3 milieux que tu rencontreras le plus en exercice.
Souvent, on considérera que l’air et le vide sont similaires (même si ce n’est pas vrai mais dans ce chapitre cela ne change pas grand chose).
Calculons alors leurs indices avec les valeurs données ci-dessus :
\(\textstyle n_{air} = \frac{c}{v_{air}} \)
\(\textstyle n_{air} = \frac{3,00 \times 10^8}{3,00 \times 10^8} \)
\(\textstyle n_{air} = 1 \)
—————
\(\textstyle n_{eau} = \frac{c}{v_{eau}} \)
\(\textstyle n_{eau} = \frac{3,00 \times 10^8}{2,25 \times 10^8} \)
\(\textstyle n_{eau} = 1,33 \)
—————
\(\textstyle n_{verre} = \frac{c}{v_{verre}} \)
\(\textstyle n_{verre} = \frac{3,00 \times 10^8}{2,00 \times 10^8} \)
\(\textstyle n_{verre} = 1,50 \)
Ces valeurs ne sont pas à connaître par cœur, elle seront données dans l’énoncé, ou alors on te donnera les vitesses et tu devras retrouver les indices comme on vient de le faire en appliquant les formules.
Dans tous les cas, n ≥ 1 puisque n = c/v, et que c est toujours supérieur à v puisque la lumière est la plus rapide dans le vide.
Ainsi le numérateur sera toujours plus grand que le dénominateur, donc n sera toujours supérieur ou égal à 1 !
\(\displaystyle n \ge 1 \)
Mais à quoi cela sert de savoir cela ?
Cela peut servir à vérifier que tu ne t’es pas trompé dans les calculs notamment. Cela peut aussi te servir dans un QCM où on te demande la valeur d’un indice de réfraction : tu peux déjà éliminer toutes les réponses qui sont plus petites que 1…
On peut désormais enfin terminer le schéma précédent en rajoutant les indices des milieux : celui du milieu 1 sera noté n1, et celui du milieu 2 sera noté… n2 comme tu l’auras deviné 
Le schéma est désormais complet, nous allons désormais pouvoir étudier les lois de Descartes.
L’énoncé de la première loi de Snell-Descartes est le suivant :
—
Le rayon réfracté et le rayon réfléchi appartiennent au plan d’incidence.
—
Autrement dit, tout se passe en 2D, dans le plan d’incidence !
Heureusement, car en 3D cela serait plus compliqué à dessiner…
Cela paraît logique mais la première loi de Descartes nous permet de l’affirmer.
Cette loi n’a pas beaucoup d’intérêt dans les exercices car elle ne donne aucun calcul, ce pourquoi il faut seulement retenir son énoncé qui pourra t’être demandé en question de cours.
Un autre énoncé, qui consiste à remplacer « plan d’incidence » par sa définition peut également être appris :
« Le rayon réfracté et le rayon réfléchi appartiennent au même plan que le rayon incident et la normale. »
Passons à la deuxième loi de Descartes.
La deuxième loi de Descartes concerne le rayon réfléchi, tandis que la 3ème loi de Descartes concerne le rayon réfracté.
—
Tu trouveras parfois le fait que la 2ème loi de Descartes concerne le rayon réfracté… et qu’il n’y a pas de 3ème loi de Descartes… 
C’est un peu bizarre mais retiens plutôt ce qui est présenté ici !
—
La deuxième loi de Snell-Descartes concerne donc le rayon réfléchi.
Cette loi nous dit tout simplement que le rayon réfléchi est égal au rayon incident !
\(\displaystyle i’_1 = i_1 \)
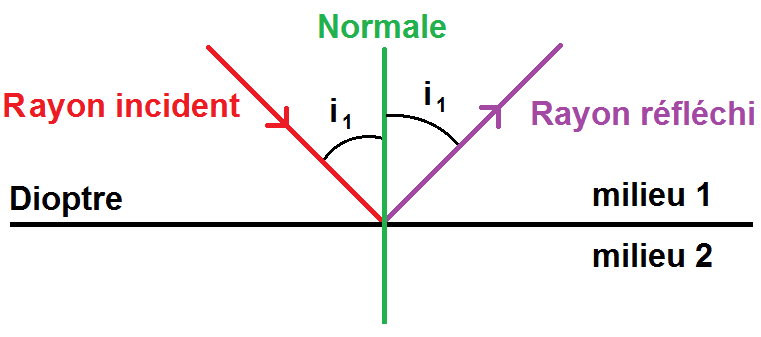
Cela paraît plutôt logique car le dioptre agit à ce moment-là comme un miroir, il renvoie donc la rayon lumineux symétriquement par rapport à la normale.
Cette 2ème loi de Descartes est très simple et ne permet pas non plus de faire beaucoup de calculs, il s’agit plus d’une propriété que d’une véritable formule.
La 3ème loi en revanche va nous permettre de faire des calculs mathématiques !
La 3ème loi de Snell-Descartes concerne, comme on l’a dit précédemment, le rayon réfracté. C’est pour cela qu’elle est aussi appelée loi de la réfraction.
On rappelle que l’on note i1 le rayon incident et i2 le rayon réfracté, n1 et n2 les indices des milieux 1 et 2.
On a alors la relation suivante, qui constitue la 3ème loi de Descartes :
\(\displaystyle n_1 sin(i_1) = n_2 sin(i_2) \)
Avec un schéma c’est encore mieux :
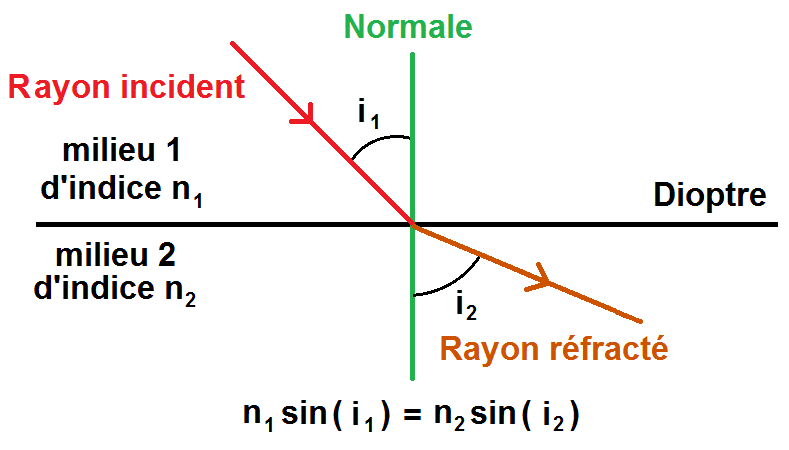
A partir de cette relation, on isole ce que l’on cherche.
Si on cherche n1 ou n2, c’est simple :
\(\textstyle n_1 = \frac{n_2 \, sin(i_2)}{sin(i_1)} \)
\(\textstyle n_2 = \frac{n_1 \, sin(i_1)}{sin(i_2)} \)
Si on cherche i1 ou i2 en revanche, il faut faire deux étapes : isoler le sinus, puis faire arcsin (aussi noté sin-1), la fonction réciproque de sinus :
\(\textstyle sin(i_1) = \frac{n_2 \, sin(i_2)}{n_1} \)
\(\textstyle i_1 = arcsin(\frac{n_2 \, sin(i_2)}{n_1}) \)
Et pour i2 :
\(\textstyle sin(i_2) = \frac{n_1 \, sin(i_1)}{n_2} \)
\(\textstyle i_2 = sin^{-1}(\frac{n_1 \, sin(i_1)}{n_2}) \)
(arcsin et sin-1 signifient la même chose)
Il suffit alors de remplacer avec les valeurs données dans l’énoncé.
Attention à bien mettre ta calculatrice en degrés et non en radians, dans ce type d’exercices les angles sont presque toujours donnés en degrés 
—
ATTENTION cependant !! La formule n1 sin(i1) = n2 sin(i2) doit être adaptée avec les données de l’énoncé.
Les indices ne seront pas forcément notés n1 et n2 mais nair et nverre par exemple.
De même les angles pourront être notés α et β par exemple.
—
Sur la schéma ci-dessous, la 3ème loi de Descartes s’écrira :
nair sin(α) = neau sin(β)
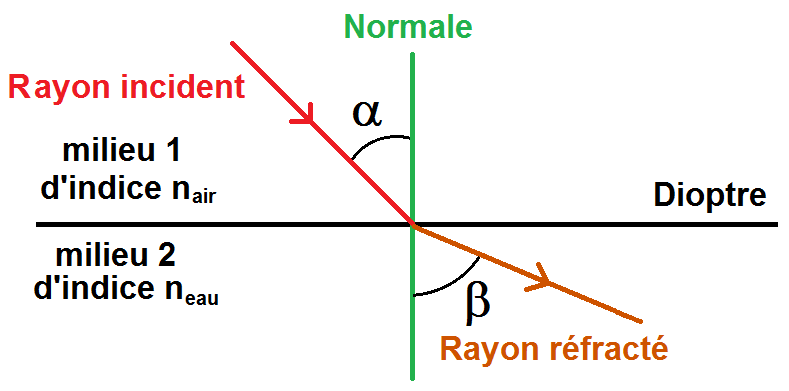
Sur les schémas précédents, on voit que le rayon réfracté est dévié par rapport à i1 (c’est le principe de la réfraction).
On a dessiné i2 > i1 sur les schémas, si bien que le rayon réfracté s’éloigne toujours de la normale par rapport à i1, mais ce n’est pas toujours le cas !
Comment savoir si le rayon réfracté va se rapprocher ou s’éloigner de la normale ?
Tout dépend des indices de réfraction !
La 3ème loi de Descartes peut s’écrire :
\(\textstyle \frac{n_1}{n_2} = \frac{sin(i_2)}{sin(i_1)} \)
– Si n1 > n2 :
\(\textstyle \frac{n_1}{n_2} \gt 1 \)
d’où :
\(\textstyle \frac{sin(i_2)}{sin(i_1)} \gt 1 \)
donc
\(\textstyle sin(i_2) \gt sin(i_1) \)
Ainsi
\(\textstyle i_2 \gt i_1 \)
(car la fonction sinus est croissante)
La rayon va alors s’éloigner de la normale.
– Si n1 < n2 : en faisant le même raisonnement, on trouverait i1 > i2 : le rayon va cette fois-ci se rapprocher de la normale.
—
Si n2 < n1, alors i2 > i1 : la rayon va s’éloigner de la normale.
Si n2 > n1, alors i2 < i1 : la rayon va se rapprocher de la normale.
—
—
On définit alors ce que l’on appelle la réfringence d’un milieu.
Plus l’indice de réfraction n d’un milieu est grand, plus il sera réfringent.
—
Par exemple : neau = 1,33 et nverre = 1,5, nverre > neau donc le verre est plus réfringent que l’eau.
Plus n est grand plus le rayon sera dévié : la réfringence d’un milieu est donc sa capacité à réfracter la lumière.
Tu sais désormais presque tout sur les lois de Descartes.
Presque ?? Oui, il reste une dernière chose à voir avant de passer aux exercices 
On a vu ci-dessus que l’angle de réfraction i2 est défini par :
\(\textstyle i_2 = arcsin(\frac{n_1 \, sin(i_1)}{n_2}) \)
Le problème est que la fonction arcsin est définie sur [-1 ; 1].
Ainsi arcsin(1,2) n’existe pas par exemple (tu peux tester avec ta calculatrice, elle te mettra un message d’erreur).
Ce qui est dans le arcsin doit donc être plus petit que 1 :
\(\textstyle \frac{n_1 \, sin(i_1)}{n_2} \, < \, 1 \)
n1 et n2 étant généralement des constantes, onva isoler i1 :
\(\textstyle sin(i_1) < \, \frac{n_2}{n_1} \)
\(\textstyle i_1 < arcsin(\frac{n_2}{n_1}) \)
Ce arcsin(n2/n1) constitue alors la valeur limite de l’angle d’incidence pour que i2 existe, c’est-à-dire pour qu’il y ait réfraction.
Mais on a dit précédemment que arcsin était définit sur [-1;1], donc il faut n2/n1 < 1 puisque l'on a arcsin(n2/n1) !
Il y a donc une condition à respecter : n2 < n1 : le milieu 2 doit être moins réfringent que le milieu 1.
Ceci est logique car si n2 < n1, on a vu que i2 > i1 : le rayon réfracté s’éloigne de la normale.
Mais pour une certaine valeur de i1, il va tellement s’éloigner qu’il sera confondu avec le dioptre : il n’y aura plus de réfraction !
Sur les trois schémas ci-dessous, i1 est de plus en plus grand, i2 augmente également, jusqu’à ce que i1 = ilim et alors il n’y a plus de rayon réfracté :
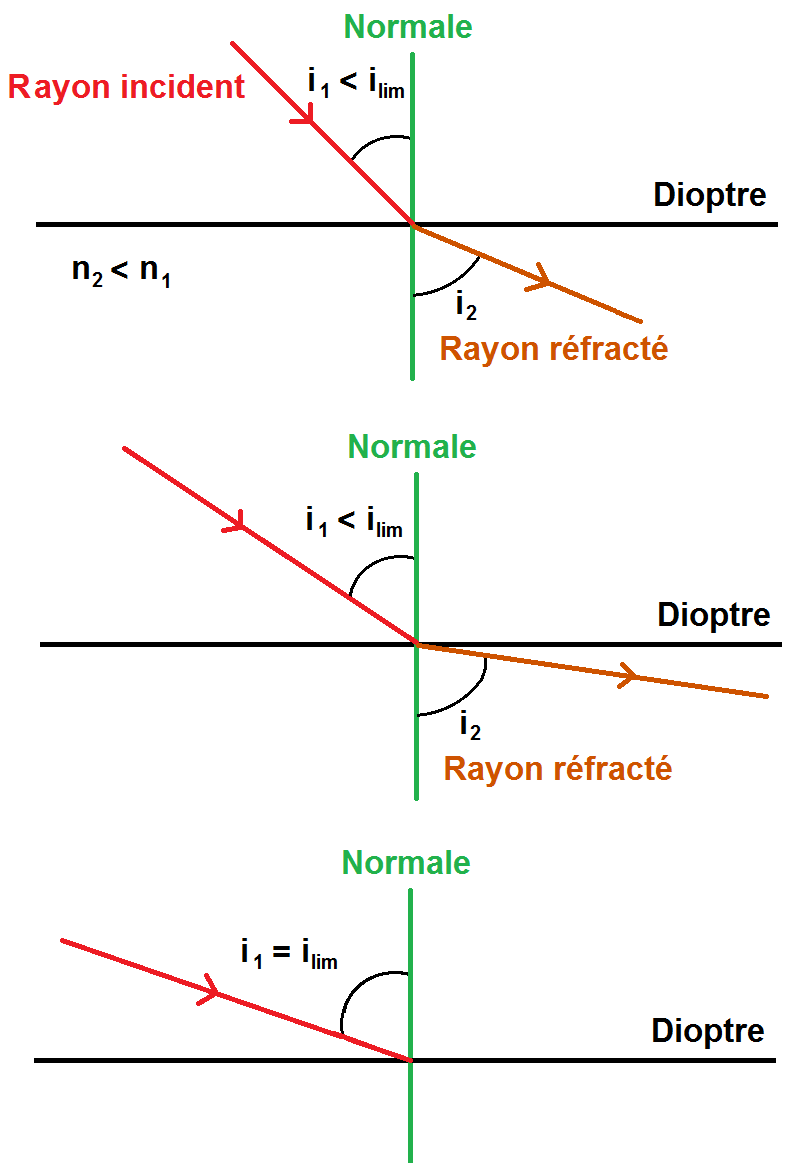
En revanche si n2 > n1 le rayon réfracté va au contraire se rapprocher de la normale et on aura donc toujours un rayon réfracté, donc jamais de réflexion totale.
Mais pourquoi parle-t-on de réflexion totale ??
Tout simplement parce que quand le rayon incident arrive sur le dioptre, il y a une partie de l’onde qui est réfléchie et l’autre partie qui est réfractée.
Mais quand i1 = ilim, il n’y a plus de rayon réfracté, l’onde est donc entièrement réfléchie, d’où le terme de réflexion totale !
—
Pour résumer : si n2 > n1, il n’y aura jamais de réflexion totale.
Si n2 < n1, il existe une valeur limite de i1 appelée ilim au-delà de laquelle il n’y a plus de réfraction : c’est la réflexion totale, l’onde incidente est entièrement réfléchie.
Cette valeur limite est définie par :
\(\textstyle i_{lim} = arcsin(\frac{n_2}{n_1}) \)
—
La réflexion totale est utile dans la fibre optique par exemple pour transmettre des ondes sans perte, nous étudierons cela dans les exercices.
Dernière chose avant de passer aux exercices : il ne faut pas confondre la réflexion totale avec un cas particulier : quand le rayon incident arrive perpendiculairement au dioptre.
Cela signifie que i1 = 0 (le rayon incident est confondu avec la normale).
Or on a vu que :
\(\textstyle i_2 = arcsin(\frac{n_1 \, sin(i_1)}{n_2}) \)
Si on remplace i1 par 0, cela donne sin(0) = 0
On a donc :
\(\textstyle i_2 = arcsin(\frac{n_1 \times 0}{n_2}) \)
\(\textstyle i_2 = arcsin(0) \)
\(\textstyle i_2 = 0 \)
Ainsi le rayon réfracté est confondu avec la normale, comme le rayon incident : le rayon n’est pas dévié.
—
Ainsi, si le rayon arrive perpendiculairement au dioptre, il ne sera pas dévié : c’est d’ailleurs le seul cas où il n’est pas dévié.
—
Maintenant que tu sais tout sur la loi de Descartes nous allons pouvoir passer aux exercices.
Tu trouveras tous les exercices sur les lois de Descartes sur cette page !
Retour au sommaireHaut de la page



Vraiment le document a été bien élaboré de toutes pièces, je vous le recommande de consulter ce document pour ne plus avoir de problème en optique géométrique merci !!!
Vraiment le document a été bien élaboré et c’est détaillé de toutes pièces, je vous conseil de consulter ce document pour ne plus avoir de problème au niveau de l’option géométrique merci !!!
Vraiment je suis très ravis de voir ce cours important, mes grands remerciements.
Merci , vous m’avez vraiment aidé à comprendre cette leçon,
C’est un cours vraiment important et en détai.Il m’a beaucoup aidé. Merci
Merci beaucoup. Je suis AESH en lycée et votre cours va nous être très utile à mes élèves et surtout à moi.
Un cours foormidable !! mercii bcp pour vos efforts !
merci beaucoup .Vous m avez aidé énormément et grâce à vous j ai compris cette leçon.