Sommaire
Introduction
Principe général : vocabulaire
Tracé des rayons lumineux
Relation de conjugaison
Grandissement
Modélisation de l’œil avec une lentille
Plan focal objet et plan focal image
Lentilles divergentes
Exercices
Dans ce chapitre, nous allons étudier les lentilles minces convergentes, ainsi que le fonctionnement de l’œil qui, comme on va le voir, peut s’apparenter à celui d’une lentille.
Dans tout le chapitre, les longueurs seront des longueurs algébriques, c’est-à-dire que si elle est dirigée vers la droite, elle sera positive, mais si elle est vers la gauche, elle sera négative.
Une longueur négative ?? 
Oui, cela peut paraître bizarre, c’est pour cela qu’une telle longueur s’appelle longueur algébrique, elle est notée avec une barre au-dessus. Cette barre sera parfois omise dans la suite du cours pour plus de facilité.
Exemple :
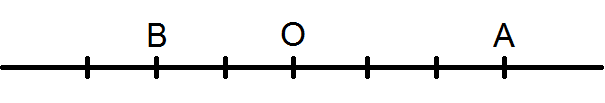
OA est dirigée vers la droite, elle est donc positive, mais OB vers la gauche et donc négative :
\(\textstyle \overline{OA} = 3 \)
\(\textstyle \overline{OB} = -2 \)
De même, BA est dirigée vers la droite, elle est donc positive, mais AB vers la gauche et donc négative :
\(\textstyle \overline{BA} = 5 \)
\(\textstyle \overline{AB} = -5 \)
Parfois pour simplifier au lycée, on ne prend pas en compte le fait que les distances soient algébriques, ce qui limite le nombre de formules et d’exercices possibles, donc nous ne ferons pas cette simplification.
Pour compenser ce problème, il est possible que tu utilises des axes x et y au lycée, ce qui permettra d’avoir des valeurs négatives. Les différentes formules que nous verrons seront donc exprimées avec les mesures algébriques et avec les coordonnées x et y afin que tu voies les deux méthodes.
Dans tout le chapitre, toutes les distances seront en mètres donc nous ne le mentionnerons pas à chaque fois.
Ces précisions étant faites, nous allons pouvoir commencer le chapitre à proprement parler.
Les lentilles minces que nous allons étudier sont dites convergentes par opposition à celles dites divergentes. Nous en dirons quelques mots en fin de chapitre mais ce n’est pas au programme du lycée.
Les lentilles convergentes sont convexes, tandis que les divergentes sont concaves :
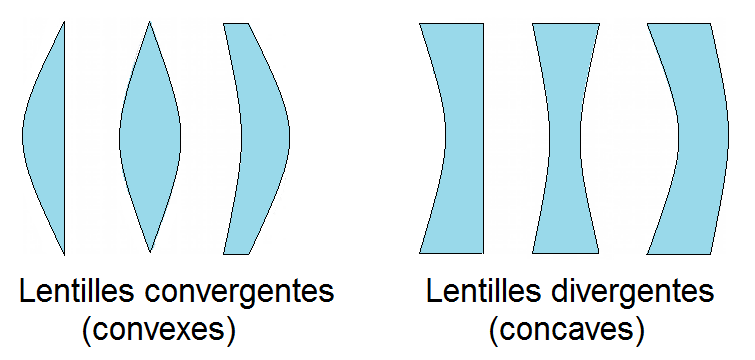
Dans la vie de tous les jours, ces lentilles minces sont par exemple des verres de lunettes, ou des lentilles de contact (d’où le terme de lentilles !).
Dans les exercices, nous allons bien sûr schématiser les lentilles, et ce de la manière suivante :
Les flèches sont très importantes, car nous verrons que pour une lentille divergente les flèches sont dans l’autre sens pour faire la différence.
A ce schéma nous allons rajouter le centre de la lentille, appelé centre optique, noté O, ainsi qu’une droite imaginaire appelée axe optique, perpendiculaire à la lentille et passant par O :
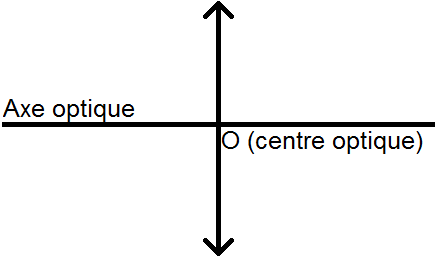
Cet axe correspond à l’axe x dont nous avons parlé dans l’énoncé, et O au centre du repère. La lentille constitue l’axe y :
Dans toute la suite nous ne mettrons pas les axes, ils seront sous-entendus.
Des rayons lumineux vont arriver par la gauche et ressortir à droite de la lentille en étant déviés (notamment à cause de la réfraction). On considère donc que la lumière se propage de la gauche vers la droite : c’est une convention, on pourrait faire l’inverse.
Ces rayons proviennent d’un objet, situé donc à gauche de la lentille, et l’image de cet objet va se former à droite de la lentille (sauf exception que nous verrons).
La convention est de noter avec ‘ les images, par exemple A’ est l’image de A, B’ est l’image de B, C’ est l’image de C etc…
Un objet AB aura donc une image A’B’.
En gros, tout ce qui est ‘ concerne les images, tout ce qui n’est pas ‘ concerne les objets (sauf exception).
Nous allons alors pour terminer rajouter de part et d’autre de l’axe optique deux points imaginaires, F et F’, respectivement foyer objet et foyer image. Ils sont situés à égale distance de O, F étant à gauche et F’ à droite (puisque les images seront à droite) :
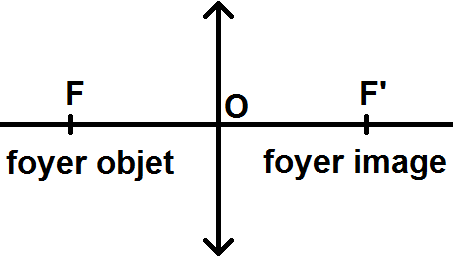
D’après ce que l’on a dit sur les distances algébriques en introduction, et comme F et F’ sont situés à égale distance de O, on a :
\(\textstyle \overline{OF’} \gt 0 \)
\(\textstyle \overline{OF} \lt 0 \)
\(\textstyle \overline{OF’} = -\overline{OF} \)
On définit alors la distance focale notée f’ comme étant la distance entre le centre et un foyer. La distance focale étant positive, on la définira donc comme OF’ plutôt que comme OF :
\(\textstyle f’ = \overline{OF’} \)
Avec les coordonnées :
\(\textstyle f’ = x_{f’} \)
En réalité, on définit la distance focale image f’ comme étant OF’ (donc positive), et la distance focale objet f comme étant OF (donc négative) :
\(\displaystyle f’ = \overline{OF’} \gt 0 \)
p style= »text-align:center »>distance focale image
\(\displaystyle f = \overline{OF} \lt 0 \)
p style= »text-align:center »>distance focale objet
\(\displaystyle f’ = -f \)
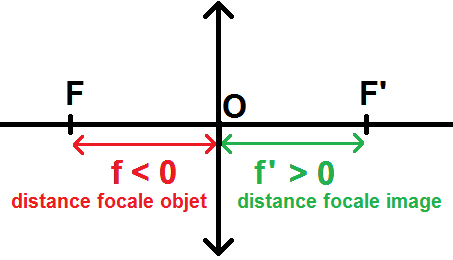
Quand on parle de distance focale (sans préciser objet ou image), on sous-entend la distance focale image car c’est elle qui est positive. Parfois au lycée on simplifie en prenant la valeur absolue comme ça aucun problème de signe.
Il arrive même de parler simplement de focale (en photographie par exemple), sous-entendu distance focale image.
—
ATTENTION à ne pas confondre foyer image et foyer objet qui sont des points (F et F’ sur le schéma), avec les distances focales f et f’ qui sont des distances.
—
On parle parfois de vergence, définie comme l’inverse de la distance focale. Elle est utilisée pour les lunettes notamment (on parle de la vergence d’un verre de lunette plutôt que de sa distance focale).
La vergence notée V, est donc :
\(\displaystyle V = \frac{1}{f’} \)
Remarque : on prend f’ plutôt que f pour que V soit positive.
V est donc en m-1 puisque f’ est en mètres, mais on parle aussi en dioptrie noté δ (delta).
V peut ainsi être exprimée en δ ou en m-1 (ce qui revient au même : 1 δ = 1 m-1).
Maintenant que le schéma a été défini et le vocabulaire précisé, nous allons pouvoir passer à la partie la plus importante : le tracé des rayons lumineux.
De manière générale, un objet réfléchissant des ondes dans toutes les directions, plusieurs rayons lumineux vont provenir d’un même point.
Mais 3 rayons particuliers vont nous intéresser, car il existe des règles pour savoir comment ils vont être déviés.
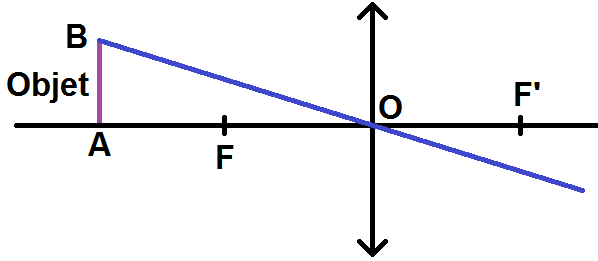
On considère donc un objet AB, A étant sur l’axe optique.
On cherche son image A’B’ : pour cela on va chercher l’image B’, et on en déduira la position de A’ (qui sera la projection sur l’axe optique de B’).
En effet, A étant sur l’axe optique, A’ sera nécessairement sur cet axe également.
Les 3 rayons intéressants sont les suivants :
1) le rayon qui passe par B et par O.
La règle est la suivante :
—
Tout rayon passant par O n’est pas dévié.
—
Graphiquement, cela donne :
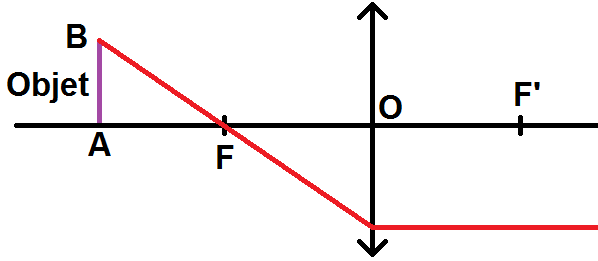
2) le rayon qui passe par B et par F.
La règle est la suivante :
—
Tout rayon passant par F ressort parallèlement à l’axe optique (donc horizontal sur le schéma).
—
Graphiquement, cela donne :
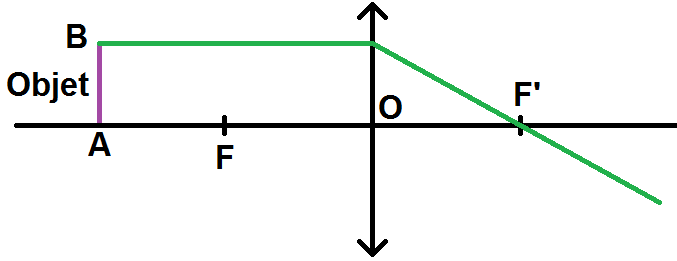
3) le rayon qui passe par B et parallèle à l’axe optique.
La règle est la suivante :
—
Tout rayon parallèle à l’axe optique (donc horizontal sur le schéma) passe par F’.
—
Graphiquement, cela donne :
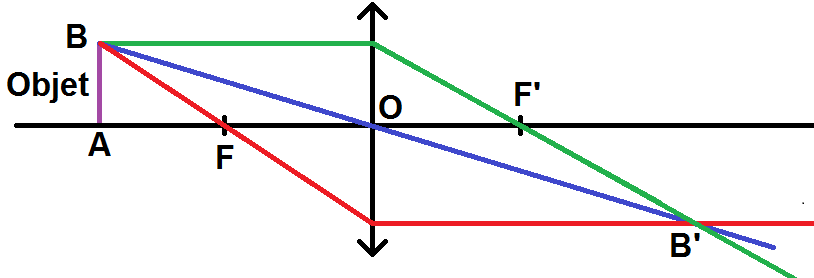
Avec ces 3 règles, on peut donc tracer 3 rayons passant par B : ces rayons vont se couper en un point qui sera B’ :
On en déduit alors la position de A’ :
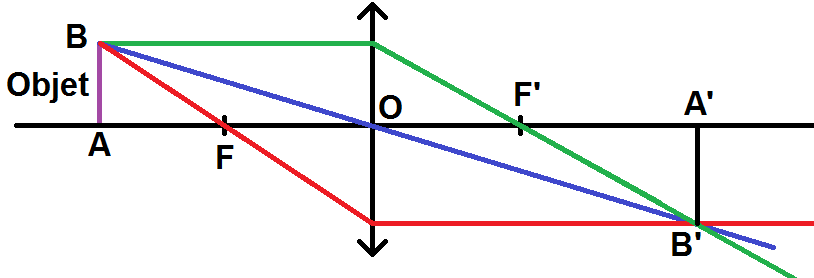
Remarque : évidemment 2 rayons suffisent pour trouver B’, mais rien ne t’empêche de faire le 3ème pour vérifier que tu ne t’es pas trompé : les trois rayons doivent être concourants.
Afin d’observer l’image, il faut mettre un écran au niveau de l’image A’B’ ou mettre son œil (c’est alors l’œil qui joue le rôle d’écran, et en particulier la rétine, nous en reparlerons plus loin dans le cours).
Remarque : d’après les schémas ci-dessus, on a :
\(\textstyle \overline{OA} = x_A \)
\(\textstyle \overline{OA’} = x_{A’} \)
\(\textstyle \overline{AB} = y_B \)
\(\textstyle \overline{A’B’} = y_{B’} \)
Nous utiliserons cela par la suite.
Cas particulier pour le tracé des rayons : si AB est situé entre F et O, les trois rayons ne seront apparemment pas concourants :
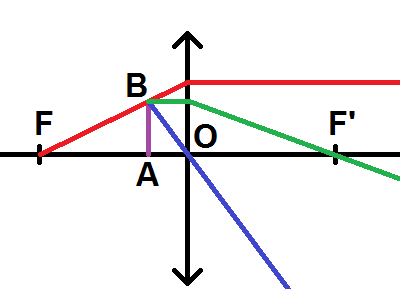
Il faut dans ce cas les prolonger virtuellement à gauche de la lentille (donc en pointillés) pour trouver le point où ils se coupent, et qui correspond à B’ :
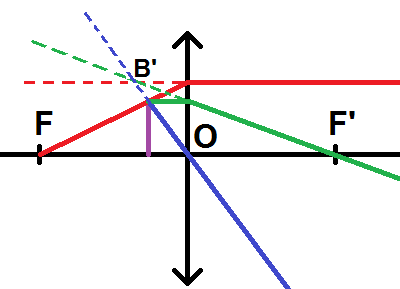
Attention, il faut bien prolonger les rayons en pointillés car ils ne vont pas réellement de ce côté mais virtuellement : c’est ce que l’on appelle une image virtuelle !
Dans ce cas, l’image est située à gauche de la lentille et non à droite : on a donc OA’ < 0 soit xA’ < 0.
On a alors la règle suivante :
—
Si xA’ > 0, l’image est réelle, si xA’ < 0, l’image est virtuelle.
Si OA’ > 0, l’image est réelle, si OA’ < 0, l’image est virtuelle.
—
L’image virtuelle correspond au même principe que lorsque tu te regardes dans un miroir, tu as l’impression d’être de l’autre côté mais en réalité il n’y a rien, c’est juste que les rayons convergent derrière le miroir, d’où l’illusion.
Dans les exercices, il s’agira de tracer les rayons pour trouver la position d’une image à partir de celle d’un objet, ou à l’inverse trouver la position d’un objet connaissant celle de l’image. On peut très bien en effet partir de B’ et faire le raisonnement inverse pour trouver B.
Le problème du tracé des rayons lumineux est évidemment la précision, comme tout tracé graphique.
Mais on peut trouver par le calcul la position de l’objet et de l’image grâce à une formule appelée relation de conjugaison.
Cette relation est la suivante :
\(\displaystyle \frac{1}{\overline{OA’}} – \frac{1}{\overline{OA}} = \frac{1}{f’} \)
Avec les coordonnées :
\(\displaystyle \frac{1}{x_{A’}} – \frac{1}{x_{A}} = \frac{1}{f’} \)
A partir de cette formule, on isole ce que l’on cherche avant de remplacer par les valeurs.
Si on te donne OA et f’ dans l’énoncé, tu pourras en déduire OA’.
Si on te donne OA’ et f’ dans l’énoncé, tu pourras en déduire OA.
Si on te donne OA et OA’ dans l’énoncé, tu pourras en déduire f’.
Exemple :
On dispose d’une lentille de distance focale f ‘ = 15 cm.
Calculer la position de l’image d’un objet situé à 20 cm de la lentille.
Réponse : tout d’abord, l’objet étant situé à 20 cm de la lentille, xA = -20 cm (attention au signe !!).
On cherche xA’, isolons-le dans la formule :
\(\textstyle \frac{1}{x_{A’}} – \frac{1}{x_{A}} = \frac{1}{f’} \)
\(\textstyle \frac{1}{x_{A’}} = \frac{1}{x_{A}} + \frac{1}{f’} \)
Attention ici à ne surtout pas dire xA’ = xA + f’, on n’a pas le droit d’inverser à cause de la somme !!
Pour inverser, il faut d’abord mettre au même dénominateur :
\(\textstyle \frac{1}{x_{A’}} = \frac{f’}{x_Af’} + \frac{x_A}{x_Af’} \)
\(\textstyle \frac{1}{x_{A’}} = \frac{f’ + x_A}{x_Af’} \)
\(\textstyle x_{A’} = \frac{x_Af’}{f’ + x_A} \)
On peut tout laisser en cm car les conversions vont s’annuler, on aura alors le résultat en cm :
\(\textstyle x_{A’} = \frac{-20 \times 15}{15 – 20} \)
\(\textstyle x_{A’} = 60 cm \)
L’image sera donc située à 60 cm de la lentille, et l’image sera réelle car xA’ > 0.
Comme tu le vois c’est un calcul plutôt simple mais il faut inverser correctement les fractions !
Comme tu as pu le constater sur les schémas précédents, l’image n’a pas forcément la même taille que l’objet, et elle parfois renversée (dirigée vers le bas alors que l’objet est vers le haut).
Quand l’objet et l’image sont dans le même sens, on dit que l’image est droite, sinon on dit qu’elle est renversée.
Quand l’image est plus grande que l’objet, on dit qu’elle est agrandie, sinon on dit qu’elle est réduite.
On définit alors le grandissement, noté G ou γ (gamma), sans unité, défini de la manière suivante :
\(\displaystyle \gamma = \frac{\overline{A’B’}}{\overline{AB}} = \frac{\overline{OA’}}{\overline{OA}} \)
Avec les coordonnées :
\(\displaystyle \gamma = \frac{y_{B’}}{y_B} = \frac{x_{A’}}{x_A} \)
Le grandissement peut donc s’exprimer de deux manières différentes : avec la taille de l’objet et de l’image (AB et A’B’) ou avec la position de l’objet et de l’image (OA et OA’).
Nous ferons un peu plus loin la démonstration de cette égalité.
Là encore ce sont des longueurs algébriques : positives si dirigées vers le haut, négatives si dirigées ver le bas.
Sur le schéma ci-contre, AB > 0 et A’B’ < 0, OA’ > 0 et OA < 0, :

Ainsi, plusieurs cas se présentent :
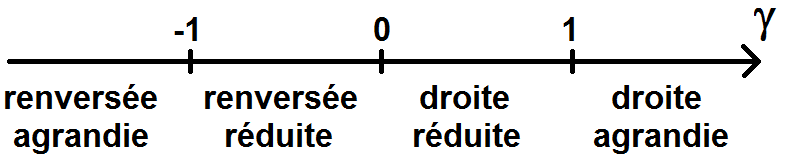
Si γ > 1 : cela signifie que l’image est dans le même sens que l’objet et plus grande que l’objet ;
Si γ < -1 : cela signifie que l’image est renversée par rapport à l’objet et plus grande que l’objet ;
Si 0 < γ < 1 : cela signifie que l’image est dans le même sens que l’objet et plus petite que l’objet ;
Si -1 < γ < 0 : cela signifie que l’image est renversée par rapport à l’objet et plus petite que l’objet ;
On peut également uniquement regarder la valeur absolue, ce qui donnera une idée de la taille de l’objet (mais pas de son sens) :
Si |γ| > 1 : l’image est plus grande que l’objet ;
Si |γ| < 1 : l’image est plus petite que l’objet ;
Si on regarde uniquement le signe, on aura des informations sur le sens de l’objet (mais pas sa taille) :
Si γ > 0 : l’image est dans le même sens que l’objet ;
Si γ < 0 : l’image est renversée par rapport à l’objet ;
On peut récapituler de la manière suivante :
\(\displaystyle \gamma \lt -1 \, :\, \)
\(\displaystyle image\, renversée\, agrandie \)
\(\displaystyle -1 \lt \gamma \lt 0 \,:\, \)
\(\displaystyle image \,renversée \,réduite \)
\(\displaystyle 0 \lt \gamma \lt 1 \,: \)
\(\displaystyle image\, droite\, réduite \)
\(\displaystyle \gamma \gt 1 \,:\ \)
\(\displaystyle image\, droite\, agrandie \)
Démontrons l’égalité du grandissement vue précédemment.
On a le schéma suivant (le rayon passant par F sert juste à la construction, mais pas à la démonstration) :
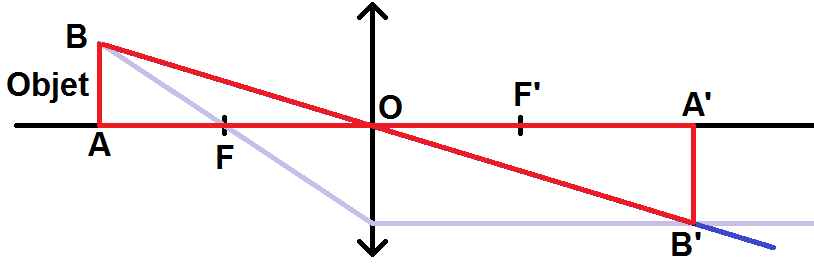
AB et A’B’ étant parallèles, on peut appliquer le théorème de Thalès dans la figure rouge :
\(\textstyle \frac{A’B’}{AB} = \frac{OA’}{OA} = \frac{OB’}{OB} \)
La dernière fraction n’a aucun intérêt, mais si on regarde les deux premières fractions, elles correspondent au grandissement !
Ici les longueurs ne sont pas prises de manière algébrique car le théorème de Thalès ne précise rien là-dessus mais on pourrait montrer que cette égalité est correcte avec les longueurs algébriques.
Le fonctionnement de l’œil humain est similaire à celui d’une lentille.
Voyons tout d’abord le vocabulaire lié à l’œil et son schéma :
L’iris agit comme un diaphragme qui peut plus ou moins s’ouvrir afin de laisser entrer plus ou moins de lumière : s’il y a beaucoup de lumière, il va se fermer afin de ne pas être ébloui, s’il y a peu de lumière il va au contraire s’ouvrir en grand pour capter le maximum de lumière. L’iris sera modélisé par un diaphragme.
A noter que l’iris est la partie colorée de l’œil.
L’ensemble des milieux transparents correspond à une lentille convergente (parfois tu verras que l’on considère uniquement le cristallin comme une lentille).
Enfin, la rétine correspond à un écran : c’est là que se forme l’image.
On peut ainsi modéliser l’œil par le schéma suivant :
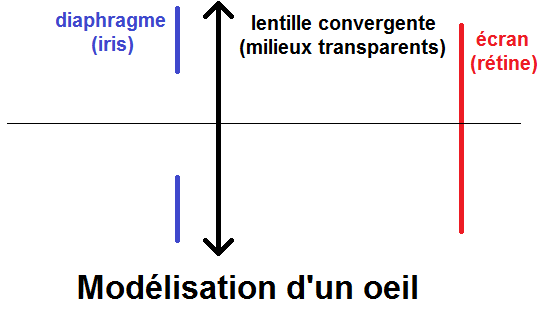
Remarque importante : l’image se formera à l’envers sur la rétine, c’est le cerveau qui remet l’image à l’endroit. L’image est acheminée au cerveau via le nerf optique, qui relie la rétine au cerveau.
La distance entre le cristallin et le rétine est fixe (environ 17 mm pour un œil humain) : la distance entre la lentille et l’écran est donc fixe. Cela signifie que la distance OA’ est toujours la même, mais OA n’est pas toujours la même (les objets que tu regardes ne sont pas tous à la même distance).
Comment fait l’œil humain pour que l’image d’un objet regardé soit toujours sur la rétine ?? 
—
Le cristallin va légèrement se déformer afin de changer sa distance focale f’, ce qui permet à l’image de toujours se former sur la rétine ! On dit alors que l’œil accommode.
—
Retiens bien ce principe de fonctionnement (déformation du cristallin pour modifier sa distance focale) car cela est souvent demandé en exercice !
Retiens bien également que la distance entre le cristallin et la rétine est fixe.
Il existe deux cas particuliers que nous allons étudier car ils peuvent être donnés en exercice.
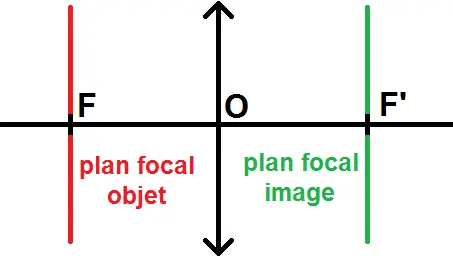
Avant cela, on va définir le plan focal objet et le plan focal image.
Le plan focal objet est un plan imaginaire perpendiculaire à l’axe optique et passant par le foyer objet F.
Le plan focal image est un plan imaginaire perpendiculaire à l’axe optique et passant par le foyer image F’.
Le 1er cas particulier est si un objet se trouve à l’infini. Quand on dit l’infini, on sous-entend assez loin sans qu’une valeur précise ne soit donnée. On peut se baser sur l’ordre de grandeur de la distance focale : si celle-ci est de 15 cm par exemple, on peut considérer que 100 m correspond à l’infini.
La règle est la suivante :
—
Si un objet se trouve à l’infini, son image se situe dans le plan focal image.
A’ est alors situé sur F’ : A’ = F’.
—
L’objet étant à l’infini, il est difficile de tracer les rayons lumineux comme précédemment. En réalité cela est possible (pas à l’échelle évidemment) mais ce n’est pas au programme du lycée donc nous n’en parlerons pas.
Le deuxième cas particulier correspond à l’inverse, à savoir si un objet se trouve dans le plan focal objet : son image est alors à l’infini.
—
Si un objet se trouve dans le plan focal objet, son image se situe à l’infini.
A est alors situé sur F.
—
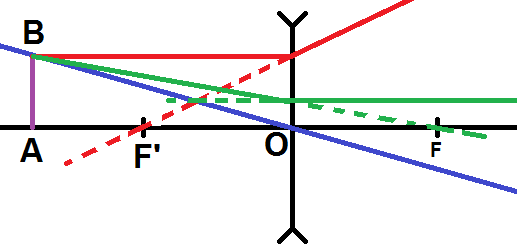
Traçons un exemple :
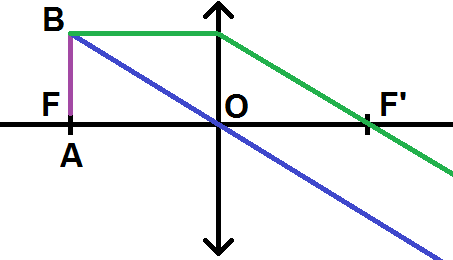
Comme tu le vois, ici on ne peut pas tracer le rayon passant par B et par F (ce rayon serait vertical).
Pour les deux autres rayons, on pourrait montrer qu’ils sont parallèles, donc ils ne vont pas se couper.
Mais alors, où est l’image ?? 
L’image est à l’infini !! On l’a dit précédemment, puisque l’objet est dans le plan focal objet.
Il s’agit en fait d’une propriété que l’on peut généraliser :
—
Les rayons passant par un point situé à l’infini sont parallèles.
Ce point peut appartenir à l’objet ou à l’image.
—
Là encore ce n’est pas vraiment au programme du lycée donc nous n’irons pas plus loin dans les détails.
Avant de passer aux exercices, voyons rapidement les lentilles divergentes.
Pour les lentilles divergentes, la différence avec les lentilles convergentes est l’inversion de F et F’ :
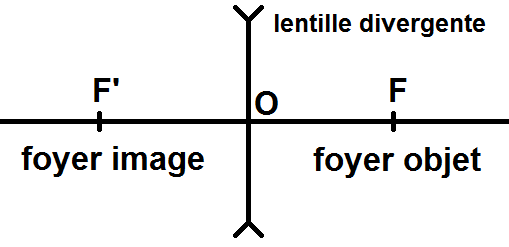
Au niveau de la notation, les flèches en haut et en bas de la lentille sont inversées pour faire la différence.
Le tracé des rayons est alors souvent virtuel car les rayons ne passent pas réellement pas F et F’ :
Nous n’irons pas plus loin dans l’étude des lentilles divergentes car ce n’est pas l’objet du chapitre, c’est juste pour que tu vois la différence 
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !
Sommaire des coursHaut de la page


