Sommaire
La poussée d’Archimède
La poussée d’Archimède : exercice 2
Loi de la statique des fluides
Loi de la statique des fluides : exo 2
La presse hydraulique
Le crève tonneau de Pascal
Pression en fonction de l’altitude
Soulèvement d’une calotte sphérique
Exercice de l’arrosoir
Pour accéder au cours sur la statique des fluides, clique ici !
On immerge un cube de côté a et de masse volumique ρ dans l’eau (de masse volumique ρeau).
1) A quelle condition l’objet remonte-t-il à la surface ?
2) Quelle sera alors la hauteur de la partie immergée ?
On considère maintenant 3 rondis de diamètre D et de longueur L placés dans l’eau avec une plaque de masse m par-dessus :

1) Quelle est la fraction F (en %) du volume immergé ?
2) Quelle est la masse maximale m’ de la plaque pour que l’ensemble ne coule pas ?
On considère un tube en U fermé à une extrémité. Il contient un gaz à la pression P inconnue (que l’on va déterminer), ainsi que deux liquides de masse volumique ρ1 et ρ2 connues.
On prendra un axe vertical ascendant, et on suppose connues les hauteurs zA, zB et zC des points A, B et C définis comme sur le schéma ci-dessous :
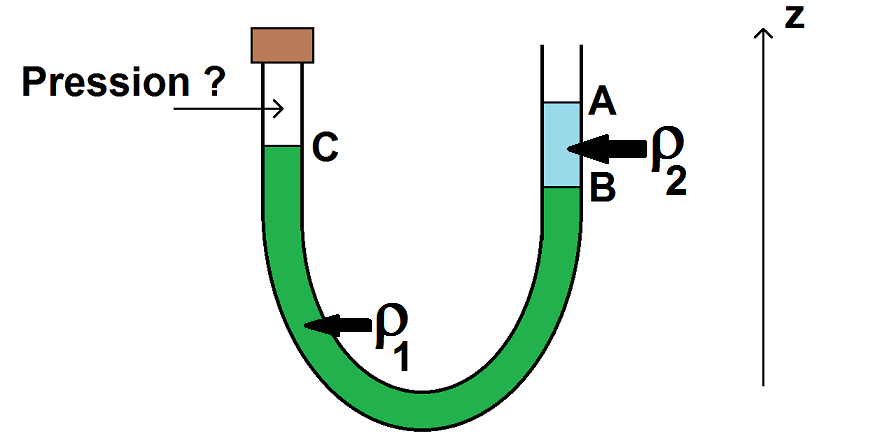
Le but est d’exprimer la pression P en fonction de zA, zB, zC, ρ1, ρ2, la constante g et la pression atmosphérique notée Patm.
On considère un récipient avec 2 tuyaux contenant de l’eau (de masse volumique ρe) et de l’huile (de masse volumique ρh) selon le schéma ci-dessous :
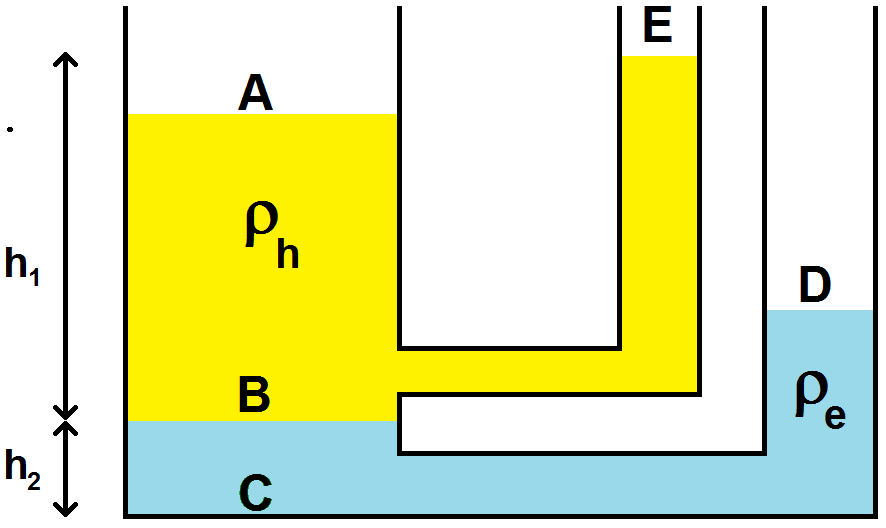
On suppose connues les différences de hauteur zE – zB = h1 et zB – zC = h2.
Le but de l’exercice est d’exprimer zD en fonction de h1, h2, ρh et ρe.
On considère un réservoir avec de l’eau avec un plateau de chaque côté, de surface S1 et S2 avec S1 < S2 selon le schéma suivant :
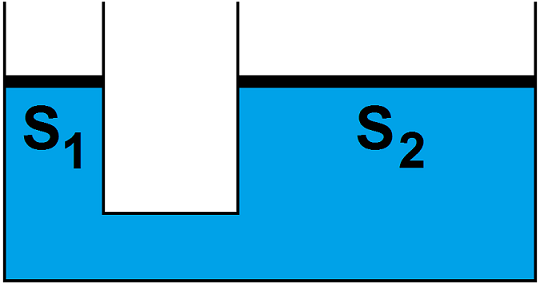
On applique une force F1 sur le plateau 1. Il y a alors une force F2 au niveau du plateau 2.
1) Donner la relation entre F1, F2, S1 et S2.
2) On met une masse M1 = 10 kg sur le plateau 1 et M2 = 90 kg sur le plateau 2. Donner la relation entre les rayons R1 et R2 des plateaux en supposant que les plateaux sont des disques.
3) Discuter de l’aspect énergétique de ce système.
On considère un tonneau de diamètre 65 cm et de hauteur 1 m rempli d’eau.
On perce le tonneau au centre du couvercle supérieur et on y met un tube de longueur h = 5,0 m et de diamètre 2 cm.
On remplit également d’eau ce tube.
1) Quelle est la surpression dans le tonneau due à ce tube rempli d’eau ?
2) Montrer que cela permet de faire exploser le tonneau.
3) Calculer la masse équivalente qu’il faudrait mettre sur le couvercle pour avoir la même surpression. Commenter.
On considère un axe vertical (Oz).
Déterminer la pression P(z) dans les cas suivants :
1) le fluide est incompressible
2) la masse volumique ρ dépend de z, et on considère l’air comme un gaz parfait isotherme
3) on considère que la température T(z) = T0 – az avec a > 0
On considère une calotte sphérique de rayon R, ouverte à son extrémité supérieure, remplie d’eau jusqu’au à la hauteur h.
La pression atmosphérique est notée P
Déterminer la hauteur h à partir de laquelle la calotte sphérique va se soulever.
On considère un arrosoir dans lequel on met de l’eau et de l’huile.
La hauteur d’eau et d’huile dans le corps principal est h, et celle d’eau dans le bec est z, ce qui correspond à une longueur L.
L’angle du bec avec l’horizontal est noté θ, et la pression atmosphérique P0.
La masse volumique de l’huile est ρh = 900 kg.m-3 et celle de l’eau est ρe = 1000 kg.m-3
On obtient le schéma suivant :
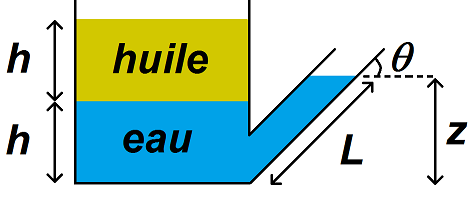
Exprimer θ en fonction de L, h, ρh et ρe.
Retour au coursHaut de la page



Brovoooo et merci infiniment
J(aime bien ces vidéos.
Bonne continuation Professeur