Loi d’Ohm : les résistances électriques

Sommaire

Introduction
Résistance et loi d’Ohm
Résistances en série
Résistances en parallèle
Ampèremètre et voltmètre
Exercices

Introduction
Nous parlerons dans ce chapitre de la loi d’ohm avec les résistances, il s’agit de ce que l’on voit en premier en électricité car les résistances sont les dipôles les plus simples à étudier.
Il est fortement conseillé (si ce n’est déjà fait) de lire le chapitre sur les bases de l’électricité car il s’agit d’un prérequis important pour n’importe quel chapitre d’électricité.

Résistance et loi d’Ohm

Une résistance électrique est un dipôle qui se branche dans un circuit.
Elle est caractérisée par une valeur appelée résistance notée R.
Elle est exprimée en Ohm, qui se note Ω (la lettre grecque oméga majuscule).
Par exemple R = 20 Ω ou R = 3,5 Ω.
Contrairement aux intensités et aux tensions, une résistance est toujours positive !
Elle est représentée par un rectangle de la manière suivante :

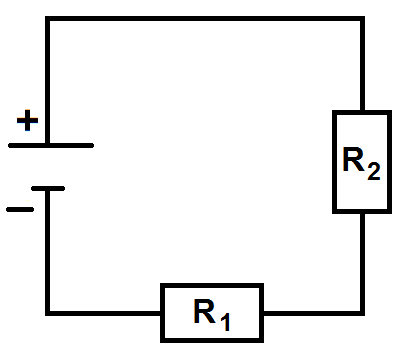
Ici comme il y a deux résistances elle ont été notées R₁ et R₂ mais tout dépend de l’énoncé.

Le courant qui traverse la résistance est le même avant et après l’avoir traversé puisque l’on est sur le même fil.
En revanche, le potentiel n’est pas le même avant et après : il y a donc une différence de potentiel et donc une tension.
Cette tension est parfois notée U_R pour que l’on comprenne que c’est la tension aux bornes de la résistance :

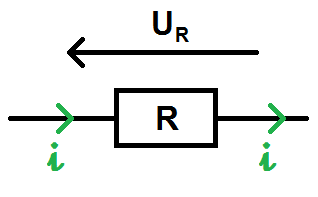
Cette tension est liée à la valeur R de la résistance et à l’intensité du courant par une formule que l’on appelle la loi d’ohm :

—
ATTENTION !! Cette formule est valable UNIQUEMENT pour les résistances, pas pour les bobines, les condensateurs, les générateurs ou n’importe quel autre dipôle.
—

Comme la tension aux bornes de la résistance est parfois notée U_R, on peut donc également avoir

Il s’agit de la même formule, le R en indice du U dans le U_R est uniquement là pour marquer le fait qu’il s’agisse de la tension aux bornes de la résistance, ce n’est PAS U × R…

Un point très important sur lequel il faut faire attention est le sens du U et du I.
En effet, d’après le schéma ci-dessus, on voit que U et I sont en sens inverse : c’est ce que l’on appelle la convention récepteur.
En effet, dans le circuit la résistance reçoit le courant qui passe à travers, ce n’est pas elle qui génère le courant, c’est le générateur !
Ainsi, à l’inverse de la convention récepteur où U et I sont en sens inverse, il existe une convention générateur où U et I sont dans le même sens !

—
Pour la convention récepteur, U et I sont en sens contraire.
Pour la convention générateur, U et I sont dans le même sens.
—

Ainsi, quand on a un générateur, on met U et I dans le même sens, si on a un récepteur (une résistance, une bobine etc…) on met U et I dans le sens inverse.
Tout cela est destiné à avoir des tensions et des intensités positives pour ne pas compliquer les calculs.
Si on ne respecte pas cette convention, l’une des deux valeurs (U ou I) sera négative. Ce n’est pas grave mais cela complique les calculs et augmente le nombre de chances de se tromper.

En effet, on a vu que U = RI.
R étant positif, U et I sont de même signe. Mais si on est en convention générateur pour la résistance (U et I dans le même sens), on vient de voir que l’un des deux est négatifs !!

Alors comment faire ??
Il suffit de mettre un signe – si l’on est en convention générateur

Ainsi la loi d’ohm peut s’écrire de deux manières suivant les cas :

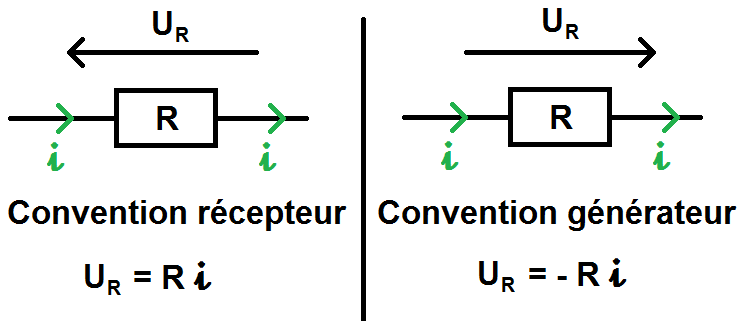
Si tu peux toi-même choisir l’orientation du I et du U de la résistance, fais en sorte qu’ils soient en convention récepteur (en sens inverse) afin de ne pas avoir de signe -. Si tu n’as pas le choix, il faut faire attention et bien vérifier dans quel convention on se trouve.

Résistances en série

Haut de page

Dans de nombreux exercices, il n’y a pas une mais des résistances dans le circuit électrique.
Suivant la disposition des résistances dans le circuit, il est possible de regrouper certaines résistances en une seule, appelée résistance équivalente.

Il y a alors deux cas possibles :
– soit les résistances sont en série, c’est-à-dire alignées sur un même fil ;
– soit les résistances sont en parallèle.

Dans l’exemple nous avons mis 3 résistances en série ou en parallèle, mais il peut n’y en avoir que deux comme il peut y en avoir beaucoup plus, il n’y a pas de limite !

Étudions les deux cas séparément.

Tout d’abord les résistances en série : reprenons le schéma ci-dessus et mettons l’intensité et les tensions :

On remarque tout d’abord que l’intensité est la même, puisque l’on est sur un même fil. Il pourrait y avoir encore plus de résistances cela ne changerait rien.
En revanche, les tensions U₁, U₂ et U₃ sont différentes.
En effet, d’après la loi d’ohm, on a :
U₁ = R₁i, U₂ = R₂i et U₃ = R₃i

Le i est le même mais les résistances R₁, R₂ et R₃ ne sont pas les mêmes, donc les tensions sont différentes.

L’intensité i a donc 3 expressions différentes :

Ainsi, on peut trouver U₁ par exemple en connaissant U₃, R₁ et R₃, même sans connaître le i.

Le plus important est que l’on peut regrouper les résistances en une résistance équivalente notée R_éq (elle peut très bien être notée différemment suivant l’énoncé).
Cette résistance équivalente est tout simplement égale à la somme des résistances regroupées :

(La double flèche indique, comme en maths, que les deux schémas sont équivalents)

Comme indiqué sur le schéma, la tension aux bornes de cette résistance équivalente est la somme des tensions des résistances regroupées.

—
Pour des résistances en série, la résistance équivalente est égale à la somme des résistances regroupées.
La tension équivalente est aussi égale à la somme des tensions regroupées.
—

On peut très bien regrouper uniquement certaines résistances et pas d’autres :

Ici on a uniquement regroupé R₁ et R₂ et on a laissé R₃, tout dépendra de l’énoncé !

A noter que l’ordre des résistances importe peu, on peut très bien inverser l’ordre des résistances en série :

Si l’intensité ne change évidemment pas, les tensions cependant correspondent toujours à leur résistance (R₁ avec U₁, R₂ avec U₂ etc…).

L’intérêt de regrouper des résistances est de diminuer le nombre de variables.
Dans l’exemple ci-dessus, au lieu d’avoir 3 résistances et 3 tensions, on n’a plus qu’une résistance et une seule tension, réduisant le nombre de variables.
Nous verrons dans les exercices des applications concrètes de ce principe.

Résistances en parallèle

Haut de page

Voyons maintenant ce qui se passe quand les résistances sont en parallèle.
Nous allons voir que c’est un peu « l’inverse » de ce que l’on a dit sur les résistances en série.

Reprenons le schéma avec 3 résistances et mettons les intensités et tensions correspondantes :

On peut tout d’abord remarquer que les intensités qui traversent les résistances ne sont pas les mêmes contrairement aux résistances en série, car il y a un nœud au point A, donc le courant i se divise en trois courants différents.
En revanche, les tensions U₁, U₂ et U₃ sont en fait… égales !

En effet, ces tensions correspondent à une différence de potentiel.
Ici on a U₁ = V_A – V_B, U₂ = V_A – V_B et U₃ = V_A – V_B
Donc U₁ = U₂ = U₃ !

Finalement on peut simplifier le schéma précédent :

La tension U correspond à la tension aux bornes de chaque résistance, la loi d’ohm s’écrit donc :
U = R₁i₁ = R₂i₂ = R₃i₃

Là encore cela nous permet de trouver i₁ par exemple, en connaissant R₁, R₂ et i₂ mais sans connaître la valeur de U.

Ainsi, quand les résistance sont en série, l’intensité est la même mais les tensions différentes, alors que quand elles sont en parallèle, les intensités sont différentes mais la tension est la même.

Tout comme pour les résistances en série, on va pouvoir regrouper les résistances en parallèle en une résistance équivalente R_éq.
Cependant, R_éq ne sera PAS égal à la somme des résistances !
C’est l’inverse de R_éq (1/R_éq) qui sera égal à la somme de l’inverse des résistances.

On aura donc :

Pour trouver R_éq il faut d’abord mettre au même dénominateur puis inverser :

Ce petit calcul sera très souvent effectué, surtout avec deux résistances.
Imaginons en effet que l’on ait que deux résistances en parallèle et non trois, cela donne :

Cette formule n’est pas à apprendre par cœur, il faut la redémontrer à chaque fois, mais elle est plutôt simple à retenir.
Cependant, beaucoup d’élèves mélangent et ne savent plus si R₁R₂ est au numérateur ou au dénominateur.
Pour se souvenir il existe un moyen très simple : les unités !
En effet, R₁R₂ est en Ω², tandis que R₁ + R₂ est en Ω.
Ainsi, comme R_éq est en Ω, il faut des Ω² divisés par des Ω et non l’inverse, donc R₁R₂/(R₁ + R₂).
Il s’agit d’un petit moyen très simple de ne pas se tromper (nous reparlerons de cela dans les exercices).

—
A retenir : pour les résistances en parallèle, l’inverse de la résistance équivalente est égale à la somme des inverses des résistances regroupées.
—

On a donc le schéma suivant :

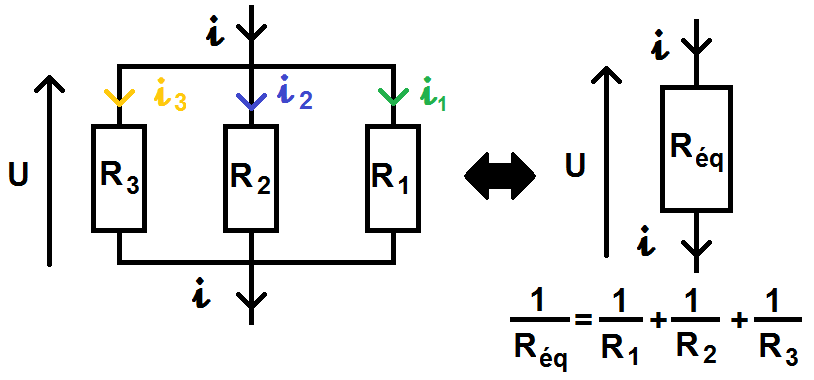
Nous verrons dans les exercices comment utiliser tout ce que l’on vient de voir sur les résistances en série et en parallèle !

Ampèremètre et voltmètre

Haut de page

Dans le chapitre sur les bases de l’électricité, nous avions vu comment brancher un ampèremètre et un voltmètre pour mesurer l’intensité et la tension aux bornes d’un dipôle.
Nous allons faire ici quelques précisions par rapport à cela.

Voyons le branchement classique de ces deux appareils dans un circuit simple :

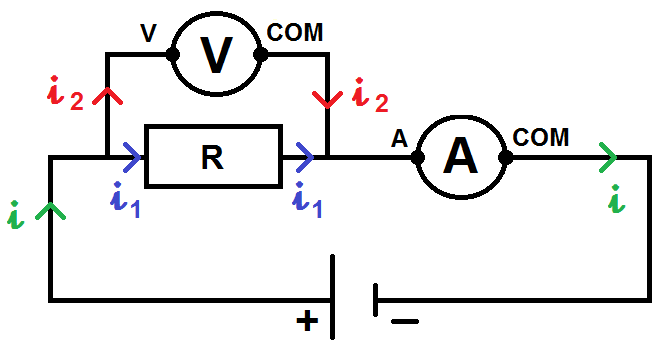
L’ampèremètre mesure bien le courant i délivré par le générateur.
En revanche, à cause du voltmètre il y a un nœud de chaque côté de la résistance, ce qui fait que le courant i₁ qui traverse la résistance n’est pas égal à celui mesuré par l’ampèremètre !! C’est fâcheux…
En effet, d’après la loi des nœuds, on a i = i₁ + i₂ et non i = i₁.

Pour que cela soit le cas, on pourrait enlever le voltmètre (1ère solution très simple…), mais si on veut connaître en même temps l’intensité et la tension il faut garder les deux.
L’autre solution est que le courant i₂ qui traverse le voltmètre soit nul, ou en tout cas négligeable par rapport à i₁.
Pour ce faire, on considère la résistance interne du voltmètre.
En effet, au sein du voltmètre il y a une résistance que l’on appelle résistance interne, que l’on peut noter r.
Si l’on note U la tension aux bornes du voltmètre, on a d’après la loi d’ohm :

Pour que i₂ tende vers 0, il faut que r tende vers… l’infini !
C’est pour cela que l’on dit que la résistance interne du voltmètre est inifinie.
En réalité ce n’est pas possible d’avoir une résistance infinie, mais on peut prendre une résistance la plus grande possible afin que i₂ soit le plus petit possible et donc négligeable.

Regardons maintenant ce qui se passe pour l’ampèremètre. Notons U_A la tension aux bornes de l’ampèremètre, on a alors :

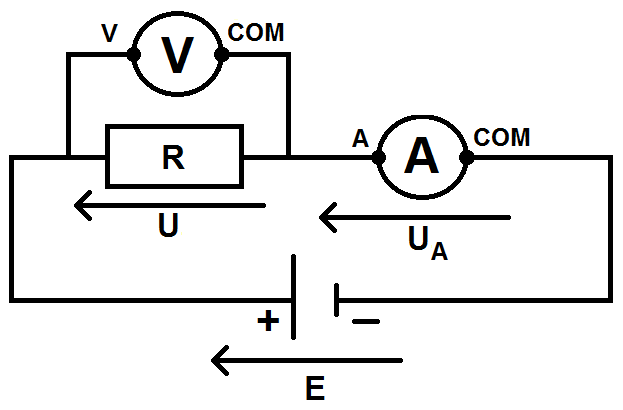
Écrivons la loi des mailles :
E = U + U_A, alors que si on n’avait pas l’ampèremètre on aurait E = U.

La présence de l’ampèremètre influe donc sur la tension aux bornes de la résistance, ce n’est pas ce que l’on veut !
Il faudrait donc que U_A soit nul, ou comme précédemment négligeable par rapport à U.

Tout comme le voltmètre, l’ampèremètre a une résistance interne que l’on va noter r’.
D’après la loi d’ohm, on a U_A = r’i.

Pour que U_A soit le plus petit possible, il faut que r’ soit… le plus petit possible !

—
Ainsi, contrairement à la résistance interne du voltmètre qui doit être la plus grande possible, il faut que la résistance interne de l’ampèremètre soit la plus petite possible.
—

De la même manière que l’on dit le voltmètre est à résistance interne infinie, on dit que l’ampèremètre est à résistance interne nulle (il faut comprendre infinie dans le sens « très grand » et nulle dans le sens « très petit »).

Dernière chose avant de passer aux exercices : tu pourras parfois trouver le montage suivant :

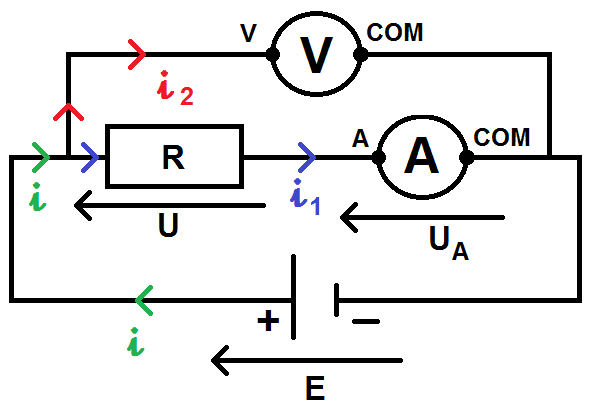
Dans ce montage, l’ampèremètre mesure bien l’intensité i₁ qui traverse la résistance. Le problème est que cette intensité n’est pas celle délivrée par le générateur car une partie du courant passe par le voltmètre…
Mais si comme on l’a dit ci-dessus cette intensité est négligeable, cela règle le problème.

De même, la tension mesurée par le voltmètre n’est pas celle aux bornes de la résistance mais aux bornes de la résistance ET de l’ampèremètre.
Là encore, si la tension aux bornes de l’ampèremètre est négligeable, on peut considérer que la tension mesurée par le voltmètre est bien celle aux bornes de la résistance (approximativement).

Il est temps désormais de passer aux exercices !

Exercices

Haut de page

Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !

Retour au sommaireHaut de la page