Sommaire
Introduction
Pont diviseur de tension
Pont diviseur de courant
Exercices
Nous allons voir dans ce chapitre des formules qui permettent de gagner beaucoup de temps dans l’étude des circuits électriques. Au lieu de faire plusieurs lois des nœuds et des mailles, il suffira d’appliquer la formule (après avoir éventuellement transformé le circuit).
Il faut faire cependant attention à bien adapter les formules aux circuits donnés dans les énoncés, ce n’est pas toujours évident !
C’est en faisant beaucoup d’exercices que tu maîtriseras les ponts diviseurs de tension et de courant.
Le pont diviseur de tension est beaucoup plus utilisé que le pont diviseur de courant, donc entraîne-toi plus sur des exercices faisant intervenir le pont diviseur de tension.
Le schéma général du pont diviseur de tension est le suivant :
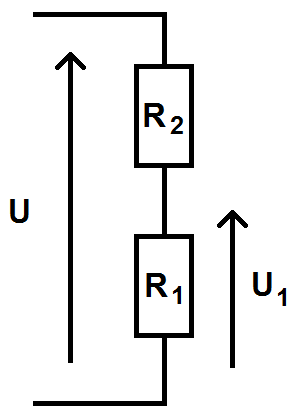
On a deux résistance en série, et on cherche U1, la tension aux bornes d’une résistance, en fonction de la tension U qui est la tension aux bornes des deux résistances.
La formule est alors la suivante :
\(\displaystyle U_1 = \frac{U R_1}{R_1 + R_2} \)
Le principe est le suivant : au numérateur on a la tension « totale » ainsi que la résistance R1 car U1 est la tension aux bornes de R1, et au dénominateur on a la somme des deux résistances.
Si on avait voulu avoir U2, tension aux bornes de R2, on aurait eu d’après ce principe :
\(\displaystyle U_2 = \frac{U R_2}{R_1 + R_2} \)
En effet, les résistances R1 et R2 sont interchangeables car elle sont en série, le principe reste donc le même.
On peut donc compléter le schéma précédent avec les formules :
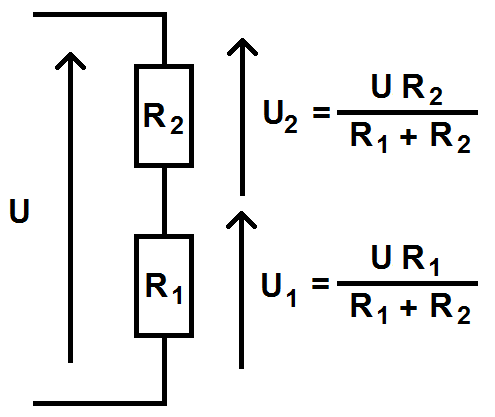
Démontrons cette formule.
Pour ce faire, nous allons utiliser l’intensité i : cette grandeur n’apparaît pas dans les formules mais on va s’en servir comme intermédiaire de calcul.
Pour cela, nous allons faire le circuit équivalent correspondant si l’on regroupe les 2 résistances en série :
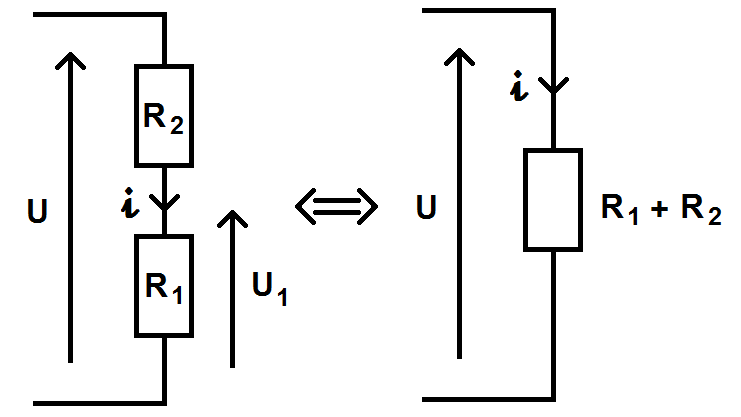
D’après la loi d’Ohm, nous avons :
\(\textstyle U_1 = R_1 i \)
et
\(\textstyle U = (R_1 + R_2)i \)
D’où :
\(\textstyle i = \frac{U_1}{R_1} \)
et
\(\textstyle i = \frac{U}{R_1 + R_2} \)
On a donc :
\(\textstyle \frac{U_1}{R_1} = \frac{U}{R_1 + R_2} \)
D’où la formule :
\(\textstyle U_1 = \frac{U R_1}{R_1 + R_2} \)
Comme tu le vois ce n’est pas très compliqué !
Tu vois également que la formule ne fait intervenir que la loi d’Ohm : ce n’est pas une nouvelle formule, mais cela permet de gagner beaucoup de temps dans les exercices (nous le verrons dans les vidéos) : si on te demande de trouver l’égalité entre U1 et U tu peux utiliser la formule directement, sinon tu aurais été obligé de refaire toute la démonstration.
Comme dit précédemment, il faut évidemment que le schéma que tu as en exercice corresponde au schéma ci-dessus, donc il ne doit pas y avoir de branche en parallèle de R1 ou R2 par exemple (nous verrons dans les exercices comment faire si c’est le cas).
La formule ci-dessus s’applique aux résistances, mais elle peut très bien s’appliquer aux autres dipôles, notamment les bobines et les condensateurs !
Il suffira juste de remplacer R par l’impédance Z de chaque dipôle :
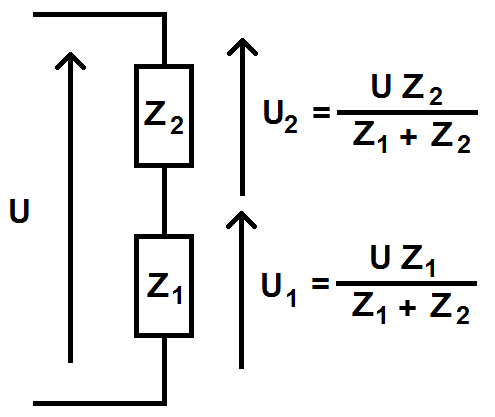
—
On rappelle qu’en régime sinusoïdal forcé, on a :
Z = R pour une résistance
Z = jLω pour une bobine
Z = 1/(jωC) pour un condensateur
—
En Terminale tu ne verras que les résistances donc retiens la formule avec les R c’est suffisant.
Mais il arrive que l’on ait non pas 2 mais plusieurs résistances en série, comment faire dans ce cas-là ?
C’est en fait très simple car on peut généraliser la formule ci-dessus !
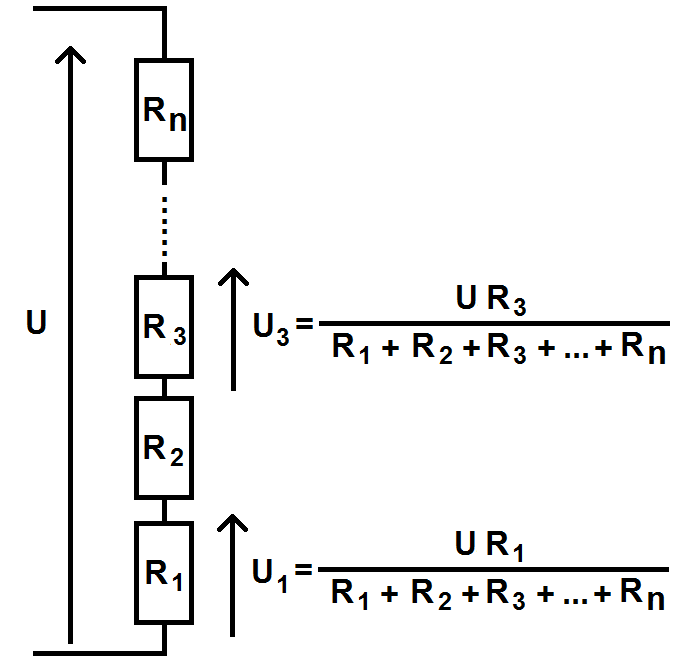
\(\displaystyle U_1 = \frac{U R_1}{R_1 + R_2 + R_3 + … + R_n} \)
si l’on a n résistances en série
Ce qui donne avec les Z :
\(\displaystyle U_1 = \frac{U Z_1}{Z_1 + Z_2 + Z_3 + … + Z_n} \)
La démonstration est quasi similaire à celle effectuée ci-dessus avec 2 résistances, si tu veux tu peux t’entraîner à la faire avec n résistances 
Nous ferons cependant la démonstration avec n résistances mais pour le pont diviseur de courant que l’on va voir… maintenant !
Dans le pont diviseur de courant, les résistances ne sont pas en série mais en parallèle :
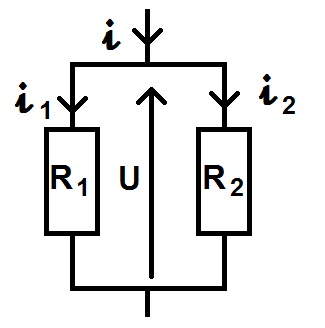
Ici on va chercher la relation entre i1 et i, ou entre i2 et i.
Les formules sont les suivantes :
\(\displaystyle i_1 = \frac{R_2 i}{R_1 + R_2} \)
\(\displaystyle i_2 = \frac{R_1 i}{R_1 + R_2} \)
Comme tu le vois cela ressemble très fortement aux formules du pont diviseur de tension, on a dans les 2 cas R1 + R2 au dénominateur, MAIS dans la formule de i1 c’est R2 au numérateur, et dans la formule de i2 c’est R1 au numérateur…
Cette « inversion » par rapport au pont diviseur de tension n’est pas très pratique car on risque de tout mélanger, on va donc utiliser une autre formule qui permet de faire le parallèle avec le pont diviseur de tension, d’autant plus que cette nouvelle formule sera généralisable contrairement à la formule précédente qui n’est valable que pour 2 résistances…
Cette nouvelle formule utilise l’admittance du dipôle, qui est l’inverse de l’impédance.
L’admittance, notée Y, étant l’inverse de l’impédance Z :
\(\displaystyle Y = \frac{1}{Z} \)
Or pour une résistance on a vu que Z = R, d’où :
\(\displaystyle Y_R = \frac{1}{R} \)
Les formules deviennent alors :
\(\displaystyle i_1 = \frac{Y_1 i}{Y_1 + Y_2} \)
\(\displaystyle i_2 = \frac{Y_2 i}{Y_1 + Y_2} \)
Et cette fois-ci on retrouve les mêmes formules que le pont diviseur de tension mais en remplaçant les U par des i et les Z par des Y !
De plus il n’y a plus « d’inversion », puisque c’est Y1 au numérateur de i1 et Y2 au numérateur de i2…
Vérifions qu’avec cette formule on retrouve celle vue précédemment avec le R :
\(\textstyle i_1 = \frac{Y_1 i}{Y_1 + Y_2} \)
\(\textstyle i_1 = \frac{\frac{1}{R_1} i}{\frac{1}{R_1} + \frac{1}{R_2}} \)
\(\textstyle i_1 = \frac{i}{R_1(\frac{R_2 + R_1}{R_1 R_2})} \)
\(\textstyle i_1 = \frac{i}{\frac{R_2 + R_1}{R_2}} \)
\(\textstyle i_1 = \frac{R_2 i}{R_2 + R_1} \)
On retrouve bien la même formule (heureusement !) 
L’autre intérêt de cette formule est que, comme dans le cas du diviseur de tension, nous allons pouvoir généraliser cette formule dans le cas où l’on aurait plusieurs dipôles en parallèle :
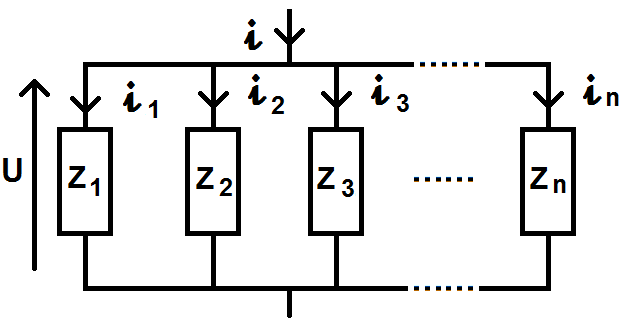
Si l’on a ce genre de schéma, on pourra utiliser la formule :
\(\displaystyle i_1 = \frac{i Y_1}{Y_1 + Y_2 + Y_3 + … + Y_n} \)
On retrouve la même formule de généralisation que pour le pont diviseur de tension mais en remplaçant les U par des i et les Z par des Y.
—
Attention à ne pas mélanger toutes les formules, mais pour ne pas se tromper il existe un moyen très simple : pour les i c’est Y (prononcé i grec) : facile à retenir !
Et donc par déduction pour U c’est Z…
—
Faisons la démonstration de la formule précédente : on sait que quand les résistances sont en parallèles, ce sont les Y qui s’additionnent et non les Z, on a donc le schéma équivalent suivant :
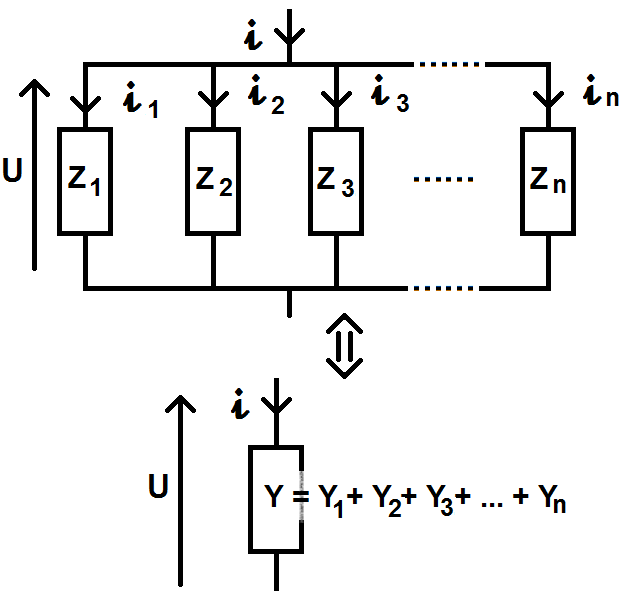
On rappelle que la formule générale est U = Zi ou U = i/Y (puisque Y = 1/Z donc Z = 1/Y)
On a alors :
\(\textstyle U = \frac{i}{Y} \)
et
\(\textstyle U = Z_1 i_1 \)
D’où :
\(\textstyle Z_1 i_1 = \frac{i}{Y} \)
\(\textstyle \frac{1}{Y_1} i_1 = \frac{i}{Y} \)
\(\textstyle i_1 = \frac{Y_1 i}{Y} \)
\(\textstyle i_1 = \frac{Y_1 i}{Y_1 + Y_2 + Y_3 + … + Y_n} \)
Et voilà ! 
Le pont diviseur de courant est certes moins utilisé que le pont diviseur de tension mais peut être très utile dans certains cas !
Tu trouveras sur cette page tous les exercices sur le pont diviseur de courant et de tension !
Retour au sommaireHaut de la page



Merci beaucoup!
Merci !!! Vous venez de me sauver, je pensais cette notion incompréhensible (suite au explication très limitée de mon prof) mais j’ai désormais tout compris et cela me paraît même assez simple. 😁
Synthèse impeccable👌 !
Merci beaucoup pour ces explications claires et enrichissantes😊🙏🏻
Merci et bon courage.
Très enrichissant
Merci ! Mon problème a été résolu
👍👍👍
Génial, j’ai eu tout ce que je voulais!
Bonjour,
Merci pour le cours.
Attention il y’a une erreur dans la formule de i2 pour le pont diviseur de courant. (i2 = Y2*I / (Y1+Y2))
Cordialement,
B moop
Merci ! L’erreur a été corrigée.
Merci beaucoup j’ai compris des truc où j’avais beaucoup de mal alors qu’en vrai c’est super simple. MERCI
C’est bien complet. Merci beaucoup
Très satisfaisant, cet article m’a vraiment aidé
Merci ! 🙂