Exercices corrigés sur les ondes

Sommaire

Récepteur et émetteur qui s’éloignent
Le sonar
Les années-lumière
La méthode d’Ératosthène

Les exercices ci-dessous sont souvent inspirés de sujets du BAC.
N’hésite pas à aller d’abord voir le cours sur les ondes avant de faire les exercices

Récepteur et émetteur qui s’éloignent

Cet exercice est inspiré de l’exercice 3 du BAC Asie de 2007.
On a un émetteur qui émet des ondes sonores.
On dispose de deux récepteurs R₁ et R₂ espacés de 2,8 cm selon le schéma suivant :

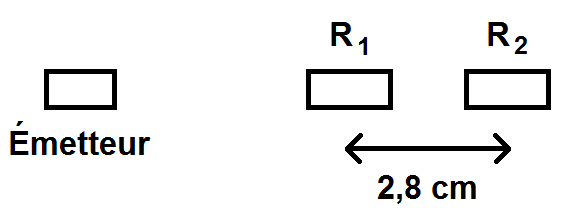
Un dispositif permet de visualiser le signal par R₁ et R₂. On obtient la figure suivante :

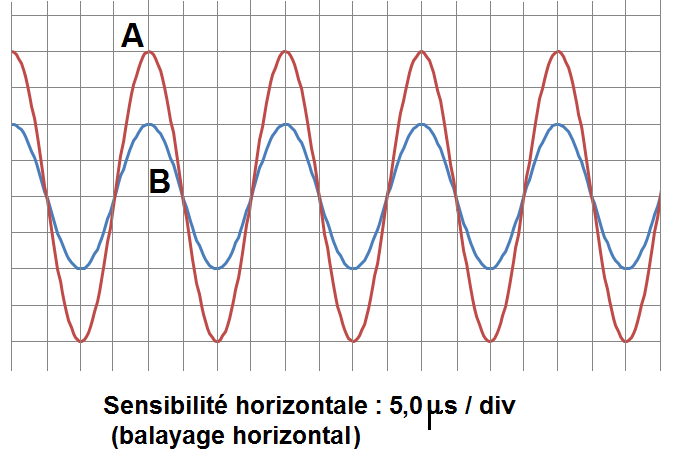
1) Identifier chaque courbe (on note A la courbe rouge et B la courbe bleue).
2) Déterminer la fréquence f de l’onde.
On écarte progressivement le récepteur R₂ de R₁ jusqu’à avoir à nouveau les ondes A et B en phase pour la première fois. On a alors éloigné R₂ de 0,70 cm.
3) Déterminer la longueur d’onde λ de l’onde.
4) Déterminer la vitesse v de l’onde.
5) Tracer sur le graphique ci-dessus le signal de l’onde reçue au niveau de la nouvelle position de R₂.
6) Faire de même si on avait éloigné R₂ non pas de 0,70 cm mais de 0,35 cm.

Le sonar

Haut de page

Cet exercice est inspiré de l’exercice 2 du BAC Amérique du Nord de 2007.

On considère un bateau équipé d’un sonar au niveau de l’eau.
Ce sonar émet une onde vers le fond de l’océan. Cette onde se réfléchit sur le fond de l’océan et est ensuite reçue par un récepteur situé au même niveau que le sonar.
On note p la profondeur de l’océan :

Un dispositif permet de visualiser l’onde émise et l’onde reçue :

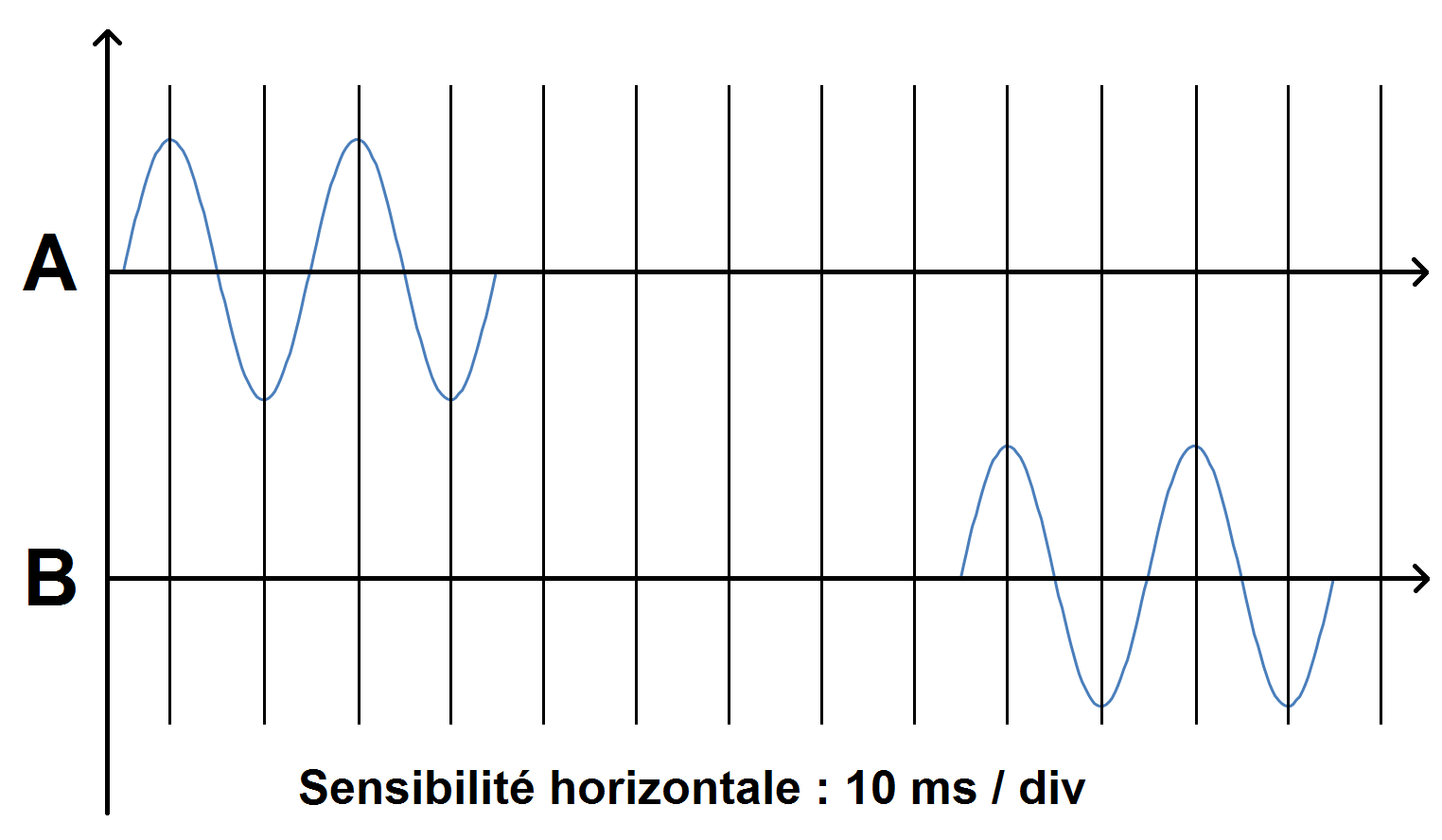
1) Identifier chaque signal.
2) Déterminer la durée Δt entre l’émission et la réception du signal.
3) Déterminer la profondeur p.
Donnée : v_son = 1500 m.s^-1

Les années-lumière

Haut de page

On considère que la distance entre la Terre et le Soleil est d_TS = 150 millions de km.
La célérité de la lumière est c = 300 millions de m/s
1) Calculer en minutes le temps que met la lumière du Soleil pour arriver sur Terre.
2) Que vaut 1 année-lumière, notée a.l.
3) Proxima du Centaure, l’étoile la plus proche de la Terre, est située à 4,3 a.l. de la Terre. Convertir cette distance en mètres.

Méthode d’Ératosthène

Haut de page

dans l’Antiquité, Ératosthène a réussi à donner une valeur approchée du rayon de la Terre. Nous allons développer ici la méthode qu’il a utilisée.
Il s’est rendu compte qu’à midi, le Soleil était au zénith à Syène, mais au même moment à Alexandrie, un bâton de 1 mètre planté verticalement avait une ombre de 12,3 cm.
Pour aller de Syène à Alexandrie, il fallait à l’époque 50 jours à dos de chameau, sachant qu’un chameau peut parcourir 100 stades par jour (1 stade = 160 m).
1) Faire un schéma de la situation.
2) A partir de ces éléments et du schéma, calculer la rayon de la Terre.

Retour au coursHaut de la page