Exercices corrigés de thermodynamique

Sommaire

Introduction
Mélange de deux corps
Eau chaude + eau froide
Cycle et rendement de Carnot
Cycle Beau de Rochas
Détente de Joule-Gay Lussac
Mélange d’eau et de glace
Une masse, un piston et du chauffage

Introduction

Nous allons voir dans ce chapitre quelques exercices d’application classiques de thermodynamique, en particulier du premier principe, qui peuvent être considérés comme du cours.
Tu dois impérativement savoir les refaire car il s’agit d’exemples revenant régulièrement en exercice et en contrôle.
Il est fortement conseillé évidemment d’après au préalable lu le chapitre sur le premier principe avant de faire les exercices ci-dessous.

Mélange de deux corps

Haut de page

Énoncé :
On considère une boîte aux parois athermanes initialement séparée en deux parties par une paroi qui ne peut pas glisser mais amovible.
La partie de gauche contient un gaz de masse m_a, de température T_a et de capacité calorifique massique c_a.
La partie de droite contient un gaz de masse m_b, de température T_b et de capacité calorifique massique c_b.
On suppose que les gaz ne subissent pas de changement d’état et que leur capacité calorifique ne dépend pas de la température.

On enlève alors la paroi séparatrice (sans que cela n’engendre de travail) : calculez alors la température finale T_f du milieu.
Vérifiez que des cas particuliers sont en accord avec l’expression trouvée.

Solution :
On considère comme système les deux gaz. La paroi étant athermane, il n’y a pas d’échange de chaleur avec l’extérieur, donc Q = 0.
Il y a en revanche des transferts thermiques entre les deux gaz, on notera Q₁ celui subi par le gaz de gauche et Q₂ celui subi par le gaz de droite.
On a donc Q = Q₁ + Q₂
D’où Q₁ + Q₂ = 0
Le gaz de gauche subit un changement de température de T_a à T_f, le gaz de droite subit un changement de température de T_b à T_f, d’où :

Les capacités calorifiques étant indépendantes de la température d’après l’énoncé :

En isolant T_f, on obtient :

On vérifie très facilement que cette formule est bien homogène (tu peux t’entraîner à le faire).
De plus, vérifions comme le demande l’énoncé, que certains cas particuliers sont bien conformes à l’expression trouvée.

Tout d’abord, si T_a = T_b : les températures initiales étant identiques, la température finale ne devrait pas changer.

La température finale est bien égale à la température initiale.

2ème cas particulier : si les deux gaz sont les mêmes (c_a = c_b), en même quantité (m_a = m_b) mais de température différente : la température finale devrait être la moyenne des 2 températures :

On retrouve bien que la température finale est la moyenne des deux températures.

La formule trouvée est donc bien compatible avec ces deux cas particuliers.

Eau chaude + eau froide

Haut de page

On dispose de deux quantités d’eau de masse m₁ et m₂, de température T₁ et T₂ et de volume V₁ et V₂.
On mélange ces deux quantités d’eau dans un troisième récipient.
Donner la température finale du mélange en fonction de m₁, m₂, T₁ et T₂, puis en fonction de V₁, V₂, T₁ et T₂.

Cycle et rendement de Carnot

Haut de page

On considère un gaz parfait subissant le cycle de Carnot composé des 4 phases suivantes :
– de 1 à 2 : détente isotherme à la température T_c (Q_c)
– de 2 à 3 : détente adiabatique réversible pour amener à la température T_f
– de 3 à 4 : compression isotherme à la température T_f (Q_f)
– de 4 à 1 : compression adiabatique réversible pour revenir à la température T_c

1) Tracer le diagramme de Clapeyron correspondant.
2) Calculer le rendement de ce cycle.
3) Montrer qu’il s’agit du rendement maximal pour un moteur appelé rendement de Carnot.

Cycle Beau de Rochas

Haut de page

On considère un gaz parfait subissant le cycle Beau de Rochas composé des 4 phases suivantes :
– de 1 à 2 : compression adiabatique réversible pour amener à V_min
– de 2 à 3 : combustion isochore pour amener à Q_c
– de 3 à 4 : détente adiabatique réversible pour amener à V_max
– de 4 à 1 : refroidissement isochore pour amener à Q_c

On définit le taux de compression volumétrique par :

1) Tracer le diagramme de Clapeyron correspondant.
2) Calculer le rendement de ce cycle en fonction de α et γ.

Détente de Joule Gay-Lussac

Haut de page

Énoncé :
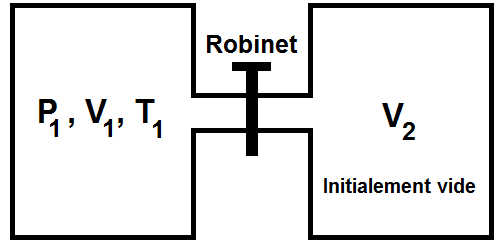
On considère un gaz parfait enfermé dans un récipient de volume V₁, à la température T₁ et à la pression P₁.
Ce récipient est relié à un volume V₂ initialement vide par un robinet.
Les parois de l’ensemble sont indéformables et calorifugées.
On ouvre rapidement le robinet, de sorte que le gaz se répartit dans tout le volume.

1) Cette transformation est-elle réversible ?
2) Calculer Q et W échangés avec l’extérieur.
3) En déduire ΔU et la température finale T_f du gaz.
4) Calculer la pression finale P_f du gaz.

Solution :
1) On ouvre rapidement le robinet, donc le gaz se répartit rapidement dans le volume V₂ : cette rapidité fait que la transformation est irréversible.

2) Les parois de l’ensemble sont calorifugées d’après l’énoncé, donc Q = 0.
De plus, les parois sont indéformables, donc dV = 0, d’où W = 0.

3) D’après le premier principe, ΔU = W + Q, donc ΔU = 0.
Le gaz étant un gaz parfait, ΔU = C_vΔT, donc ΔT = 0.
On a donc T_f = T₁.

4) Le gaz étant parfait, on a à l’état initial :

A l’état final, V_f = V₁ + V₂ et T_f = T₁ :

D’où :

La transformation décrite dans l’énoncé est ce que l’on appelle une détente de Joule Gay-Lussac.

Mélange d’eau et de glace

Haut de page

Énoncé :
On considère une boîte calorifugée contenant m₁ = 200 g d’eau liquide à T₁ = 25°C.
On y ajoute un glaçon de masse m₂ = 5,00 g à T₂ = -10°C.
Calculer la température finale T_f.
Données :
– chaleur latente de fusion de la glace : L = 334 kJ.kg^-1
– capacité calorifique massique de l’eau liquide : c_liq = 4186 J.kg^-1.K^-1
– capacité calorifique massique de la glace : c_g = 2090 J.kg^-1.K^-1

Solution :
On considère la système {eau liquide + glace} : les parois étant calorifugées, Q = 0.
Mais il y a transfert thermique entre l’eau et la glace : soit Q₁ celui relatif à l’eau liquide et Q₂ celui relatif à la glace : Q = Q₁ + Q₂.
Donc Q₁ + Q₂ = 0.

Faisons l’hypothèse que la température finale sera supérieure à 0°C : le glaçon va entièrement fondre puis se réchauffer, tandis que l’eau liquide va uniquement subir un refroidissement :
Q₁ = m₁c_liq(T_f – T₁)
Pour le glaçon :
– sa température va d’abord augmenter jusqu’à 0°C : m₂c_g(0 – T₂)
– puis il va fondre : m₂L
– et ensuite se réchauffer jusqu’à T_f : m₂c_liq(T_f – 0). On a donc :
Q₂ = m₂c_g(0 – T₂) + m₂L + m₂c_liq(T_f – 0)
Q₂ = m₂(-c_gT₂ + L + c_liqT_f)

On regroupe le tout :

En isolant T_f, on trouve :

En remplaçant avec les données (attention à bien mettre les degrés en Kelvin !), on trouve :

L’hypothèse de départ selon laquelle la température finale était supérieure à 0°C est donc bien vérifiée.

La température trouvée de 19°C est plutôt logique car on mélange un glaçon de 5 g à -10°C avec 200 g d’eau à 25 °C.

On pourrait faire le même exercice mais avec un glaçon plus gros par exemple, et on trouverait alors une température finale négative : l’hypothèse de départ serait alors fausse et il faudrait recommencer en faisant l’hypothèse selon laquelle l’eau liquide va aller à 0°C et une partie va se transformer en glace, et le glaçon va lui aussi aller à 0°C.
Tu peux t’entraîner à faire cet exercice !

Une masse, un piston et du chauffage

Haut de page

Les exercices avec masse et piston sont assez courants en thermodynamique. En voici un assez classique, tu pourras trouver des énoncés légèrement différents mais similaires.

Énoncé :
On considère un cylindre aux parois athermanes fermé par un piston. Le piston (en rouge sur le schéma), de section S et de masse négligeable, peut glisser sans frottement entre 2 cales A et B.
Dans l’état initial, le piston est en A, le cylindre renferme un volume V_A d’air supposé gaz parfait, à la température extérieure T₀, pression P₀, (gaz dans l’état 0 : P₀, V_A, T₀).

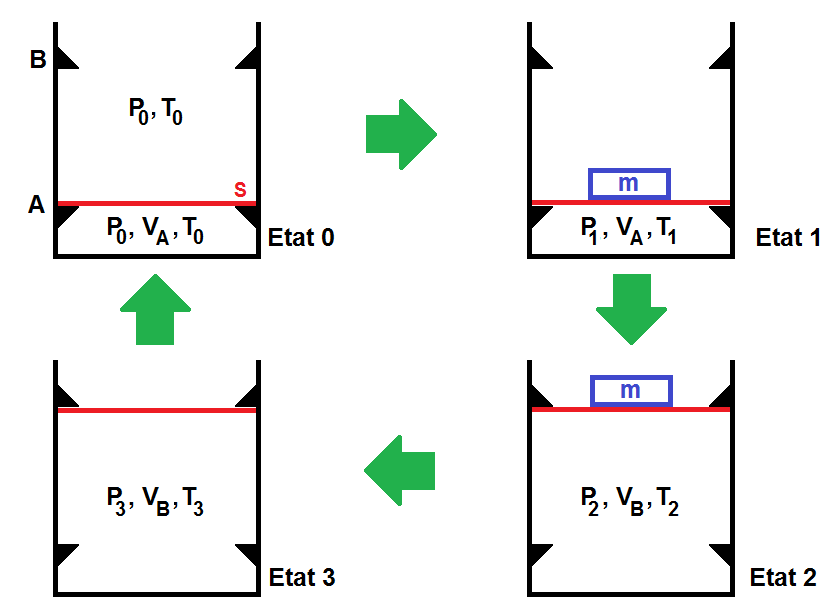
On place une masse m (en bleu sur le schéma) sur le piston et on chauffe très doucement le gaz par un dispositif non représenté sur le schéma, jusqu’à ce que le piston décolle tout juste de la cale A (gaz dans l’état 1 : P₁, V_A, T₁).
On maintient alors le chauffage jusqu’à ce que le piston arrive tout juste en B (gaz dans l’état 2 : P₂, V_B, T₂), le chauffage est alors arrêté.
On enlève alors la masse m et on laisse refroidir l’ensemble jusqu’à ce que le piston décolle tout juste de B (gaz dans l’état 3 : P₃, V_B, T₃). On laisse refroidir jusqu’à la température T₀ : le piston revient en A (le gaz est revenu dans l’état 0), le cycle est terminé.
Données : V_B = 1,0 L, V_A = 330 mL
T₀ = 300 K, P₀ = 1,0 bar
m = 10 kg, S = 100 cm², g = 10 m.s^-2, R = 8,314 J.K^-1.mol^-1.

1) Quelle est la caractéristique commune à toutes les transformations ?
2) Quelle est la nature de la transformation de 0 à 1 subie par le gaz ?
3) Exprimer puis calculer la pression P₁ et la température T₁ en fonction de P₀, T₀, m, g et S.
4) Quelle est la nature de la transformation de 1 à 2 ?
5) Exprimer et calculer T₂ en fonction de T₁, V_A et V_B.
6) Exprimer le travail W_1,2 reçu par le gaz lors de cette transformation en fonction de P₁, V_B et V_A.
7) Quelles sont les natures des transformations de 2 à 3 et de 3 à 0 ?
8) Exprimer les travaux W_2,3 et W_3,0 en fonction de P₀, V_B et V_A.
9) Exprimer puis calculer le travail W échangé par le système avec l’extérieur au cours du cycle, en fonction de m, g, V_A, V_B, et S. Commenter le signe de W.
10) Tracer l’allure du diagramme de Clapeyron d’un cycle.
11) Retrouver l’expression du travail W avec le diagramme.

Solution :

1) Le piston se déplace sans frottement et les transformations se font lentement, on peut donc supposer qu’elles sont toutes réversibles.

2) La transformation de 0 à 1 subie par le gaz est une isochore (car volume constant) : on peut préciser isochore réversible.

3) Pour cette question, on va utiliser le fait qu’au moment où le piston décolle à peine, il y a équilibre mécanique : la force due à la cale n’est plus prise en compte puisqu’il n’y a plus contact (ce qui n’était pas le cas avant).
Le piston est soumis au poids de la masse (son propre poids est négligeable d’après l’énoncé), aux forces dues à la pression (pression P₁ de l’air enfermé qui pousse vers le haut, et pression de l’air P₀ dirigée vers le bas).
On avait vu dans le cours que ces forces s’expriment F = P × S, avec S la surface de contact.
D’après la deuxième loi de Newton appliquée au piston :

En projetant sur l’axe vertical, on obtient :

Comme on a P₁, avec la loi des gaz parfaits on pourrait trouver T₁ mais d’après l’énoncé on ne veut pas le volume V_A dans l’expression.
Cependant, on sait que la transformation est isochore, on va donc appliquer la loi des gaz parfait à l’état 0 et à l’état 1 :

En faisant le rapport des deux équations :

On remplace alors P₁ par l’expression trouvée précédemment :

4) La transformation de 1 à 2 est réversible, donc à chaque instant il y a équilibre mécanique, donc la pression du gaz vaut P₁. On a ainsi P₂ = P₁.
La transformation est donc isobare (on peut préciser isobare réversible).

5) D’après la loi des gaz parfaits dans l’état 1 et 2, on a :

En faisant le rapport des deux équations comme précédemment, on obtient :

6) La transformation est isobare à la pression P₁, donc d’après le cours :

7) La transformation de 2 à 3 est isochore car volume constant V_B (on peut préciser isochore réversible).
Tout comme à la question 4, la transformation de 3 à 0 est réversible donc à chaque instant il y a équilibre mécanique, donc la pression du gaz vaut P₀ (puisqu’elle vaut P₀ à l’état 0). La transformation de 3 à 0 est donc isobare.

8) La transformation de 2 à 3 est isochore donc W_2,3 = 0.
La transformation de 3 à 0 est isobare à la pression P₀, donc de même qu’à la question 6 :

9) Le travail sur tout le cycle est la somme des travaux des différentes transformations, donc :

W_0,1 = 0 car transformation isochore (c’est le seul qui n’était pas demandé dans l’énoncé) :

W est négatif : il cède du travail à l’extérieur (plutôt logique car il reçoit de l’énergie sous forme thermique).

10) Le cycle est constitué de deux isochores (0-1 au volume V_A et 2-3 au volume V_B) qui seront représentées verticalement dans le diagramme de Clapeyron, et de deux isobares (1-2 à la pression P₁ et 3-0 à la pression P₀) qui seront représentées horizontalement.
De plus, V_A < V_B et P₀ < P₁, donc on a :

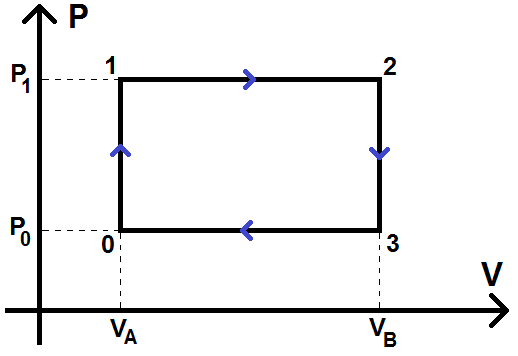
11) Le cycle est décrit dans le sens des aiguilles d’une montre, donc le travail est égal à l’opposé de l’aire du cycle :

Or il s’agit d’un rectangle, dont les côtés valent (V_B – V_A) et (P₁ – P₀), donc :

On retrouve bien l’expression trouvée précédemment par le calcul !

Exercices

Haut de page

Les exercices sur ce chapitre seront bientôt disponibles !

Sommaire des coursHaut de la page