Sommaire
Introduction
Diagramme d’énergie
Les photons
Les transitions énergétiques
Etat d’ionisation
Exemples d’application
Exercices
Nous allons voir dans ce cours ce que l’on appelle les niveaux d’énergie d’un atome. En effet, chaque atome a une énergie, et on va pouvoir représenter cela par un diagramme (et faire des calculs par la même occasion  ).
).
Avant de commencer nous allons faire une remarque TREEEEEEEES importante.
Dans ce chapitre nous allons souvent parler de la fréquence, qui se note f (f comme fréquence).
Mais pour ce chapitre, les livres ne notent pas la fréquence f mais

Cette lettre qui se prononce « nu » ressemble à un v mais penché et à la fin on remonte le stylo. Le problème est que cette lettre ressemble justement à un v et on pourrait confondre avec la vitesse (surtout que l’on va parler de la vitesse de la lumière dans ce chapitre…).
Ainsi, même en classe il est fort possible que ton professeur note la fréquence mais nous la noterons f (ce qui est bien plus logique).
Cependant, si dans l’énoncé elle est marquée tu devras respecter cela et ne pas la noter f… il faut t’adapter à l’énoncé !
Après cette remarque préliminaire, rentrons dans le vif du sujet !
Le diagramme d’énergie d’un atome ressemble à cela :
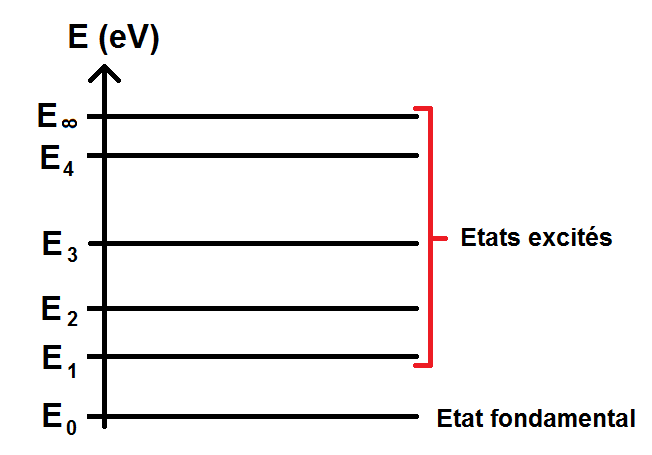
On peut également avoir cela :
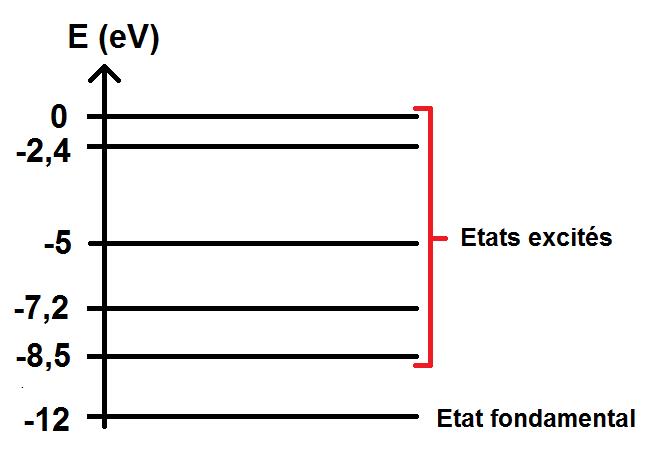
On peut déjà faire plusieurs remarques :
– chaque trait horizontal correspond à un niveau d’énergie. Cette énergie est en eV (électronvolts) mais dans les formules que l’on verra plus tard elle devra absolument être en Joules !!
Dans le diagramme on la met en eV pour avoir des chiffres « sympathiques », comme tu le vois compris entre 0 et -20 environ. Si on avait laissé en Joules, on aurait eu du 10-19 ce qui n’est pas terrible…
On rappelle en effet que 1 eV = 1,6 × 10-19 J (cela n’est pas à apprendre par cœur ce sera généralement rappelé dans l’énoncé).
– par ailleurs, le niveau d’énergie le plus bas est appelé l’état fondamental, les autres niveaux sont appelés des états excités. Retiens bien cela car il est souvent demandé en question de cours le nom des niveaux d’énergie !!
L’état fondamental correspond à l’état où l’atome est au repos.
– tu as remarqué que ces niveaux avaient un nom : E0, E1, E2 etc… Sache tout d’abord que l’état fondamental n’est pas nécessairement E0, ça peut très bien être E1 (cela dépend des énoncés).
Dans l’exemple nous sommes allés jusqu’à E4 mais tu peux très bien aller jusqu’à E5, E6 etc…
– il y a un niveau particulier qui est E∞, qui correspond à 0 eV. C’est ce qu’on appelle l’état d’ionisation (nous y reviendrons plus tard). Ce qui est important c’est qu’il correspond à 0 eV, donc l’énergie des autres niveaux est… négative, comme tu le vois sur le diagramme !
Cela est dû au fait que l’on considère les électrons de l’atome, qui gravitent autour du noyau (voir le chapitre sur les atomes pour plus de précisions), et qui sont négatifs (nous allons en parler juste après).
Cependant il arrive parfois que l’on ait un diagramme avec des énergies positives, cela ne change rien aux calculs que l’on verra plus tard.
– enfin, l’énergie de l’atome est quantifiée. Cela signifie que l’atome ne peut prendre que certaines valeurs d’énergie bien particulières qui correspondent aux niveaux d’énergie du diagramme. Ainsi dans l’exemple l’atome pourra avoir une énergie de -7,2 eV ou -8,5 eV mais pas -7,8 eV car il n’y a pas de niveau d’énergie à -7,8 eV !
Très souvent en contrôle ou au bac on te demandera d’expliquer ce que signifie la quantification de l’énergie. Tu devras alors répondre que l’énergie d’un atome ne peut prendre qu’un certain nombre de valeurs correspondant aux niveaux d’énergie.
Maintenant que nous avons vu toutes ces caractéristiques, parlons un peu des photons avant de voir l’intérêt de ce diagramme.
Un photon est une particule d’une onde (ou d’une radiation). La lumière par exemple est constituée de photons.
Ces photons ont une certaine énergie E qui dépend de la fréquence de l’onde ou de la radiation (celle que l’on notera f mais qui est souvent noté .
On a la relation :
\(\displaystyle E = h f \)
que tu trouveras dans les livres sous la forme :
\(\textstyle E = h \nu \)
h est la constante de Planck, h = 6,63 × 10-34 J.s (pas à connaître par cœur, elle est donnée dans l’énoncé)
f est la fréquence de l’onde (en Hz)
E est l’énergie du photon (attention en Joules !!!!, pas en eV…)
Cette formule est à connaître impérativement !!!
Mais on va pouvoir la transformer un peu 
En effet, on a vu dans le chapitre sur les ondes que, en notant c la célérité de la lumière dans le vide, λ la longueur d’onde et T la période (avec T = 1/f), on a :
\(\textstyle c = \frac{\lambda}{T} \)
\(\textstyle c = \lambda \times f \)
D’où :
\(\textstyle f = \frac{c}{\lambda} \)
En remplaçant dans la formule vue plus haut, on obtient :
\(\displaystyle E = h \frac{c}{\lambda} \)
Cette 2ème formule est également à apprendre par cœur ! (même si tu peux la retrouver avec la petite démonstration que l’on vient de faire).
Dans cette formule, E et h sont les mêmes qu’avant.
c est la célérité de la lumière dans le vide (3,00 × 108 m.s-1)
λ est la longueur d’onde de l’onde (en mètres).
Ainsi nous avons deux formules pour l’énergie du photon. Pour savoir laquelle utiliser, tout dépend de ce que tu as ou ce que tu cherches dans l’énoncé !
Si tu as la fréquence, tu vas utiliser la 1ère formule. Si tu as la longueur d’onde, tu vas utiliser la 2ème formule.
Idem si on te demande la fréquence, tu vas utiliser la 1ère formule, si on te demande la longueur d’onde, tu vas utiliser la 2ème formule.
Mais à quoi vont servir ces photons ??
Comme on vient de le voir un photon correspond à une certaine énergie. Réciproquement, une énergie correspond à un photon.
L’idée est que l’on a un électron qui se situe sur un niveau d’énergie. Cet électron (en rouge sur les schémas) va pouvoir aller sur un autre niveau, n’importe lequel (c’est ce que l’on appelle une transition énergétique). Cette transition se matérialise par une flèche :
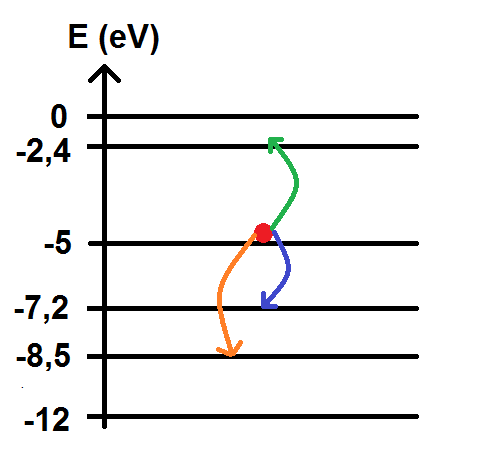
Sur le schéma on a représenté 3 transitions énergétiques différentes.
On remarque que ces transitions peuvent se faire vers un niveau d’énergie plus élevé (en vert) ou moins élevé (en bleu et en orange).
Pour que l’électron aille vers un niveau d’énergie plus élevé, il faut qu’il gagne de l’énergie. Cette énergie correspond à la différence d’énergie entre le niveau de départ et le niveau d’arrivée.
Cette énergie, notée ΔE, est donc égale, dans notre exemple, à la différence des deux énergies, soit – 2,4 – (- 5) = 2,6 eV.
Ainsi, pour la transition verte, ΔE = 2,6 eV.
Pour obtenir un résultat positif, il faut toujours faire l’énergie la plus haute (la plus proche de 0) moins l’énergie la plus basse.
Sinon, pour être sûre d’avoir un résultat positif, on met souvent une valeur absolue sans se préoccuper de la plus grande énergie et de la plus petite.
Ainsi, quand un électron passe d’un niveau A à un niveau B (en montant ou en descendant), on a :
\(\displaystyle \Delta E = |E_B – E_A| \)
Remarque : vu que l’on prend la valeur absolue, on pend très bien dire ΔE = |EA – EB|
Mais d’où va venir cette énergie que l’électron doit acquérir ?
Tout simplement d’un photon !
L’électron va absorber un photon d’énergie ΔE afin de pouvoir aller sur le niveau supérieur.
Mais attention !! L’énergie de ce photon doit être EXACTEMENT celle de ΔE !!!
Dans l’exemple on avait ΔE = 2,6 eV. Si le photon a une énergie de 2,8 eV, il ne se passera… rien du tout ! L’électron va rester sur son niveau d’énergie (on pourrait penser qu’il va prendre 2,6 eV et laisser les 0,2 restant mais non…).
Cela est dû au fait que l’énergie est quantifiée : l’électron étant au départ sur le niveau -5 eV, s’il absorbe le photon d’énergie 2,8 eV il va se retrouver à -2,2 eV, ce qui ne correspond à… aucun niveau d’énergie, donc il ne va rien se passer^^
Le ΔE de la transition énergétique correspond donc à l’énergie du photon, dont on a vu la formule précédemment !
Ainsi, on a :
\(\textstyle \Delta E = h f \)
ou bien
\(\textstyle \Delta E = h \frac{c}{\lambda} \)
A partir de cela on peut calculer la fréquence ou la longueur d’onde de la radiation correspondant au photon.
C’est généralement ce genre de calculs que tu auras à faire en exercice 
L’absorption de ce photon est matérialisé sur le diagramme de la manière suivante :
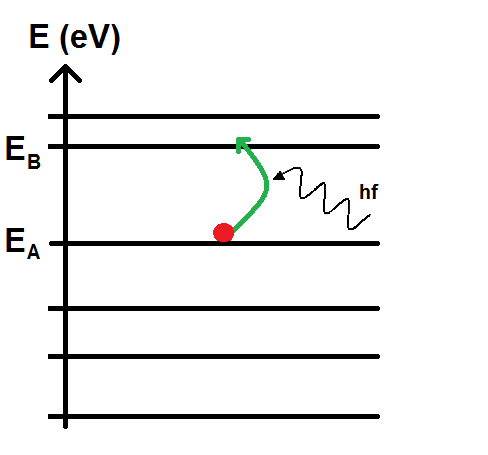
Ce petit signe signifie pour que pour passer d’un niveau à l’autre, l’électron va absorber un photon d’énergie E = hf.
A l’inverse, si l’électron passe à un niveau inférieur, donc d’énergie moins élevée, il va perdre de l’énergie. Cette énergie va se transformer en photon : l’électron va émettre un photon et non l’absorber.
L’énergie de ce photon est aussi égale à la différence d’énergie entre les deux niveaux, les calculs et les formules sont donc strictement identiques.
Cette émission ce note sur le diagramme de la manière suivante :
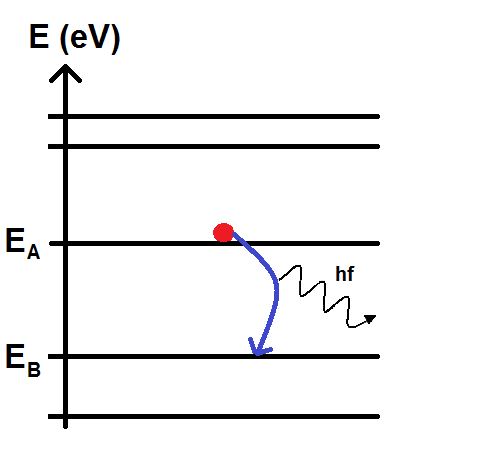
Comme tu le vois c’est la même chose mais cette fois-ci la flèche va dans l’autre sens (normal puisque c’est l’électron qui émet le photon).
Comme pour l’absorption, l’énergie du photon émis sera égale à la différence d’énergie entre les deux niveaux d’énergie.
Avec les formules, cela va permettre de connaître la fréquence et la longueur d’onde du photon émis et de la radiation correspondante.
Ainsi, si l’on récapitule :
Pour passer d’un niveau A à un niveau supérieur B, l’électron doit absorber un photon d’énergie EXACTEMENT ÉGALE à ΔE.
On a alors ΔE = hf.
Quand il passe d’un niveau A à un niveau inférieur B, l’électron va émettre un photon d’énergie égale à ΔE.
On a alors ΔE = hf :
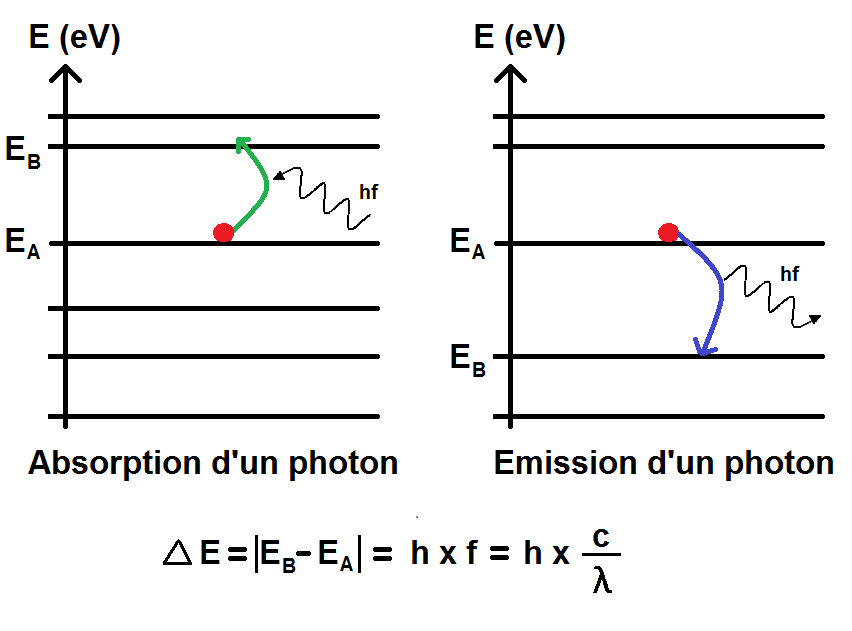
Avant de passer aux exemples d’application, revenons sur l’état d’ionisation dont on a parlé plus haut.
Nous avions vu qu’il existe un niveau d’énergie particulier : E∞, qui correspond à 0 eV.
Il s’agit de l’état d’ionisation.
Si l’électron arrive à ce niveau d’énergie, il ne sera plus lié à l’atome, l’atome va donc perdre cet électron : il va devenir un ion, d’où le nom d’état d’ionisation ! (ou état ionisé).
Nous avions vu dans le chapitre sur les ions que les électrons d’un atome étaient répartis en couches électroniques.
En première approximation, on peut dire que chaque niveau d’énergie correspond à une couche électronique.
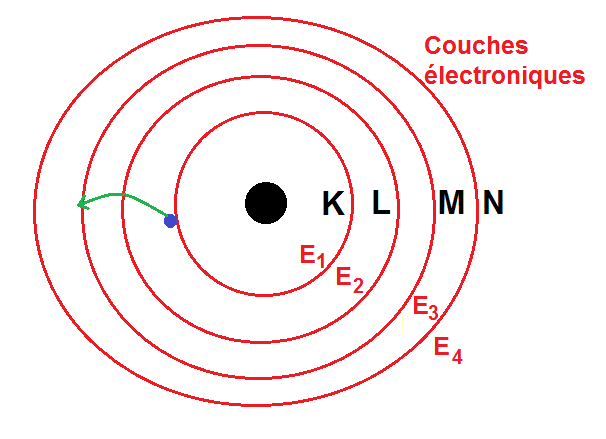
En première approximation, les couches électroniques de l’atome correspondent aux niveaux d’énergie. On a représenté en vert une transition énergétique (l’électron passe d’une couche à l’autre, c’est-à-dire d’un niveau d’énergie à un autre
Si l’électron arrive sur E∞, il ne sera plus sur les couches électroniques : il ne sera donc plus lié à l’atome.
Si en exercices on te demande quelle est l’énergie à fournir à un atome pour devenir un ion, il s’agit de l’énergie pour arriver à 0 eV, mais tout dépend de l’électron que l’on considère.
Si l’électron est au niveau d’énergie -4,8 eV, il faudra donc un photon d’énergie 4,8 eV pour arriver à 0 eV et arracher l’électron à l’atome.
Remarque : normalement il y a des électrons sur chaque couche, donc l’énergie MINIMALE à fournir est celle nécessaire à arracher un électron sur la couche la plus proche de 0 eV.
Passons maintenant aux exemples d’application !
Nous allons voir le type de questions classiques que l’on peut te demander par rapport à ce que l’on a vu dans ce chapitre.
1er exemple : On donne le diagramme d’énergie d’un atome.
Calculer la longueur d’onde de la radiation émise lors du passage d’un électron du niveau E4 au niveau E2.
A quel domaine appartient cette radiation ?
Représenter cette émission sur le diagramme.
On donne la constante de Planck h = 6,63 × 10-34 J.s, la célérité de la lumière dans le vide c = 3,00 × 108 m.s-1 et 1eV = 1,60 × 10-19 J.
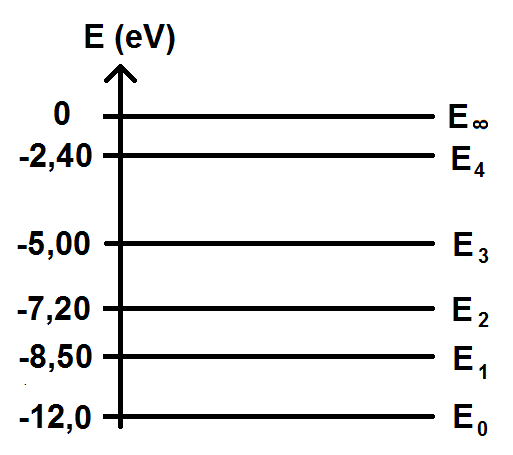
Réponse : lors du passage de l’état 4 à l’état 2, l’atome va se désexciter, il va donc émettre un photon d’énergie :
\(\textstyle \Delta E = |E_4 – E_2| \)
Cette énergie étant celle du photon, on a :
\(\textstyle \Delta E = h\frac{c}{\lambda} \)
D’où :
\(\textstyle |E_4 – E_2| = h\frac{c}{\lambda} \)
\(\textstyle \lambda = h\frac{c}{|E_4 – E_2|} \)
\(\textstyle \lambda = 6,63 \times 10^{-34}\frac{3,00 \times 10^8}{|-2,40 \times 1,60 \times 10^{-19} – (-7,20 \times 1,60 \times 10^{-19})|} \)
ATTENTION à convertir les eV en Joules !!!
\(\textstyle \lambda = 2,59 \times 10^{-7} m \)
Pour que cela soit plus simple on va mettre la longueur d’onde en nm :
\(\textstyle \lambda = 259 nm \)
La longueur d’onde de la radiation émise est donc de 259 nm.
Cette radiation est donc dans le domaine des UV (inférieure à 400 nm).
On peut représenter l’émission de cette radiation sur le diagramme :
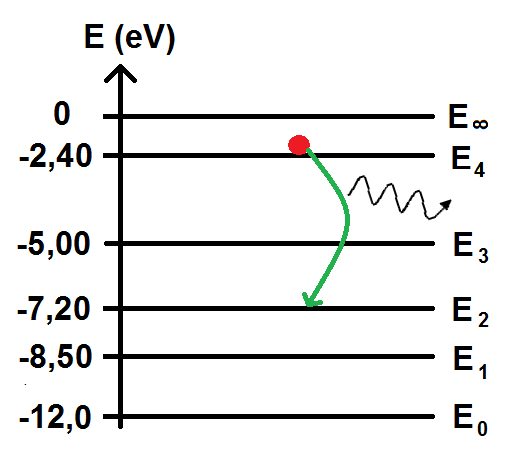
La difficulté principale se situe au niveau du calcul : il ne faut pas oublier de convertir les énergies en Joules dans la formule, pas en eV !!!
De plus, ne pas oublier que la longueur d’onde est en m, mais qu’il est préférable de la mettre en nm pour savoir dans quel domaine elle se situe (visible, infrarouge ou ultra-violet).
2ème exemple : on a toujours le même diagramme.
L’électron est sur le niveau E1. On souhaite qu’il aille sur le niveau E3.
Quel doit être la fréquence de la radiation absorbée par l’atome pour effectuer une telle transition ?
Réponse : pour passer du niveau E1 au niveau E3, l’atome doit absorber un photon ayant une énergie :
\(\textstyle \Delta E = |E_3 – E_1| \)
Cette énergie étant celle du proton, on a :
\(\textstyle \Delta E = hf \)
D’où :
\(\textstyle |E_3 – E_1| = hf \)
\(\textstyle f = \frac{|E_3 – E_1|}{h} \)
\(\textstyle f = \frac{|(-5,00 \times 1,60 \times 10^{-19}) – (-8,50 \times 1,60 \times 10^{-19})|}{6,63 \times 10^{-34}} \)
\(\textstyle f = 8,45 \times 10^{14} Hz \)
La fréquence du photon émis (ou de la radiation émise) est donc f = 8,45 × 1014 Hz.
Comme tu le vois il suffit d’appliquer les formules ! 
Attention toutefois à utiliser la bonne : dans le 1er exemple on cherchait la longueur d’onde donc on a utilisé la formule avec la longueur d’onde, mais dans la 2ème exemple on cherchait la fréquence, on a donc utilisé la formule avec la fréquence (logique !).
Note au passage le respect du nombre de chiffres significatifs (ici le résultat en a 3 puisque chaque donnée de l’énoncé en a 3).
Encore une fois attention à bien convertir les énergies en Joules !!
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !



juste super et merci pour tout!
Merci , je comprends mieux maintenant . Encore merci 🙂
Ce cour est super bien expliqué ! De manière détaillé et simple en plus. Merci beaucoup.
Bonjour, merci pour ce cours très bien expliqué !
J’aurai une question concernant les niveaux d’énergie indiqués: si j’ai bien compris, un électron peut aller de la sous-couche 2s2 à la sous couche 3s2 -par exemple pour l’Aluminium- , on peut avoir la même chose avec le magnésium ( son électron de la sous-couche 2s2 peut passer à la sous couche 3s2) ; du coup pourquoi n’a-t-on pas les niveaux d’énergie pour tous les atomes ayant le même type de déplacement d’un couche vers une autre ?
Bonjour,
Bravo pour ce super cours!
Une question svp:
Les niveaux d’énergies correspondent il aux couches (et/ou sous couches) électroniques de l’atome considéré?
Merci par avance et encore bravo!
Merci ! Oui tout à fait !
Intégralement mon cours mais plus détaillé merci du coup de pouce
Bonjour, je ne comprends pas quelles sont les étapes qui permettent aux photons émis par la lumière solaire arrivant sur la cellule de délivrer un courant électrique, pourriez-vous m’aider ?
Merci
Les photons ont une certaine énergie, la cellule permet de convertir cette énergie en énergie électrique.
Bonjour Monsieur,
Est-ce qu’il existe une méthode facile pour calculer une fréquence intermédiaire si nous connaissons les fréquences extrêmes ?
Peux-tu préciser ta question ?
Merci bcp pour votre aide
Wah ! J’avais un exo à faire, une activité plus précisément, et je n’avais aucun souvenir d’avoir fait une leçon dessus… Donc j’ai cherché sur le net, et je suis tombé sur votre leçon… C’est super clair ! Tout est si bien expliqué, bien structuré… Si bien que lorsque je suis retombé sur ma leçon, je n’en ai définitivement pas eu besoin ! x)
Merci beaucoup !
Merci à toi ! 🙂
Merci, très clair
Bonjour, merci beaucoup pour votre article très intéressant !
Cependant j’ai une question, car il y a un point qui me perturbe :
Vous nous dites qu’à un niveau d’énergie égal à 0 eV l’électron peut se retirer du cortège et l’atome est ionisé. Mais si on assimile le diagramme d’énergie aux différentes couches électroniques KLM, si on suit cette logique, pour que l’atome soit ionisé il faut apporter une énergie suffisante qui fait exclure le dernier électron du cortège…du coup vous nous donnez l’exemple que si un électron se situe sur une couche assez éloigné du noyau, par exemple qu’il est à un niveau de -4,8 et qu’un exercice me demande quel énergie fournir à cet atome pour l’ioniser ; je répondrait 4,8 eV pour que cela donne 0…et vous avez dit que l’énergie minimal à fournir pour ioniser est celle qu’il faudrait pour arracher *l’électron se situant sur un niveau d’énergie le plus proche de 0 eV*
*Mais c’est ça que je ne comprend pas et qui me perturbe….* Car j’ai toujours appris qu’un rayonnement est ionisant seulement si sa longueur d’onde est en dessous de 100 nm (donc si on reproduit le calcul de la dernière fois, ce sera seulement si son énergie est de minimum 12,4 eV).. c’est une famille particulière, mais ce que je comprend pas c’est que si je comprend bien votre logique c’est que tous les rayonnements peuvent être ionisants du coup (si même des rayonnements transportant une énergie de 4,8 eV très inférieure à 12,4 eV peuvent ioniser certains…). Donc tous les rayonnements peuvent-être un peu ionisants ? C’est juste ça que je comprend pas
Sinon merci beaucoup pour votre travail, vous expliquez très bien ! Bonne continuation à vous !
Bien Cordialement
Merci beaucoup !
Oui en effet tous les rayonnements peuvent être ionisants, le 12,4 eV que tu as appris doit être un cas particulier.
Je n’ai pas trop développé car ce n’est pas au programme, mais il existe sur internet des articles plus détaillés sur l’énergie d’ionisation, je t’invite à les lire pour plus de détails 🙂
Bon courage !
Bonjour,
Merci beaucoup pour votre réponse ! Oui je m’étais fini par me trouver une réponse, le jour même (le 12 juin) !
Dans mon cas je pense que, puisque on s’intéresse essentiellement à l’impact sur la matière vivante, l’on définit comme « ionisant » un rayonnement qui transporte une énergie supérieure à l’énergie de liaison des électrons les moins liés des principaux atomes constitutifs du vivant (C,H,N,O etc)..donc serait qualifié de « ionisant » tout rayonnement transportant une énergie de minimum 12,4 eV (Mais cette définition ne veut pas dire qu’un atome se prenant un rayonnement d’énergie inférieure à 12,4 eV ne peut pas être ionisé)
Ce serait du coup une forme de convention venant de l’ionisation des CHON ^^ (en espérant ne pas avoir faux [?]) xD car sinon oui, un peu tous les Rayons pourraient être considérés comme « ionisants » sinon 😅
Encore merci beaucoup 🙏🏻😊
Merci à toi et bon courage ! 🙂
Cours très bien fait et compréhensible. Cependant dans le nouveau programme les couches électroniques ne sont plus abordées de la même manière.
Merci ! Oui je vais faire la nouvelle version bientôt 🙂
Super utile merci beaucoup!
Toutefois, je ne comprends pas dans un exercice menant vers le cours la question : Comment interpréter les radiations émises par une entité chimique à partir de son diagramme énergétique?
Merci ! Les radiations sont émises quand on passe d’un niveau à un autre, et l’énergie de la radiation émise correspond à la différence d’énergie entre les 2 niveaux.
c’est vraiment super géniale.très bien claire,très bien expliqué.un grand merci et chapeau bas.
Bonjour,
Je suis enseignant en BTS et je cherchais un moyen de rendre ce cours accessible et compréhensible à mes élèves et le tout à distance en ces temps d’épidémie.
Vos diagrammes sont très clairs et vos explications très intéressantes. Cela m’a permis de créer un cours bien plus abouti que je ne le pensais et je ne manquerai pas d’envoyer mes élèves vers votre site pour toutes questions complémentaires.
Bonjour, merci beaucoup et bon courage !
Cours très complet, vachement utile pour les cours à distance, merci bcp
Néanmoins il me semble qu’il y a une erreur dans le premier exemple il est écrit que l’électron passe du niveau 4 au niveau 2 donc la formule serait deltaE= E2-E4 or il est écrit deltaE= E4-E2. Ou j’ai peu être mal compris le cours car c’est une notion nouvelle que l’on a pas encore vu en classe juste à distance ^^’
Merci beaucoup ! En fait comme on prend la valeur absolue cela revient au même de faire E2 – E4 ou E4- E2.
Juste génial est hyper clair
très complet et bien expliqué, merci beaucoup!
super utile. Merci !