Sommaire
Exprimer les coordonnées polaires en cartésiennes
Fil qui s’enroule autour d’un cylindre
Pour accéder au cours sur , clique ici !
On considère le schéma suivant :
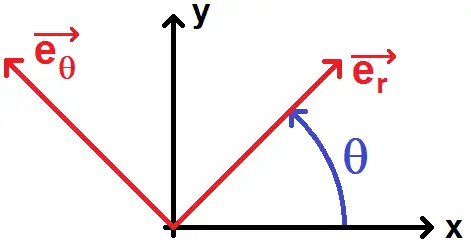
Dans cette vidéo nous allons démontrer les formules vues en cours.
Il s’agit d’exprimer les vecteurs suivants en fonction des vecteur ux et uy :
dans un premier temps :
\(\textstyle \overrightarrow{e_r} \, \, et \, \, \overrightarrow{e_\theta} \)
puis dans un second temps :
\(\textstyle \frac{d\overrightarrow{e_r}}{dt} \, \, et \, \, \frac{d\overrightarrow{e_\theta}}{dt} \)
On considère un cylindre de rayon R et d’axe z. Un fil de longueur l0, de masse négligeable et supposé tendu en permanence est accroché au point A situé sur l’axe (Ox). Initialement le fil est tendu selon y.
A l’autre extrémité du fil se situe un objet ponctuelle M de masse m, lancé avec une vitesse initiale v0 selon le vecteur –ux.
On note B le dernier point qui à l’instant t est entré en contact avec le cylindre.
On note l la longueur du fil qui n’est pas encore enroulée autour du cylindre, c’est-à-dire la longueur BM. On précise que cette longueur est toujours tangente au cylindre.
On note également θ l’angle d’enroulement du fil autour du cylindre.
On considérera les coordonnées polaires dont les vecteurs sont en bleu clair sur le schéma ci-dessous :
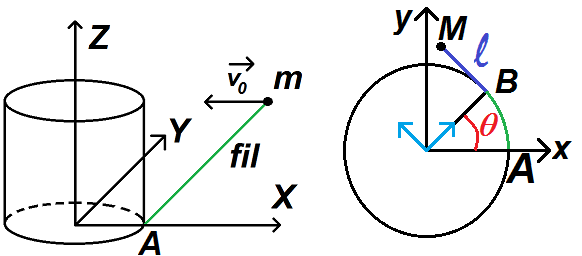
Remarque : les vecteurs seront notés en gras dans les questions.
1) Donner la relation entre l, l0, R et θ.
2) Exprimer le vecteur OM en fonction de l0, R, θ et des vecteurs er et eθ.
3) Exprimer le vecteur v(M)
4) Montrer que la norme ||v|| est constante.
5) En déduire une relation entre θ, dθ/dt, l0, R et v0.
6) En déduire θ(t).
7) A quel temps le fil est-il entièrement enroulé ?
8) Exprimer le vecteur tension T.
Retour au cours Haut de la page


