Sommaire
Introduction
1ère loi de Kepler
2ème loi de Kepler : loi des aires
3ème loi de Kepler
Mouvement circulaire : accélération centripète
Exercices
Ce chapitre s’inscrit dans la continuité du chapitre sur l’attraction gravitationnelle.
En effet, nous y avions parlé de la force existant entre deux planètes.
Dans ce chapitre, nous allons voir les 3 lois de Kepler qui régissent le mouvement des planètes dans l’espace.
Les deux premières lois ne comportent pas de calcul contrairement à la troisième, nous ferons donc des exemples d’application uniquement sur la troisième loi.
Avant de commencer faisons un peu de géométrie, on va en avoir besoin pour la suite !
Une ellipse a la forme suivante (un ballon de rugby), et possède un grand axe et un petit axe.
On peut couper le grand axe en deux parties appelées chacune demi-grand axe :
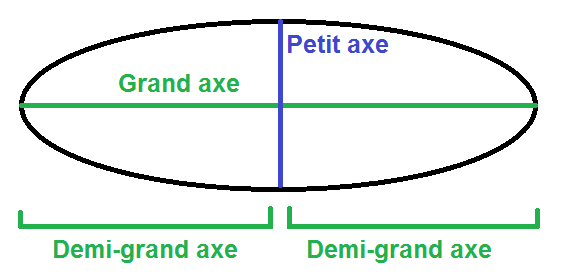
Sur chaque demi-grand axe il existe ce que l’on appelle un foyer.
—
ATTENTION : le foyer n’est pas le centre de l’ellipse !
Le foyer est situé sur le grand axe, mais attention, pas au milieu du demi-grand axe ! Il est plus proche du bord de l’ellipse que du centre.
—
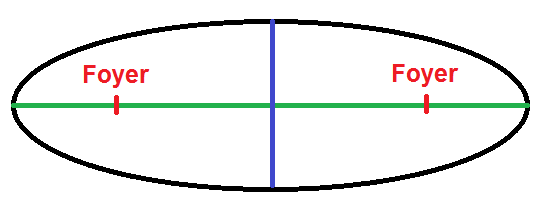
Attention les foyers ne sont pas au centre des demi-grands axes !
Après ce petit préambule, passons au vif du sujet 
L’énoncé de la première loi de Kepler (parfois appelé loi des orbites) est le suivant :
—
Dans le référentiel héliocentrique, les planètes du système solaire décrivent des trajectoires elliptiques, dont le Soleil occupe l’un des foyers.
—
Voyons en détails cette loi :
– le référentiel héliocentrique est le référentiel centré sur le Soleil comme son nom l’indique (hélios = Soleil en grec).
– les planètes du système solaire sont celles qui tournent autour du Soleil (comme la Terre, Mars, Vénus etc…).
– ces planètes décrivent des ellipses autour du Soleil.
– le Soleil est un des foyers de ces ellipses (on a pris le foyer de gauche sur le schéma mais on aurait très bien pu prendre l’autre).
On a alors le schéma suivant :
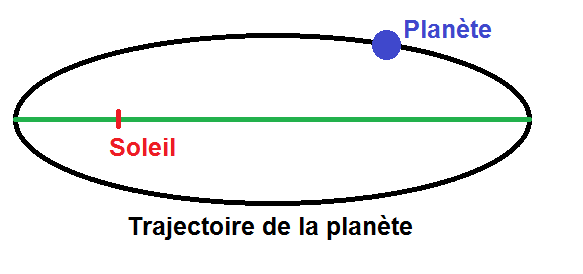
Apprends bien par cœur l’énoncé de la loi car il peut t’être demandé en question de cours.
La deuxième loi de Kepler est aussi appelée loi des aires (tu vas comprendre pourquoi 
)
L’énoncé de cette loi est le suivant :
—
Pendant des durées égales, le segment reliant le Soleil à une planète balaie des aires égales.
—
Il est possible que tu trouves d’autres formulations de cette loi mais cela revient au même^^
L’idée est la suivante : on prend deux positions différentes de la planète sur sa trajectoire. On trace le segment reliant la planète au Soleil.
On regarde l’aire balayée par ce segment pendant le même temps de trajet : ces aires sont égales ! Elles sont notées A1 et A2.
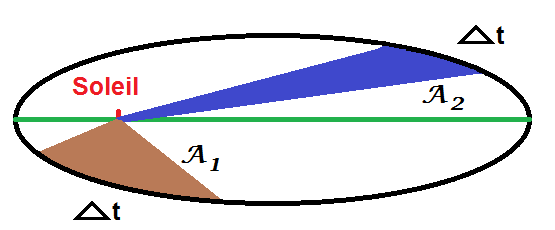
Le Δt signifie que A1 et A2 ont été parcourues pendant le même temps Δt.
La loi des aires nous dit que A1 = A2, tout simplement !
Remarque : le segment reliant la planète et le Soleil est parfois appelé rayon-vecteur (même si ce n’est pas un vecteur…).
La troisième loi de Kepler (parfois appelée loi des périodes) est celle que tu utiliseras le plus en exercice car il y a une formule !
C’est également celle qui, dans son énoncé, fait le plus peur mais ne t’inquiète pas nous allons expliquer tout ça
L’énoncé est le suivant :
—
Le rapport du carré de la période de révolution par le cube du demi-grand axe est constant.
—
Et là tu te dis 
Voyons cela en détails :
La période de révolution, notée T, est le temps mis par la planète pour faire toute la trajectoire. Pour la Terre par exemple, c’est 365 jours. Mais attention, T est en secondes !!!
Donc le carré de la période de révolution est T2.
Le demi-grand axe est la longueur du demi-grand axe (voir schéma tout au début). Il est souvent noté a. Le demi-grand axe est en mètres.
Le cube du demi-grand axe est donc a3.
Le rapport des deux est donc T2/a3.
La troisième de Kepler nous dit que ce rapport est constant :
\(\displaystyle \frac{T^2}{a^3} = constante \)
Cette constante a même une expression :
\(\displaystyle \frac{T^2}{a^3} = \frac{4 \Pi^2}{G \times M_S} \)
Dans cette formule :
G est la constante de gravitation universelle vue dans le chapitre sur l’attraction gravitationnelle (la valeur est toujours donnée dans l’énoncé)
MS est la masse du Soleil, en kg.
Nous verrons la démonstration de cette formule un peu plus bas dans la partie sur les mouvements circulaires.
En réalité, on admet que la 3ème loi de Kepler s’applique également à des mouvements autour de planète autres que le Soleil.
En effet, on peut considérer des planètes qui tournent autour d’une autre planète, Vénus par exemple. Vénus sera alors au foyer des ellipses, ce sera la planète centrale.
Dans la formule, la masse du Soleil sera remplacée par la la masse de Vénus.
—
Retiens donc plutôt la formule :
\(\textstyle \frac{T^2}{a^3} = \frac{4 \Pi^2}{G \times M} \)
M est la masse de la planète centrale, celle autour de qui tournent les autres planètes (ou satellites) que l’on considère.
T et a sont en revanche la période et le demi-grand axe de la planète tournant autour de la planète centrale.
—
Mais à quoi peut bien servir cette formule ??
Deux cas d’application peuvent se présenter.
Le premier assez simple : tu as toutes les données de la formule sauf une, tu calcules alors la donnée inconnue en l’isolant dans la formule.
Par exemple pour la rotation de la Terre autour du Soleil (la planète centrale est donc le Soleil), on donne :
T = 365 jours = 365 × 24 × 3600 = 31536000 s
MS = 2,00 × 1030 kg
G = 6,68 × 10-11 m3.kg-1.s-2
Question : calculer le demi-grand axe de la trajectoire de la Terre autour du Soleil.
D’après la 3ème loi de Kepler :
\(\textstyle \frac{T^2}{a^3} = \frac{4 \Pi^2}{G \times M_S} \)
Il faut isoler le a :
\(\textstyle \frac{T^2 \times G \times M_S}{4 \Pi^2} = a^3 \)
\(\textstyle (\frac{T^2 \times G \times M_S}{4 \Pi^2})^{\frac{1}{3}} = a \)
(on rappelle en effet que pour enlever le cube il faut prendre la racine cubique, c’est-à-dire puissance 1/3…)
Il suffit maintenant de remplacer :
\(\textstyle a = (\frac{31536000^2 \times 6,68 \times 10^{-11} \times 2,00 \times 10^{30}}{4 \Pi^2})^{\frac{1}{3}} \)
\(\textstyle a = 1,50 \times 10^{11} m \)
Soit 150 millions de km. Cela correspond à la distance Terre-Soleil !
Nous verrons dans la partie sur le mouvement circulaire que cela est logique…
Le deuxième type d’application de la formule est un peu différent.
Prenons deux planètes qui tournent autour du Soleil, Mars et Vénus.
La période de Mars est de 687 jours, son demi-grand axe est 228 millions de km.
Pour Vénus on ne connaît que sa période de révolution : 225 jours.
On note TM et aM la période et le demi-grand axe de Mars, TV et aV la période et le demi-grand axe de Vénus.
On cherche le demi-grand axe de la trajectoire de Vénus autour du Soleil.
On suppose que l’on n’a pas la masse du Soleil (sinon on ferait comme au-dessus…).
L’idée est la suivante : Mars et Vénus tournant tous les deux autour du Soleil, leur T2/a3 est le même :
\(\textstyle \frac{T_M ^2}{a_M ^3} = \frac{T_V ^2}{a_V ^3} \)
On isole ce quel’on cherche :
\(\textstyle a_V ^3 = \frac{T_V ^2 \times a_M ^3}{T_M ^2} \)
\(\textstyle a_V = (\frac{T_V ^2 \times a_M ^3}{T_M ^2})^{\frac{1}{3}} \)
Exceptionnellement on peut laisser les périodes en jours et les demi-grand axes en millions de km (car tout cela se compense) :
\(\textstyle a_V = (\frac{225^2 \times 228^3}{687^2})^{\frac{1}{3}} \)
\(\textstyle a_V = 108 \, millions \, de \, km \)
Là encore on trouve un résultat cohérent (la distance entre le Soleil et Vénus est d’environ 108 millions de km).
Comme tu le vois l’application de la formule est très différente, car on utilise le fait que le rapport est constant pour faire une égalité entre deux rapports de deux planètes différentes, sans se soucier de la valeur de la constante.
Dans la première application en revanche on utilisait l’expression de la constante, mais on n’avait besoin que d’une seule planète tournant autour de la planète centrale.
—
ATTENTION cependant !! Pour la deuxième application, il faut que les deux satellites tournent autour de la MÊME planète !
Si tu considères la Lune autour de la Terre et Saturne autour du Soleil, les rapports ne seront pas égaux !
En effet, dans la constante 4Π2/GM, le M est la masse de la Terre dans le 1er cas (car la Lune tourne autour de la Terre) mais le M sera la masse du Soleil dans le 2ème cas (car Saturne tourne autour du Soleil), la constante ne sera donc pas la même donc les rapports ne seront pas égaux…
—
Voyons maintenant un cas particulier que l’on va beaucoup utiliser dans les exercices : le mouvement circulaire uniforme.
En effet, d’après la 1ère loi de Kepler, les planètes ont des trajectoires elliptiques.
Mais si le grand axe et le petit axe de l’ellipse sont égaux, l’ellipse devient… un cercle !
Le cercle est en effet une ellipse particulière, de la même manière qu’un carré est un rectangle particulier.
En contrôle et au bac on considérera presque toujours que les trajectoires sont circulaires car on va pouvoir effectuer des calculs, contrairement aux ellipses…
Le mouvement sera donc circulaire, et sera donc caractérisé par son rayon R.
—
Remarque : puisque le cercle est une ellipse particulière, le rayon correspond… au demi-grand axe !
Donc a = R.
Ainsi, si l’on considère la trajectoire de la Terre autour du Soleil, ce rayon correspond à la distance entre la Terre et le Soleil.
Il est donc logique, dans les exemples vus plus hauts, que le calcul du demi-grand axe de Vénus nous donne la distance entre le Soleil et Vénus…
—
On va préciser encore plus en disant que la vitesse de la planète (ou du satellite) sera constante : le mouvement est dit uniforme.
On va donc considérer des mouvements circulaires uniformes :
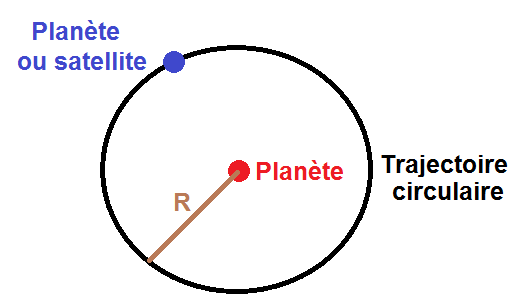
Pour ce genre de mouvements (circulaires ET uniformes), on dit que l’accélération est centripète, c’est-à-dire qu’elle est dirigée vers le centre de la trajectoire (là où se situe la planète centrale) :
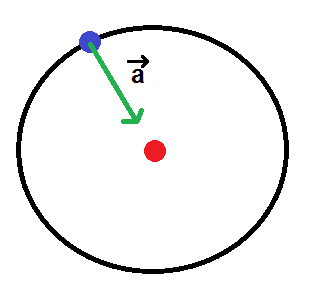
Pour un mouvement circulaire uniforme, l’accélération est centripète (dirigée vers le centre)
—
ATTENTION ! Désormais le a n’est plus le demi-grand axe mais l’accélération… oui c’est un piège 
—
Toujours dans le cas des mouvements circulaires uniformes, la norme de cette accélération a même une formule !
\(\displaystyle a = \frac{v^2}{R} \)
—
ATTENTION ! Dans cette formule le a correspond à l’accélération et non au demi-grand axe vu plus haut…
—
Dans cette formule :
a est l’accélération en m.s-2
v est la vitesse en m.s-1
R est le rayon de la trajectoir en en m. Ce rayon correspond à la distance entre les deux planètes.
—
ATTENTION ! Cette distance est souvent donnée en km voire en millions de km comme dans les exemples vus précédemment.
Pense donc bien à convertir en mètres…
—
Remarque : comme on l’avait vu dans le chapitre sur la gravitation, il est possible que le rayon de la trajectoire corresponde à R + h, c’est-à-dire le rayon de la planète centrale + l’altitude de l’objet (souvent un satellite) :
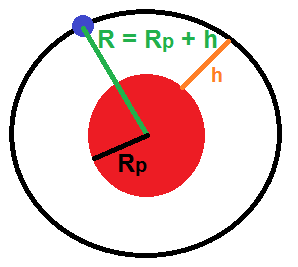
Le rayon de trajectoire correspond au rayon de la planète centrale (Rp) + l’altitude (h)
Comme promis ci-dessus, voyons la démonstration permettant de prouver la 3ème loi de Kepler et de trouver la constante .
Prenons une planète de masse m ayant une trajectoire circulaire uniforme (vitesse v, rayon R) autour d’une autre planète de masse M.
D’après la deuxième loi de Newton (en prenant la norme, donc sans les vecteurs), la seule force étant la force d’attraction entre les planètes, on a :
\(\textstyle m \times a = G \frac{m \times M}{R^2} \)
On simplifie par m :
\(\textstyle a = G \frac{M}{R^2} \)
Le mouvement étant circulaire uniforme, on a vu que a = v2/R :
\(\textstyle \frac{v^2}{R} = G \frac{M}{R^2} \)
En simplifiant les R :
\(\textstyle v^2 = G \frac{M}{R} \)
Le mouvement étant uniforme, on peut appliquer la formule v = d/t.
Si l’on prend comme temps la période de révolution T, d correspondra à la distance parcourue pendant une période, c’est-à-dire une trajectoire complète, donc le périmètre du cercle ! Donc on a d = 2πR :
\(\textstyle (\frac{2 \Pi R}{T})^2 = G \frac{M}{R} \)
\(\textstyle \frac{4 \Pi^2 R^2}{T^2} = G \frac{M}{R} \)
\(\textstyle \frac{4 \Pi^2}{G \times M} = \frac{T^2}{R^3} \)
Et voilà, on vient de démontrer la formule de la 3ème loi de Kepler !
Et le M correspond à la masse de la planète CENTRALE. 4Π2/GM est donc une constante qui est la même pour toutes les planètes tournant autour de cette planète.
Cette démonstration peut t’être demandée au contrôle donc apprends la bien, de même que l’énoncé des 3 lois !
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !
Bonjour,
En pratique, y a t il des exercices ou des problèmes dont la résolution utilise la 2e loi de Kepler au niveau terminale ? Cela ne semble pas évident à imaginer.
Merci pour votre cours
Oui mais c’est assez rare.
Bonjour,
dans votre partie sur les applications de la 3ème loi de Kepler, vous écrivez: « ATTENTION cependant !! Pour la deuxième application, il faut que les deux planètes tournent autour de la MÊME planète ! »
Ça fait beaucoup de planètes qui se tournent autour. Je pense qu’il manque une étoile à l’affaire.
Bonne soirée,
David
En effet, j’aurais pu dire que les deux satellites tournent autour de la même planète, je vais modifier cela.
Merci !
Salut,
Je pense que ce n’est pas à cause de G que la formule ne s’applique pas à deux planètes qui ne. Tournent pas sur une même troisième. G est universelle. C’est plutôt que les masses m ne seront pas les mêmes et donc on pourra pas simplifier m dans la démonstration. J’apprécie beaucoup votre cours.merci