Sommaire
Équations de Maxwell et équation de propagation
Équations de Maxwell dans l’ARQS
Potentiel créé par un dipôle
Charges dans un triangle équilatéral
Charges aux sommets d’un carré
Champ électrique créé par un plan infini
Condensateur avec 2 plans chargés
Champ magnétique créé par une spire
Champ magnétique créé par un fil fini
Champ créé par un solénoïde infini
Champ créé par un solénoïde fini
Champ créé par un cylindre infini
Champ magnétique créé par une nappe de couranti
Champ magnétique créé par un tore
Le rail de Laplace
Spire dans un champ magnétique
L’effet de peau
Champ tournant avec 3 bobines
Moteur synchrone et champ tournant
Moteur asynchrone et champ tournant
Densité volumique de charge variable
Condensateur sphérique
Champ dans une cavité sphérique
Modèle de Drude
Mouvement hélicoïdal dans un champ magnétique
Rappeler les équations de Maxwell et trouver les équations de propagation des champs B et E dans le vide.
On considère un métal de conductivité γ = 106 Ω-1.m-1
On rappelle que ε0 = 8,85 x 10-12 S.I.
1) Démontrer l’équation locale de conservation de la charge
2) Montrer que l’on peut considérer que ρ = 0
3) Simplifier les équations de Maxwell si f = 25 kHz
On considère un dipôle constitué d’une charge -q et d’une charge q situés aux points A et B d’abscisse -a et a comme sur la figure ci-dessous.
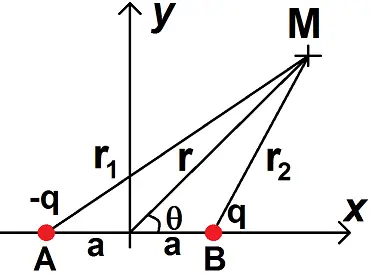
On note OM = r, BM = r2 et AM = r1.
On note θ l’argument de M.
Déterminer le potentiel créé par ce dipôle en un point M très éloigné du dipôle en fonction du moment dipolaire p.
On considère un triangle équilatéral ABC de côté a. On place une charge q à chaque sommet. On note O le centre du triangle.
1) Calculer le champ électrique en A.
2) Calculer le champ électrique en O.
3) On ajoute une charge q0 au point O. Donner la valeur de q0 pour que les différentes forces se compensent.
Même exercice que précédemment mais cette fois-ci avec un carré.
On considère un carré ABCD de centre O et de côté a. On place une charge q > 0 à chacun des sommets.
1) Quel est le champ électrique en O ?
2) Quel est le champ électrique en A ?
3) On ajoute une charge q0 au point O. Donner la valeur de q0 pour que les différentes forces se compensent.
On considère un plan (x ; y) infini uniformément chargé de densité de charge surfacique σ.
Déterminer le champ électrique E créé par ce plan.
On considère 2 plaques de surface S espacées d’une distance d, chargés avec des densités surfaciques de charge σ et -σ.
La plaque chargée σ a un potentiel V1 et la plaque chargée -σ a un potentiel V2, créant une différence de potentiel U.
On obtient le schéma suivant :
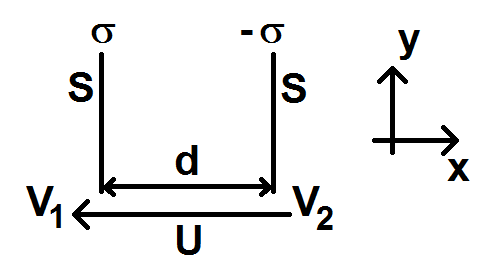
Déterminer la capacité C du condensateur. On considérera que d est négligeable devant les dimensions des plaques.
On considère une spire d’axe (Oz) et de rayon R parcourue par un courant i.
Calculer le champ magnétique créé par la spire en un point M de l’axe (Oz) repéré comme ci-dessous :
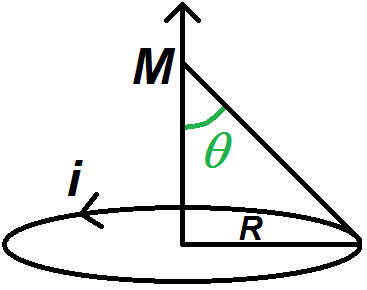
On considère un fil fini de longueur L selon l’axe (Oz), portant une densité linéique de charge λ et de centre O.
On considère un point M situé à une distance r de O tel que (OM) perpendiculaire au fil.
Calculer le champ électrique E au point M
On considère un solénoïde infini d’axe (Oz) constitué de n spires par unité de longueur.
Calculer le champ magnétique créé par ce solénoïde.
On considère un solénoïde fini d’axe (Oz) de longueur L et constitué de N spires.
Calculer le champ magnétique créé par ce solénoïde en un point M de l’axe (Oz) repéré comme ci-dessous :
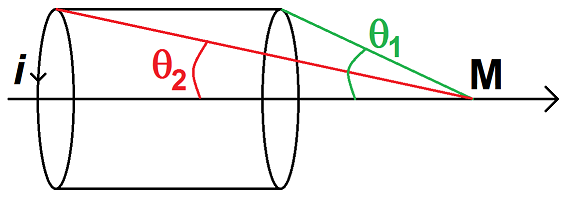
On considère un cylindre infini infini de rayon R parcouru par un courant de densité volumique j.
Déterminer le champ magnétique créé par ce courant.
On considère un plan infini selon le plan (Oxy) parcouru par un courant de densité surfacique j selon les y croissants.
Déterminer le champ B créé par cette nappe de courant.
On considère un tore constitué de N spires parcourues par un courant i comme représenté dans le schéma ci-dessous :
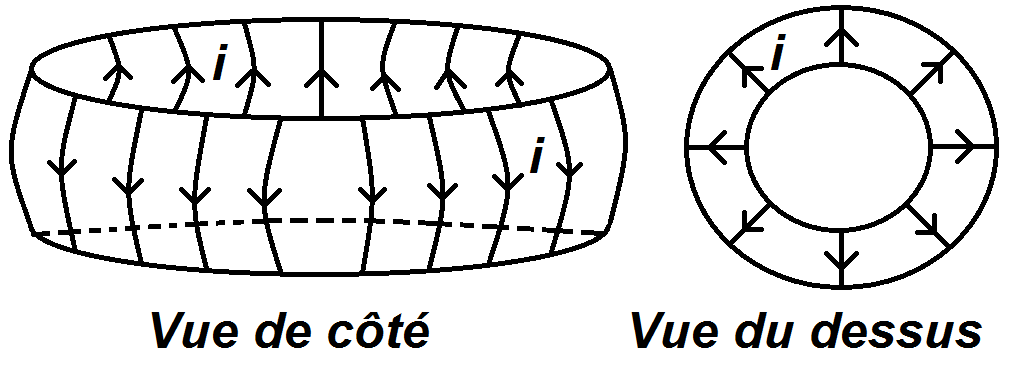
Déterminer le champ magnétique créé par ce tore.
Cet exercice aborde le rail de Laplace, exercice très classique en induction.
On considère le schéma suivant :
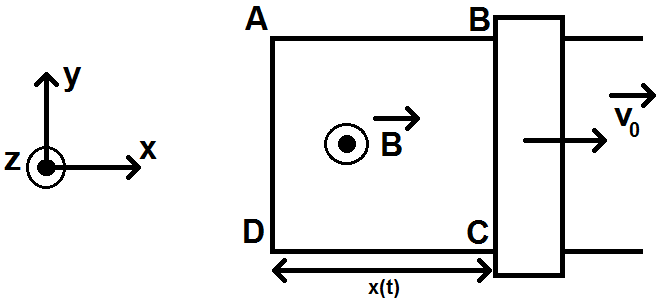
On a un circuit fermé par un rail BC qui coulisse selon l’axe (Ox).
Un champ magnétique B dirigé selon l’axe (Oz) traverse la portion ABCD du circuit.
A t = 0, on lance le rail avec une vitesse V0 dans le sens des x croissants.
On note x(t) la distance DC.
1) Comment évolue la vitesse v(t) du rail ?
2) Etudier l’aspect énergétique du système (on pourra chercher sous quelle forme est dissipée l’énergie initiale).
Dans cet exercice, on considère une spire carrée de côté a et de masse m, d’inductance L et de résistance R.
Dans le demi-plan x > 0, on considère un champ magnétique B dirigé selon (Oz).
A t = 0, la spire entre dans le demi-plan x > 0 avec une vitesse v0 :
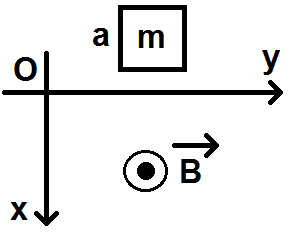
1) On néglige d’abord l’inductance L de la spire.
Trouver l’expression de la vitesse v(t) de la spire.
Donner l’expression de la vitesse limite v∞ atteinte par la spire.
2) On néglige maintenant la résistance R de la spire.
Trouver l’expression de la vitesse v(t) de la spire.
Quelle est la condition pour obtenir des oscillations ?
On considère un métal de conductivité γ pour x ≥ 0
On suppose que :
\(\displaystyle \overrightarrow{\underline{E}} = \underline{E} \, e^{j \omega t} \, \overrightarrow{u_z} \)
Trouver E, puis le vecteur E puis l’épausseur de peau δ.
On pourra utiliser les équations de Maxwell dans le cadre de l’ARQS (voir vidéo en haut de cette page).
Remarque : cet exercice est une question préliminaire pour les 2 exercices suivants sur les moteurs synchrones et asynshcrones.
On considère 3 bobines parcourues par 3 courants de même pulsation ω, de même intensité I0 mais déphasés de 120° l’un par rapport à l’autre, et disposés selon la figure ci-dessous :
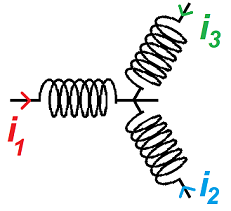
Calculer le champ magnétique B total ainsi créé.
On considère 3 bobines comme étudié dans la vidéo de l’exercice précédent.
On reprendra l’expression du champ B trouvée dans la vidéo précédente.
On ajoute un aimant en rotation autour de l’axe (Oz), de moment dipolaire magnétique M, et faisant un angle ω’t – θ0 avec l’axe (Ox).
1) Calculer le couple associé à ce dipôle puis sa moyenne temporelle.
2) En déduire une condition sur ω’ et justifier l’appellation de moteur synchrone.
3) Y’a-t-il une condition sur θ0 ?
Dans cet exercice on reprendra l’expression de B trouvée dans la vidéo sur le champ tournant créé par 3 bobines car on considère là encore 3 bobines dans la même disposition.
On ajoute au centre une bobine de N spires, de surface S, de résistance R, de vecteur normal n et faisant un angle ω’t avec l’axe (Ox).
On admet que le moment magnétique a pour expression :
\(\textstyle \vec{M} = NSI \vec{n} \)
1) Calculer le couple associé à ce dipôle puis sa moyenne temporelle.
2) En déduire une condition sur ω’ et justifier l’appellation de moteur asynchrone.
Soit b une constante positive.
Calculer le champ électrique créé par une sphère de centre O et de rayon R, dont la densité volumique de charge est :
\(\textstyle \rho = \frac{b}{r}, \, avec \, 0 \lt r \lt R \)
On considère un condensateur sphérique constitué de 2 sphères concentriques de rayon R1 et R2 possédant dans densité surfaciques de charge σ1 et σ2.
Quelle est la condition pour que la charge totale soit nulle ?
Dans ce cas, déterminer le champ électrique E créé par ces 2 sphéères.
On considère une sphère chargée de rayon R et de densité volumique de charge ρ, présentant une cavité sphérique de rayon a située à une distance d du centre.
Calculer le champ électrique à l’intérieur de la cavité.
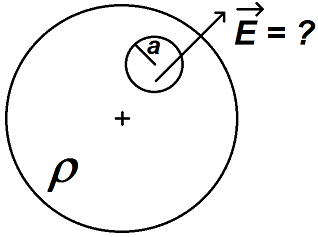
Remarque : les vecteurs sont marqués en gras.
On considère un métal comme un réseau d’ions positifs fixes entourés d’électrons de conduction se déplaçant librement, la densité des électrons étant notée n.
On considère une force de frottement – α v, v étant le vecteur vitesse moyen des électrons sous l’action d’un champ E.
1) Retrouver la loi d’ohm locale après avoir trouvé l’expression du vecteur v.
2) On considère par la suite (2ème vidéo) un champ magnétique en plus. Le champ électromagnétique est :
\(\displaystyle \vec{E}\begin{pmatrix} E_x \\ E_y \\ 0 \end{pmatrix} \, et \, \vec{B}\begin{pmatrix} 0 \\ 0 \\ B \end{pmatrix} \)
Retrouver la relation entre jx, jy, Ex et Ey sous forme matricielle en régime stationnaire.
On considère une particule chargée de charge q initialement à l’origine du repère.
Le vecteur vitesse est (v0, 0, v0z)
Le champ magnétique B0 est constant, de direction verticale selon z, dirigé vers le haut.
Déterminer le mouvement de la particule. On étudiera le cas où q > 0 et q < 0.
Sommaire des exercicesHaut de la page


