Sommaire
Introduction
Bits et octets
Signal numérique et analogique
Échantillonnage
Débit binaire
L’image numérique
Exercices
Ce cours est assez différent des autres chapitres car il fait intervenir des notions qui ne sont pas forcément en lien avec d’autres chapitres.
Avant de commencer le chapitre en lui-même, nous allons parler de bits et d’octets.
Tu as sûrement déjà entendu parlé des octets.
Par exemple dans l’explorateur Windows, tu peux voir la chose suivante :

On voit qu’il y a plusieurs disques durs, et sur celui de gauche par exemple il y a marqué :
48,6 Go libres sur 264 Go
(Go signifie Gigaoctets)
Dans le disque dur il peut y avoir des musiques par exemple, qui sont composées d’un certain nombre d’octets :

Ce fichier de musique par exemple est composé de 5,87 Mo (mégaoctets).
Mais que signifie octets, mégaoctets, gigaoctets, etc… ?
1 octet correspond à 8 bits :
\(\displaystyle 8 \, bits = 1 \, octet \)
Pour ne pas inverser (en disant 8 octets = 1 bit, ce qui est faux…), il est facile de retenir que oct- est le préfixe pour huit (1 octogone par exemple). Ainsi 8 octets signifierait 8 fois 8, ce qui ici n’a pas de sens…
D’accord, mais qu’est-ce-qu’un bit ??
Un bit est l’unité élémentaire en informatique qui peut valoir 0 ou 1.
Toute l’informatique est basée là-dessus.
L’explication du binaire est disponible sur cette page, ce n’est pas indispensable au chapitre mais c’est mieux, ne serait-ce que pour ta culture ! 
Un octet étant composé de 8 bits, 01100101 est un octet, tout comme 11010100 par exemple.
Octets et bits peuvent s’exprimer avec les préfixes kilo, méga et giga :
kbits et ko (kilobits et kilooctets) : x 103
Mbits et Mo (mégabits et mégaoctets) : x 106
Gbits et Go (gigabits et gigaoctets) : x 109
Ainsi 5 Mo correspond à 5 x 106 octets, soit 5 x 106 x 8 = 40 x 106 bits.
Donc un fichier de 5 Mo correspond à 40 millions de bits. Cela peut paraître beaucoup mais pour la technologie actuelle ce n’est pas grand chose…
Il faut cependant faire très attention car il y a d’autres unités qui ressemblent fortement.
kio : kibioctet : x 210
Mio : mébioctet : x 220
Gio : gibioctet : x 230
Comme tu le vois cela ressemble beaucoup au niveau de la notation (on rajoute un i avant le o) mais ce n’est pas pareil !
En réalité, ce n’est pas si éloigné que ça.
En effet : 210 = 1024 ≈ 103
220 = 1048576 ≈ 106
230 = 1073741824 ≈ 109
Bon pour 230 on est un peu loin du compte mais pour 210 et 220 c’est assez proche.
Ainsi, il arrive parfois que l’on fasse l’approximation :
1 ko ≈ 1 kio
1 Mo ≈ 1 Mio
Cependant, ce n’est pas à toi normalement de décider si on fait cette approximation ou non, ce sera dit dans l’énoncé.
D’ailleurs, tu n’as pas à connaître non plus le fait que kio corresponde à 210, et que Mio et Gio correspondent à 220 et 230 : ce sera toujours donné dans l’énoncé (en tout cas au Bac).
On peut donc résumé tout cela à l’aide des tableau suivants :

Dernière chose avant de passer à la suite : avec n bits, on peut compter jusqu’à 2n – 1.
Cela est lié aux vidéos disponibles sur la page déjà donnée au-dessus donc nous ne détaillerons pas le pourquoi du comment, retiens juste qu’avec n bits, on peut compter de 0 à 2n – 1, ce qui fait 2n valeurs.
Ainsi, avec 4 bits, on peut compter de 0 à 24 – 1 = 15, et donc faire 16 valeurs différentes possibles.
—
ATTENTION à ne pas inverser 2n – 1 et 2n !
Avec n bits, on peut compter jusqu’à 2n – 1, mais comme on part de 0, il y a 2n valeurs différentes.
—
Au Bac Amérique du sud 2013 par exemple, il y avait la question :
Combien de valeurs peut prendre un échantillon numérisé sur 8 bits ?
Il fallait alors répondre 28 = 256.
Mais on compte de 0 à 255 (ce n’était pas demandé dans l’énoncé mais il faut bien l’avoir en tête).
Retiens bien cet exemple car on s’en servira beaucoup par la suite, puisque 8 bits = 1 octet 
Rentrons maintenant dans le chapitre à proprement parlé : commençons par voir la différence entre un signal numérique et un signal analogique.
Graphiquement cela se traduit de la manière suivante :
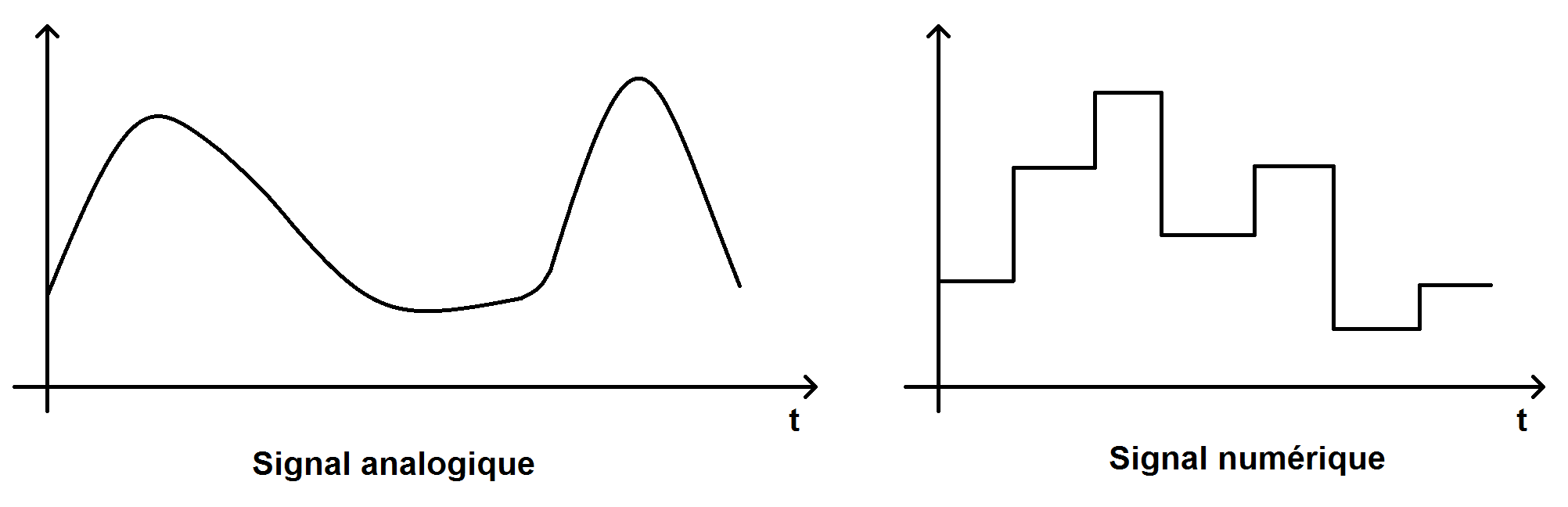
Le signal analogique, à gauche, varie de manière continue, il peut prendre n’importe quelle valeur en ordonnée.
Le signal numérique varie quant à lui de manière discontinue, et ne peut prendre que certaines valeurs discrètes.
Remarque : il s’agit de la même différence en mathématiques entre les lois discrètes et les lois continues en probabilités.
On peut ainsi retenir les définitions suivantes :
—
Un signal analogique varie de façon continue au cours du temps.
Un signal numérique varie de manière discrète au cours du temps.
—
Retiens bien ces définitions car elles sont souvent demandées en question de cours, et presque à chaque fois au Bac !!
Mais quelle est l’utilité de connaître cette différence ?
Prenons un exemple : imaginons que tu veuilles enregistrer ta voix sur ton téléphone et que tu veuilles envoyer le fichier à un ami sur son téléphone.
Pour cela tu vas parler : tu vas émettre des sons, autrement dit des ondes, qui sont un signal analogique.
Ton téléphone va transformer ce signal analogique en signal numérique pour pouvoir l’envoyer. Pour cela, il faut ce que l’on appelle un CAN : un Convertisseur Analogique – Numérique.
Ce signal numérique va être envoyé sur le téléphone de ton ami. Ce téléphone va retransformer ce signal numérique en signal analogique (en sons) afin que ton ami puisse l’écouter. Pour cela, il va utiliser… un CNA : Convertisseur Numérique-Analogique.
Mais pourquoi convertir en numérique si c’est pour après le reconvertir en analogique ??
Tout simplement parce qu’il est beaucoup plus facile de stocker, transmettre, modifier etc… un signal sous forme numérique que sous forme analogique.
Le signal numérique sera composé de bits (qui valent 0 ou 1), le nombre total de bits fournira la taille du fichier.
On parlera parfois en octets et non en bits.
Nous allons étudier en détails la conversion analogique-numérique (autrement dit le CAN).
Il s’agit donc de transformer le signal analogique en signal numérique.
Remarque : le signal analogique sera toujours en volts en ordonnée (c’est-à-dire une tension). Si jamais le signal initial n’est pas en volts, un appareil se chargera de convertir le signal en une tension. Par exemple un micro sert à convertir le son (une onde) en un signal analogique ayant la tension en ordonnée.
Le problème est que le signal analogique est continu, il comporte donc une infinité de points au cours du temps, mais on ne peut don pas tous les prendre.
De plus, comme on l’a dit précédemment, le signal analogique peut prendre une infinité de valeurs contrairement au signal numérique !
Le premier problème sera résolu avec ce que l’on appelle l’échantillonnage.
—
Échantillonner, c’est prélever des points du signal à intervalles de temps réguliers.
—
Retiens bien cette définition car elle est souvent demandée au contrôle et au Bac !
Autrement dit, si une musique dure 3 minutes par exemple, on ne prendra que 1 point toutes les millisecondes par exemple.
Graphiquement cela donne ça :
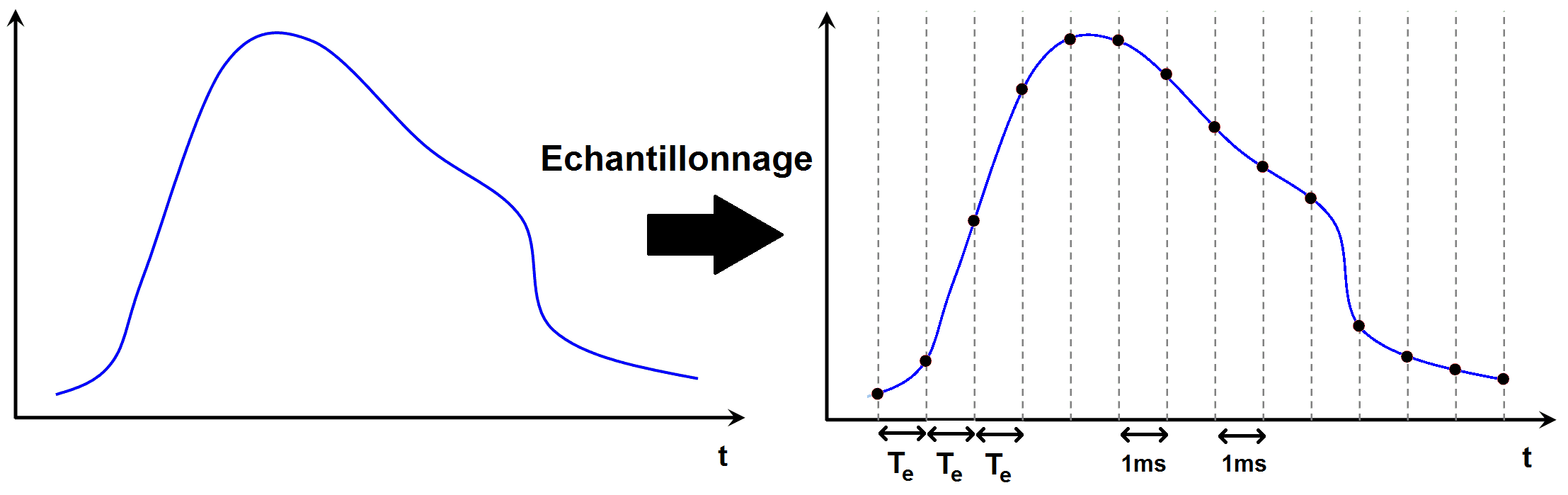
La durée entre deux valeurs échantillonnées est ce que l’on appelle la période d’échantillonnage., notée Te et visible sur le graphe précédent.
Dans cet exemple Te = 1 ms puisque l’on prend 1 point toutes les millisecondes
A cette période on peut associer une fréquence, appelée fréquence d’échantillonnage, notée fe, selon la formule vue dans le chapitre sur les ondes :
\(\displaystyle f_e = \frac{1}{T_e} \)
\(\displaystyle T_e = \frac{1}{f_e} \)
Le premier problème est réglé 
Il faut désormais attribuer à chacun de ces points une valeur discrète du signal numérique.
Pour cela il faut déjà définir quelles sont ces valeurs discrètes.
Les valeurs discrètes du signal numérique seront régulièrement espacées entre la valeur minimale et la valeur maximale du signal analogique.
L’intervalle entre deux valeurs discrètes est appelé le pas du convertisseur, noté p.
Imaginons que l’on ait un signal analogique compris entre 5 V et 17 V.
Ce qu’on appelle la plage, c’est la différence entre ces deux valeurs extrêmes : plage = 17 – 5 = 12 V.
Remarque : la plage est en volts car il s’agit d’une différence de volts.
Ensuite, il faut connaître le nombre de bits du convertisseur : on te dira dans l’énoncé « on a un CAN 8 bits », ou « on considère un CAN 16 bits » etc…
Ce nombre de bits du CAN est noté n.
Ce n correspond au nombre de bits sur lesquels seront codés chaque point échantillonné : chaque point sera représenté par n bits dans le fichier final.
Or on a vu précédemment qu’avec n bits on pouvait faire 2n valeurs différentes.
On a donc la formule :
\(\displaystyle p = \frac{plage}{2^n} \)
La plage étant en volts et le 2n étant sans unité, le pas est en volts.
Si l’on reprend l’exemple du signal dont le plage est de 12 V, et que l’on prend un convertisseur 4 bits, on a :
\(\textstyle p = \frac{12}{2^4} \)
\(\textstyle p = 0,75 \)
Ainsi, les différentes valeurs discrètes du signal numérique partiront de 5 (la valeur minimale) puis progresseront de 0,75 en 0,75 jusqu’à la valeur maximale de 17 :
5 – 5,75 – 6,5 – 7,25 – 8 – 8,75 – 9,5 – 10,25 – 11 – … – 17
Si un des points de l’échantillonnage a pour pour valeur 6,7 V, il aura pour valeur discrète dans le signal numérique la valeur la plus proche, à savoir 6,5 V dans notre exemple.
Ainsi n’importe quelle valeur du signal analogique aura une valeur discrète dans le signal numérique : le deuxième problème est résolu ! 
Graphiquement on obtient cela :
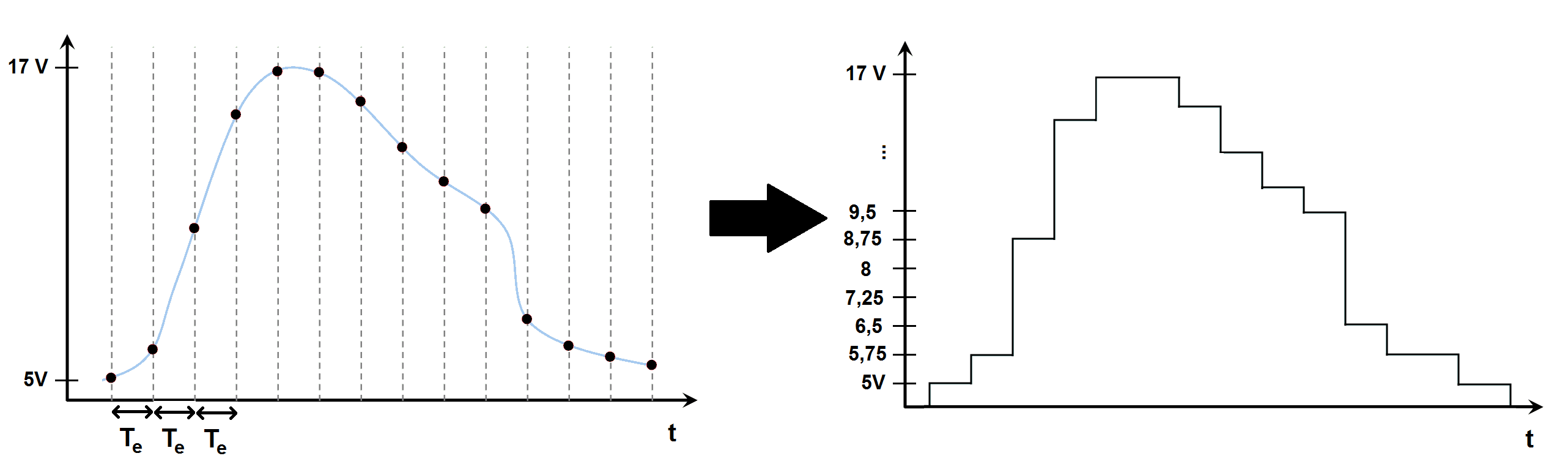
Le signal analogique est désormais numérisé. Mais à partir de ce signal numérique il va falloir reproduire le signal analogique. Pour cela il faut que le numérique corresponde au maximum au signal analogique.
Pour avoir une bonne qualité, il faut beaucoup de points et que ces points soient le plus précis possible.
Il faut donc un petit Te (ou un grand fe), et un grand n pour avoir une qualité maximale.
Le problème est que cela implique que le fichier final aura un grand nombre de bits, ce qui n’est pas forcément idéal…
Si en effet il faut 1 DVD ou 1 Blu-Ray entier pour stocker une seule chanson, ça ne va pas être très rentable… 
Il faut donc trouver le bon compromis entre la période d’échantillonnage et le pas du convertisseur pour obtenir le résultat souhaité.
Le signal numérique, stocké sous forme de fichier sur ton ordinateur par exemple, peut parfois être envoyé sur un autre support (tu envoies une musique à un ami par exemple). Ce fichier est constitué de bits comme on l’a dit précédemment.
Le fichier va être envoyé plus ou moins vite suivant ce que l’on appelle le débit binaire, souvent noté D.
—
Le débit binaire, correspond au nombre de bits envoyés par unité de temps.
—
D’après cette définition, la formule du débit binaire est :
\(\displaystyle D = \frac{n}{t} \)
n correspond au nombre de bits
t correspond au temps mis pour envoyer ces n bits.
D est donc en bit.s-1
D correspond à la vitesse de transmission du signal numérique : plus D est grand, plus le signal est transmis rapidement.
Nous allons maintenant nous intéresser spécifiquement aux images numériques, comme les photos qui sont sur ton téléphone par exemple.
Cette image est composée de pixels qui sont des petits carrés colorés.
Par exemple :
![]()
Une image numérique est composée de petits carrés appelés pixels
Tu auras évidemment reconnu Mario, mais comme il y a peu de pixels ce n’est pas très joli.
Pour avoir une meilleure qualité il faut plus de pixels.
—
Le nombre total de pixels constituant l’image est appelé la définition de l’image.
Elle peut également s’exprimer en octets.
—
Pour calculer cette définition, il faut multiplier le nombre de pixels sur la largeur de l’image par le nombre de pixels sur la longueur de l’image.
Si on a une image de 20 pixels par 30 pixels, la définition de l’image est 30 x 20 = 600 pixels.
Pour l’image de Mario ci-dessus, si l’on fait un quadrillage correspondant aux pixels on obtient ça :
![]()
On voit qu’il y a 16 pixels en horizontal et 14 en vertical, donc une définition de 16 x 14 = 224 pixels.
Chacun de ces pixels va être codé sur un certain nombre de bits.
Si on multiplie le nombre total de pixels par le nombre de bits par pixels, on obtient le nombre total de bits de l’image : c’est ce qu’on appelle la taille de l’image. Ce nombre peut se mettre en bits ou en octets.
—
La taille de l’image correspond au nombre de bits (ou d’octets) total de l’image.
Elle s’obtient en multipliant le nombre de bits par pixels par le nombre de pixels, c’est-à-dire la définition de l’image.
taille = définition x nombre de bits par pixels (si on l’exprime en bits)
taille = définition x nombre d’octets par pixels (si on l’exprime en octets)
—
—
ATTENTION à ne pas confondre la taille et la définition de l’image.
La définition correspond au nombre de pixels de l’image.
La taille correspond au nombre de bits (ou d’octets) de l’image.
—
Il existe deux grands types d’images :
– les images en couleur
– les images en noir et blanc
Pour les images en couleurs, chaque pixel aura une couleur.
Cette couleur sera obtenue en mélangeant les 3 couleurs primaires : Rouge, Vert et Bleu (voir le chapitre sur les couleurs pour plus de détails).
On dit à ce moment-là que l’on est en codage RVB (R pour rouge, V pour vert et B pour bleu).
On peut trouver aussi RGB en Anglais (Red, Green, Blue).
Chaque couleur sera codée sur 8 bits, ce qui donne 3 x 8 = 24 bits pour 1 pixel, soit 3 octets.
—
En codage RVB, chaque pixel est codé sur 24 bits, soit 3 octets.
—
Le rouge, le vert et le bleu sont parfois appelés sous-pixels : chaque pixel est donc composé de 3 sous-pixels, codé chacun sur 8 bits.
On a vu au début du chapitre qu’avec 24 bits, on peut avoir 224 = 16 777 216 valeurs.
Il y a donc plus de 16 millions de couleurs possibles avec ce type de codage !!!
Mais attention, chaque sous-pixel est codé sur 8 bits, ce qui fait 28 = 256 valeurs.
Chaque couleur peut donc prendre une valeur entre 0 et 255 (et non pas entre 0 et 256 ou entre 1 et 256 comme on l’a dit au début du chapitre).
Chaque sous-pixel aura donc une valeur comprise entre 0 et 255.
—
La valeur 0 correspond à une absence totale de couleur, la valeur 255 correspond à l’inverse à une présence maximale de cette couleur.
—
On peut alors trouver la représentation suivante pour un pixel :
![]()
Dans le pixel de gauche, le sous-pixel rouge a pour valeur 125, le vert 43 et le bleu 75.
Grâce à des applications comme Paint, tu peux savoir de quelle couleur il s’agit :
![]()
On voit qu’il s’agit d’une couleur violette.
On a dit précédemment que 0 correspondait à une absence totale de couleur, et 255 à une présence maximale de cette couleur.
On peut donc assez facilement trouver certaines couleurs particulières :
– pour les couleurs primaires comme le rouge par exemple, il suffit de mette uniquement du rouge (R : 255) et ni de vert ni de bleu (V : 0 et B : 0)
– pour le blanc, il faut toutes les couleurs à 255
– pour le noir il faut mettre toutes les couleurs à 0
– pour les couleurs secondaires, qui sont un mélange de 2 couleurs primaires, il faut mettre ces 2 couleurs à 255 et la 3ème à 0.
Pour le cyan par exemple, celui-ci étant du vert et du bleu, on met V : 255 et B : 255, et R : 0.
![]()
Retiens-bien toute cela car au contrôle tu vas sûrement en avoir besoin !!
Pour les images en noir et blanc, c’est un peu le même principe sauf que chaque sous-pixel aura la même valeur.
C’est ce que l’on appelle des niveaux de gris.
Ainsi, en noir et blanc, chaque pixel sera de la forme :
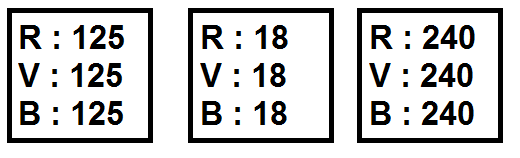
On aura donc 0-0-0 ou 1-1-1 ou 2-2-2 etc… 255-255-255.
Il n’y a donc que 256 niveaux de gris différents, contrairement aux 16 millions de couleurs !!
Mais du coup, à quoi cela sert de répéter 3 fois la même valeur ??
A rien !
Ce pourquoi souvent les images en noir et blanc ne sont pas codés sur 3 sous-pixels mais sur… 1 seul !
Chaque pixel ne sera donc plus codé sur 24 bits mais sur 8 bits.
—
En niveaux de gris (noir et blanc), chaque pixel est codé sur 8 bits, soit 1 octet.
—
La taille de l’image sera donc 3 fois plus petite qu’une image de même dimension en couleurs (mais elle sera en niveaux de gris…)
—
ATTENTION !! Les énoncés comportent parfois des pièges et une image en niveaux de gris peut très bien être codée sur 24 bits par pixel et non 8 (ce n’est pas très intelligent mais c’est comme ça…).
Il faut donc bien lire l’énoncé et s’adapter, il faut bien avoir cela en tête !
—
Tu trouveras sur cette page tous les exercices sur ce chapitre !
Retour au sommaireHaut de la page


