Sommaire
Introduction
Etude d’un cycle : calcul de Q et W
Principe de fonctionnement
Etude des moteurs : rendement de Carnot
Efficacité des PAC et des MF
Etude du cycle de Carnot
Etude du cycle de Beau de Rochas
Etude du cycle diesel
Complément : inexistence du moteur monotherme
Exercices
Dans ce chapitre nous allons étudier le principe de fonctionnement (d’un point de vue thermodynamique) des machines thermiques, comme les moteurs, les réfrigérateurs, les centrales nucléaires etc…
Il s’agit d’une application très courante du cours sur le premier et le second principe de la thermodynamique qu’il faut absolument maîtriser avant de lire ce qui suit !
Tu es donc fortement invité à aller voir ces chapitres si ce n’est pas encore fait 
Lien vers le chapitre sur le premier principe.
Lien vers le chapitre sur le second principe.
Nous étudierons d’abord le principe de fonctionnement général des différentes machines avant de voir des cycles particuliers.
Une petite démonstration complémentaire viendra clôturer le chapitre.
Toutes les machines étudiées fonctionneront selon un cycle, c’est-à-dire que l’état initial et l’état final seront les mêmes.
On peut en déduire que tout ce qui est noté avec Δ (ΔU, ΔS, ΔT etc…) sera nul !
Dans ce chapitre, on se servira principalement de ΔU et ΔS :
\(\displaystyle \Delta U_{cycle} = 0 \)
\(\displaystyle \Delta S_{cycle} = 0 \)
W et Q en revanche ne sont pas nuls (on rappelle que ce ne sont pas des fonctions d’état, donc ils ne s’écrivent pas avec Δ).
Dans le diagramme de Clapeyron (P ; V), un cycle pourra se représenter de la manière suivante (les flèches indiquent le sens de parcours du cycle) :
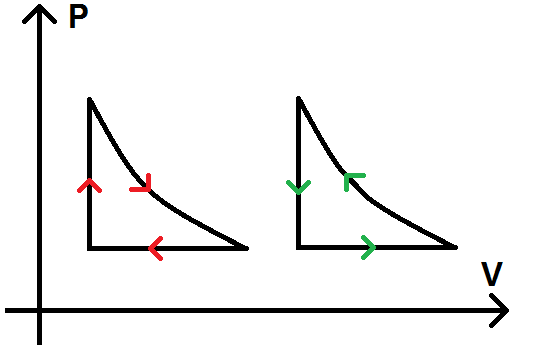
Le cycle pourra être parcouru dans le sens horaire (sens des aiguilles d’une montre, cycle de gauche sur le diagramme ci-dessus) ou dans le sens trigonométrique (sens inverse des aiguilles d’une montre, aussi appelé sens antihoraire, cycle de droite sur le diagramme ci-dessus). Cela aura toute son importance pour le signe de W !
En effet, le travail d’un cycle correspond à + ou – l’aire à l’intérieur du cycle dans le diagramme de Clapeyron :
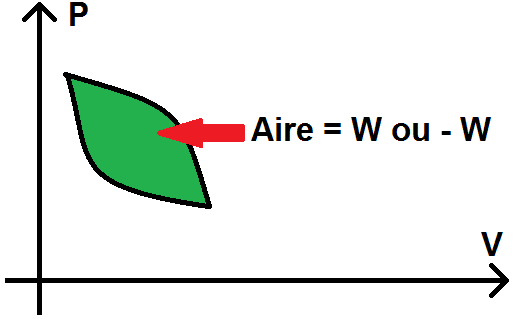
Voyons pourquoi sur un exemple simple, qui pourra se généraliser.
On va prendre un cycle à 4 étapes (notées 1, 2, 3 et 4) dont la représentation dans le diagramme (P ; V) est rectangulaire, c’est-à-dire composé de deux isobares et deux isochores. Pour notre exemple, ce cycle s’effectuera dans le sens horaire :
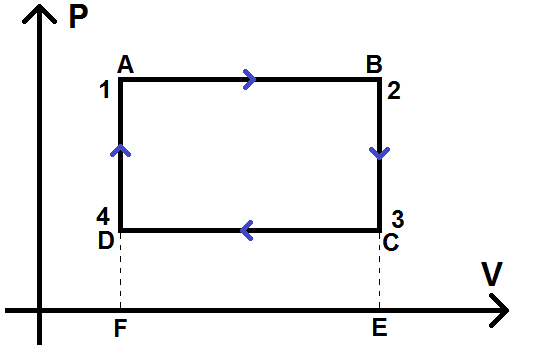
On hachure en vert le rectangle ABEF et en rouge DCEF pour la suite de la démonstration :
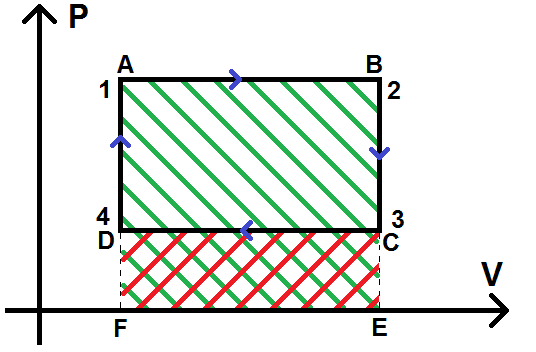
On avait vu dans le chapitre sur le 1er principe que le travail entre 2 étapes correspond à l’aire sous la courbe : elle est négative si on va de gauche à droite, et positive si on va de droite à gauche.
Le travail de 1 à 2, noté W1,2, correspond à l’opposé de l’aire hachurée en vert (opposé car on va de gauche à droite donc W1,2 < 0) : W1,2 = – AireABEF
W3,4 correspond à l’aire hachurée en rouge (W3,4 > 0 car on va de droite à gauche) :
W3,4 = AireDCEF
W2,3 = 0 et W4,1 = 0 car pas d’aire sous la courbe (transformations isochores).
W = W1,2 + W2,3 + W3,4 + W4,1
W = – AireABEF + AireDCEF = – Averte + Arouge
Autrement dit W = – Aireintérieur cycle
Le signe – vient du fait que l’aire verte est plus grande que l’aire rouge.
Ici W est négatif car on a parcouru le cycle dans le sens horaire, et on pourrait montrer facilement qu’il aurait été positif dans le cas contraire.
Cet exemple peut se généraliser et on peut en déduire la règle suivante :
—
Pour un cycle, W correspond à + ou – l’aire intérieur du cycle dans le diagramme de Clapeyron.
W < 0 si le cycle est parcouru dans le sens horaire ;
W > 0 si le cycle est parcouru dans le sens trigonométrique.
—
Si on a 2 cycles sur le même graphique, on pourra facilement comparer leur aire intérieure pour comparer W par exemple.
Attention, on parle bien ici du diagramme de Clapeyron (P ; V) : on a vu qu’il existe d’autres diagrammes comme (P ; T) ou (T ; S), mais l’aire à l’intérieur d’un cycle ne correspondra pas dans ces diagrammes au travail…
Avec W, on peut facilement trouver Q, car d’après le 1er principe, ΔUcycle = Wcycle + Qcycle.
Mais ΔUcycle = 0 car c’est un cycle, donc Wcycle + Qcycle = 0, donc Qcycle = – Wcycle.
Attention, on parle ici du Q et du W sur tout le cycle, mais chaque transformation (de 1 à 2, de 2 à 3 etc…) peut être étudiée séparément et avoir son propre ΔU, Q et W.
On aura ainsi ΔU1,2, Q1,2, W1,2, ΔU2,3, Q2,3, W2,3 etc… et on pourra appliquer le fait que Qcycle = Q1,2 + Q2,3 + … et idem pour W et ΔU.
C’est ce que nous ferons d’ailleurs quand nous étudierons plus loin dans le chapitre des cycles particuliers.
Voyons maintenant le principe de fonctionnement des machines.
Toutes les machines que l’on étudiera sont des machines dithermes, c’est-à-dire qu’elles utilisent deux sources de chaleur : une source froide et une source chaude, avec lesquelles les machines vont réaliser des échanges thermiques.
A noter qu’il existe des machines trithermes utilisant trois sources de chaleur, mais pas de moteur monotherme !
La démonstration de l’inexistence des moteurs monothermes sera faite en fin de chapitre.
L’échange de chaleur avec la source froide sera noté Qf et celui avec la source chaude sera noté Qc.
On distingue alors deux types de machines thermiques :
– les moteurs thermiques, qui convertissent l’énergie thermique en travail ;
– les machines de transfert de chaleur, qui servent à créer du chaud et que l’on appelle pompe à chaleur, ou du froid et que l’on appelle machine frigorifique.
Pompe à chaleur est parfois abrégée PAC et machine frigorifique MF.
Étudions la différence entre ces 2 types de machine.
Un moteur thermique prend de l’énergie à la source chaude (Qc) et la convertit en travail (W).
Toute l’énergie thermique ne peut cependant être convertie en travail et il y a donc des pertes, qui sont rejetées sous forme de chaleur à la source froide (Qf).
On a donc le schéma suivant :
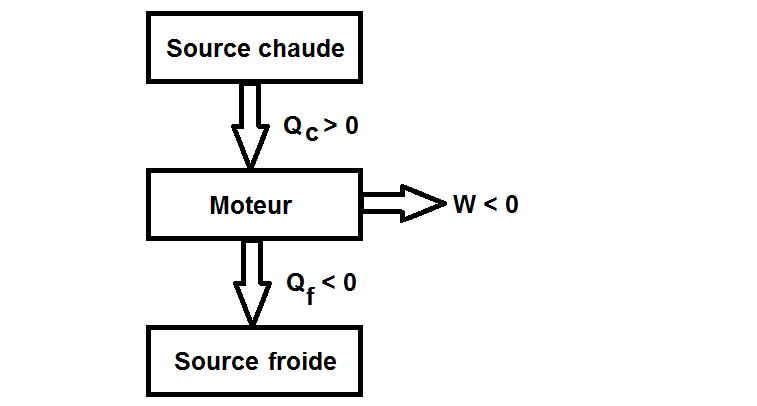
On a donc Qc > 0, Qf < 0 et W < 0 pour un moteur thermique
A l’inverse, une machine de transfert de chaleur prend de la chaleur à la source froide (Qf) et du travail (W) puis restitue toute cette énergie à la source chaude (Qc).
On a donc le schéma suivant, qui est tout l’inverse du précédent !
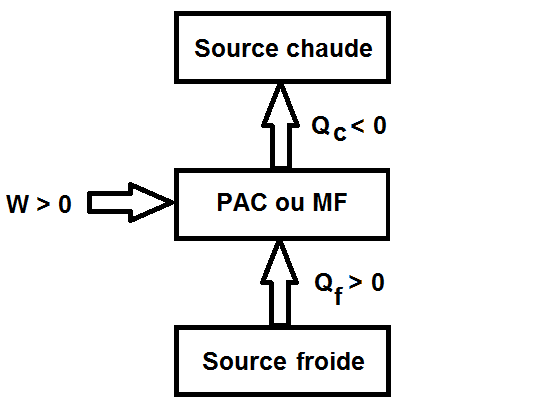
On a donc Qc < 0, Qf > 0 et W > 0 pour une pompe à chaleur ou une machine frigorifique, tout l’inverse du moteur !
—
ATTENTION !! Tu verras peut-être parfois que les Q et W sont tous positifs, et qu’il faut alors mettre un signe – quand l’énergie est cédée pour l’application des formules (1er et second principes notamment). Il est fortement déconseillé de suivre cette méthode car cela embrouille plus qu’autre chose !!
—
Remarque : W > 0 pour les PAC/MF et W < 0 pour les moteurs, donc dans le diagramme (P ; V), le cycle d’une PAC/MF se fera toujours dans le sens trigo, le cycle d’un moteur se fera toujours dans le sens horaire.
Mais dans le cas de machine de transfert de chaleur, comment distinguer les pompes à chaleur des machines frigorifiques ?
Le principe est très simple : tout dépend de la grandeur qui nous intéresse !
En effet, dans le cas d’une pompe à chaleur, ce qui intéresse l’utilisateur est de chauffer la source chaude, c’est donc Qc qui l’intéresse.
En revanche, pour une machine frigorifique, l’utilisateur souhaite refroidir la source froide, c’est donc Qf qui l’intéresse.
Et pour les deux types de machine, ce qui coûte c’est W (souvent du travail électrique).
On a donc deux expressions de rendement différentes :
\(\displaystyle \eta_{frigorifique} = \frac{Q_f}{W} \)
\(\displaystyle \eta_{PAC} = \frac{-Q_c}{W} \)
Le signe – vient du fait que Qc est négatif.
—
Pour les PAC et les machines frigorifiques, on parlera plutôt d’efficacité et non de rendement, nous verrons plus loin pourquoi.
—
Pour un moteur, ce qui intéresse l’utilisateur c’est le travail W en sortie, et ce qui coûte c’est la chaleur prise à la source chaude Qc (on a vu que la chaleur Qf correspond à des « déchets »), d’où
\(\displaystyle \eta_{moteur} = \frac{-W}{Q_c} \)
Là encore le signe – vient du fait que W est négatif pour un moteur.
Pour un moteur on parle bien de rendement en revanche.
Étudions maintenant plus en détail ce moteur.
Comme on vient de le voir :
\(\textstyle \eta_{moteur} = \frac{-W}{Q_c} \)
Comme on l’a vu précédemment, ΔU = 0 et ΔS = 0 car le moteur fonctionne selon un cycle.
Appliquons le premier et le second principe de la thermodynamique :
ΔU = Qc + Qf + W = 0
Donc -W = Qc + Qf
Remplaçons alors dans la formule :
\(\textstyle \eta_{moteur} = \frac{Q_c + Q_f}{Q_c} \)
\(\textstyle \eta_{moteur} = 1 + \frac{Q_f}{Q_c} \)
Comme Qc > 0 et Qf < 0, Qf/Qf < 0, d'où :
\(\textstyle \eta_{moteur} \lt 1 \)
On pouvait s’en douter, un moteur consomme de l’énergie donc son rendement est nécessairement inférieur à 1 (sinon ça se saurait !).
Appliquons maintenant le second principe :
ΔS = Séch + Scréée = 0
Les transferts thermiques avec les sources chaude et froide seront toujours considérés à température constante Tf et Tc, d’où :
\(\textstyle S_{ech} = \int_c \frac{dQ}{T} + \int_f \frac{dQ}{T} \)
\(\textstyle S_{ech} = \frac{1}{T_c} \int_c dQ + \frac{1}{T_f} \int_f dQ \)
\(\displaystyle S_{ech} = \frac{Q_c}{T_c} + \frac{Q_f}{T_f} \)
Cette formule sera vraie pour les moteurs, les PAC et les MF.
1er cas : cycle réversible
On a donc Scréée = 0, d’où Séch = 0 (cat ΔS = 0).
D’où :
\(\textstyle \frac{Q_c}{T_c} + \frac{Q_f}{T_f} = 0 \)
\(\textstyle \frac{Q_f}{T_f} = -\frac{Q_c}{T_c} \)
\(\textstyle \frac{Q_f}{Q_c} = -\frac{T_f}{T_c} \)
D’où :
\(\displaystyle \eta_{moteur \, rev} = 1 – \frac{T_f}{T_c} \)
rendement d’un moteur à cycle réversible
Ce rendement est appelé rendement de Carnot : nous allons voir qu’il s’agit du rendement maximal d’un moteur.
2ème cas : cycle irréversible
On a donc Scréée > 0, d’où Séch < 0.
D'où :
\(\textstyle \frac{Q_c}{T_c} + \frac{Q_f}{T_f} \lt 0 \)
\(\textstyle \frac{Q_f}{T_f} \lt -\frac{Q_c}{T_c} \)
\(\textstyle \frac{Q_f}{Q_c} \lt -\frac{T_f}{T_c} \)
On en déduit que
\(\displaystyle \eta_{moteur, \, irrev} \lt 1 – \frac{T_f}{T_c} \)
\(\displaystyle \eta_{moteur \, irrev} \lt \eta_{moteur \, rev} \)
Cela démontre qu’un moteur dont le cycle est irréversible à un rendement inférieur à celui dont le cycle est réversible : le rendement de Carnot correspond donc au rendement maximum d’un moteur.
Nous allons maintenant faire la même chose pour les PAC et le MF.
Reprenons la même étude dans le cas des PAC et des MF, mais uniquement dans le cas réversible, car il n’y a que dans ce cas que l’on va obtenir des formules intéressantes.
Puisque l’on se place dans le cas réversible, d’après le même calcul que précédemment, on a :
\(\textstyle \frac{Q_f}{Q_c} = -\frac{T_f}{T_c} \)
Donc :
\(\textstyle \frac{Q_c}{Q_f} = -\frac{T_c}{T_f} \)
De plus, d’après le 1er principe, ΔU = Qc + Qf + W = 0
Donc W = -Qc – Qf
Commençons les PAC, on a vu que :
\(\textstyle \eta = \frac{-Q_c}{W} \)
\(\textstyle \eta = \frac{-Q_c}{-Q_c – Q_f} \)
En divisant par -Qc, on obtient :
\(\textstyle \eta = \frac{1}{1 + \frac{Q_f}{Q_c}} \)
\(\textstyle \eta = \frac{1}{1 – \frac{T_f}{T_c}} \)
On multiplie par Tc :
\(\displaystyle \eta_{PAC} = \frac{T_c}{T_c – T_f} \)
pour un cycle réversible
Or Tc > Tc – Tf, on en déduit que :
\(\displaystyle \eta_{PAC} \gt 1 \)
On trouve donc une efficacité plus grande que 1 !!! 


C’est la raison pour laquelle on parle d’efficacité et non de rendement comme dans le cas d’un moteur.
Cela ne signifie pas pour autant que la PAC crée de l’énergie. Cela est dû au fait que la PAC, tout comme la MF, prend de l’énergie à la source froide pour la donner à la source chaude, ce qui se fait normalement naturellement !
Tout comme pour le moteur, l’efficacité trouvée dans le cas réversible correspond à l’efficacité maximum : pour un cycle irréversible, l’efficacité est moindre, d’où :
\(\displaystyle \eta_{PAC \, max} = \frac{T_c}{T_c – T_f} \)
Passons maintenant à l’étude d’une machine frigorifique, qui sera fortement similaire.
On a vu que :
\(\textstyle \eta = \frac{Q_f}{W} \)
\(\textstyle \eta = \frac{Q_f}{-Q_f – Q_c} \)
En divisant par -Qf, on obtient :
\(\textstyle \eta = \frac{-1}{1 + \frac{Q_c}{Q_f}} \)
\(\textstyle \eta = \frac{-1}{1 – \frac{T_c}{T_f}} \)
On multiplie par Tf :
\(\textstyle \eta = \frac{-T_f}{T_f – T_c} \)
Tf – Tc étant négatif, on passe le signe – au dénominateur, ce qui donne :
\(\displaystyle \eta_{MF} = \frac{T_f}{T_c – T_f} \)
pour un cycle réversible
On retrouve presque la même expression que pour la PAC, avec Tf à la place de Tc au numérateur.
Contrairement à la PAC, l’efficacité peut être plus petite que 1 mais les valeurs de Tc et Tf sont telles que ce n’est presque jamais le cas.
Evidemment, là encore il s’agit du rendement maximal :
\(\displaystyle \eta_{MF \, max} = \frac{T_f}{T_c – T_f} \)
Maintenant que l’on a vu le principe général de fonctionnement de toutes ces machines, nous allons pouvoir étudier en détail quelques cycles particuliers que l’on retrouve souvent en exercice.
Le cycle de Carnot est un des plus répandus dans les exercices que tu rencontreras.
Il se décompose de la façon suivante :
1 à 2 : détente isotherme à la température Tc (avec apport de chaleur Qc)
2 à 3 : détente adiabatique réversible pour amener à la température Tf
3 à 4 : compression isotherme à la température Tf (avec refroidissement Qf)
4 à 1 : compression adiabatique réversible pour revenir à la température Tc
Le but est de trouver l’expression du rendement de ce moteur en fonction de Tf et Tc.
Remarque : le cycle n’étant a priori pas réversible, on ne peut pas utiliser directement la formule du rendement de Carnot… mais puisque ce cycle s’appelle cycle de Carnot, il y a fort à parier que l’on retrouve l’expression du rendement de Carnot 
Comme on a une détente isotherme à la température Tc de 1 à 2, on en déduit que :
T1 = T2 = Tc
Comme on a une compression isotherme à la température Tf de 3 à 4, on en déduit que :
T3 = T4 = Tf
Dans le diagramme (P ; V), on obtient :
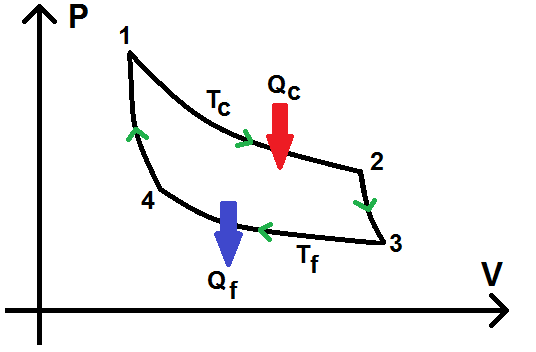
Étudions séparément chacune des transformations :
de 1 à 2 : isotherme donc ΔU1,2 = 0 donc Q1,2 = -W1,2.
D’après l’énoncé Q1,2 = Qc, et on sait que pour une isotherme :
\(\textstyle W_{1,2} = nRT_c ln(\frac{V_1}{V_2}) \)
D’où :
\(\textstyle Q_c = -nRT_c ln(\frac{V_1}{V_2}) \)
\(\textstyle Q_c = nRT_c ln(\frac{V_2}{V_1}) \)
De la même manière, pour la compression isotherme de 3 à 4, on montrerait que :
\(\textstyle Q_f = nRT_f ln(\frac{V_4}{V_3}) \)
Pour la détente de 2 à 3, celle-ci étant adiabatique, on va pouvoir utiliser les formules de Laplace.
Oui mais laquelle ??
Les calculs ci-dessus ont fait apparaître les volumes, et on souhaite faire apparaître les températures (car on veut le rendement en fonction de Tf et Tc), on va donc utiliser la formule de Laplace entre V et T :
\(\textstyle TV^{\gamma – 1} = constante \)
D’où pour la transformation de 2 à 3 :
\(\textstyle T_3V_3 ^{\gamma – 1} = T_2V_2 ^{\gamma – 1} \)
De la même manière, pour l’adiabatique de 4 à 1 :
\(\textstyle T_4V_4 ^{\gamma – 1} = T_1V_1 ^{\gamma – 1} \)
Divisons la deuxième équation par la première, cela donne :
\(\textstyle \frac{T_4V_4 ^{\gamma – 1}}{T_3V_3 ^{\gamma – 1}} = \frac{T_1V_1 ^{\gamma – 1}}{T_2V_2 ^{\gamma – 1}} \)
Or on a vu que T1 = T2 et T3 = T4, donc :
\(\textstyle (\frac{V_4}{V_3})^{\gamma – 1} = (\frac{V_1}{V_2})^{\gamma – 1} \)
\(\textstyle \frac{V_4}{V_3} = \frac{V_1}{V_2} \)
En reprenant l’expression de Qf et Qc trouvées précédemment avec les volumes, on a :
\(\textstyle \frac{Q_f}{Q_c} = -\frac{nRT_fln(\frac{V_4}{V_3})}{nRT_cln(\frac{V_2}{V_1})} \)
\(\textstyle \frac{Q_f}{Q_c} = -\frac{T_fln(\frac{V_4}{V_3})}{T_cln(\frac{V_4}{V_3})} \)
\(\textstyle \frac{Q_f}{Q_c} = -\frac{T_f}{T_c} \)
Or le rendement d’un moteur est :
\(\textstyle \eta _{moteur} = 1 + \frac{Q_f}{Q_c} \)
\(\textstyle \eta _{moteur} = 1 – \frac{T_f}{T_c} \)
On retrouve la formule du rendement de Carnot !!
Ainsi le rendement d’un cycle de Carnot est… le rendement de Carnot. 
Un cycle de Carnot est donc réversible.
L’étude ci-dessus est typique du genre d’étude que tu auras à faire dans les exercices sur les cycles moteurs : il s’agit d’étudier chaque transformation séparément puis de les regrouper en utilisant le 1er et le second principe.
Voyons un deuxième exemple de cycle très courant : le cycle Beau de Rochas.
Le cycle Beau de Rochas est également un cycle à 4 temps, qui se décompose de la manière suivante :
1 à 2 : compression adiabatique du mélange (air-carburant) jusqu’à Vmin.
2 à 3 : combustion (apport de chaleur Qc) isochore.
3 à 4 : détente adiabatique jusqu’à Vmax
4 à 1 : refroidissement isochore (perte de chaleur Qf)
Dans le diagramme (P ; V), on a :
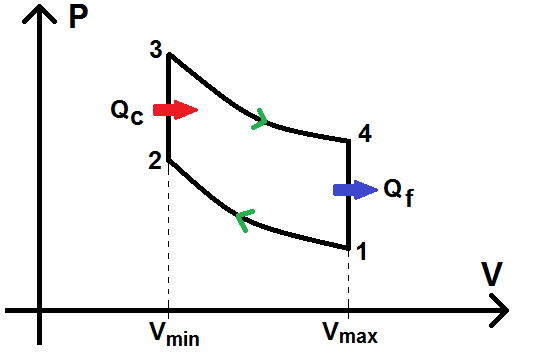
On a donc :
V1 = V4 = Vmax, et V2 = V3 = Vmin
On souhaite exprimer le rendement en fonction d’une constante α appelée taux de compression volumétrique définie par :
\(\textstyle \alpha = \frac{V_{max}}{V_{min}} \)
Étudions comme précédemment les transformations séparément.
Commençons par les 2 isochores.
Pour la combustion de 2 à 3, comme elle est isochore :
\(\textstyle Q_{2,3} = C_v \Delta T \)
D’après l’énoncé Q2,3 = Qc, donc :
\(\textstyle Q_c = C_v (T_3 – T_2) \)
De la même manière, pour le refroidissement isochore de 4 à 1 :
\(\textstyle Q_f = C_v (T_1 – T_4) \)
Passons maintenant aux adiabatiques : on peut utiliser les formules de Laplace.
Oui mais laquelle ?
Les calculs ci-dessus ont fait apparaître les températures, et on souhaite faire apparaître les volumes (car on veut le rendement en fonction de α = Vmax/Vmin), on va donc utiliser la formule de Laplace entre V et T :
\(\textstyle TV^{\gamma – 1} = constante \)
D’où pour la transformation de 1 à 2 :
\(\textstyle T_1V_1 ^{\gamma – 1} = T_2V_2 ^{\gamma – 1} \)
De la même manière, pour l’adiabatique de 4 à 1 :
\(\textstyle T_4V_4 ^{\gamma – 1} = T_3V_3 ^{\gamma – 1} \)
N’oublions pas que : V1 = V4 = Vmax, et V2 = V3 = Vmin
D’où :
\(\textstyle T_1V_{max} ^{\gamma – 1} = T_2V_{min} ^{\gamma – 1} \)
De la même manière, pour l’adiabatique de 4 à 1 :
\(\textstyle T_4V_{max} ^{\gamma – 1} = T_3V_{min} ^{\gamma – 1} \)
En soustrayant terme à terme ces deux équations et en factorisant par le volume, on obtient :
\(\textstyle (T_4 – T_1)V_{max} ^{\gamma – 1} = (T_3 – T_2)V_{min} ^{\gamma – 1} \)
D’où :
\(\textstyle \frac{T_4 – T_1}{T_3 – T_2} = (\frac{V_{min}}{V_{max}})^{\gamma – 1} \)
\(\textstyle \frac{T_4 – T_1}{T_3 – T_2} = (\frac{V_{max}}{V_{min}})^{1 – \gamma} \)
\(\textstyle \frac{T_4 – T_1}{T_3 – T_2} = \alpha^{1 – \gamma} \)
Reprenons maintenant les expressions de Qfet Qc trouvées précédemment :
\(\textstyle \frac{Q_f}{Q_c} = \frac{C_v(T_1 – T_4)}{C_v(T_3 – T_2)} \)
\(\textstyle \frac{Q_f}{Q_c} = -\frac{T_4 – T_1}{T_3 – T_2} \)
\(\textstyle \frac{Q_f}{Q_c} = – \alpha^{1 – \gamma} \)
Or le rendement d’un moteur est :
\(\textstyle \eta _{moteur} = 1 + \frac{Q_f}{Q_c} \)
\(\textstyle \eta _{moteur} = 1 – \alpha^{1 – \gamma} \)
On vient de trouver le rendement en fonction de α 
Remarque : le cycle Beau de Rochas est parfois modélisé avec un état supplémentaire (que l’on appellera 0) et 2 transformations supplémentaires :
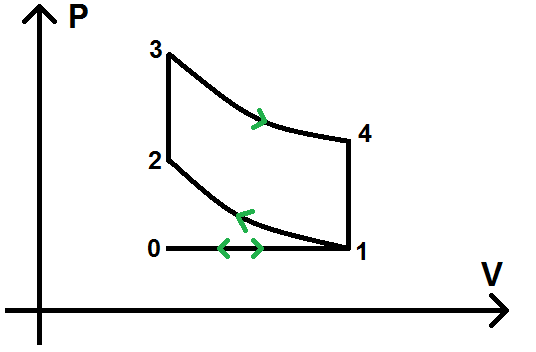
Le cycle n’est donc plus 1-2-3-4 comme précédemment mais 0-1-2-3-4.
Il y a donc 2 étapes supplémentaires : de 0 à 1 et de 1 à 0.
L’étape 0-1 correspond à l’admission du mélange air-carburant
L’étape 1-0 correspond à l’échappement des gaz brûlés par le moteur
Puisque la transformation 0-1 est la transformation inverse de 1-0, les 2 étapes vont « s’annuler » dans le cycle et cela ne change donc strictement rien à l’étude réalisée précédemment !!!
C’est pourquoi souvent en exercice cette étape est absente et on a uniquement le cycle 1-2-3-4 comme étudié précédemment.
Dernier cycle que nous étudierons car il se rencontre souvent : le cycle diesel.
Le cycle diesel est très similaire au cycle Beau de Rochas, à une exception près : la combustion isochore 2-3 est remplacée par une combustion isobare :
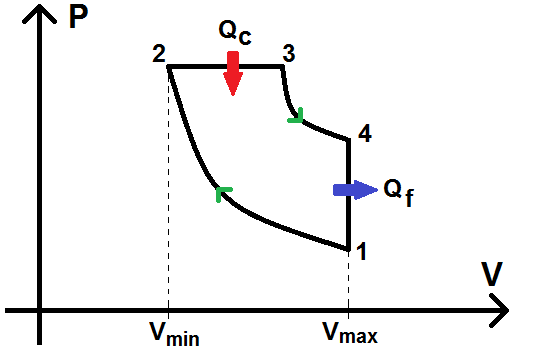
La seule chose qui va changer par rapport au cycle Beau de Rochas est donc l’expression de Qc correspondant à la transformation 2-3. Celle-ci étant isobare et non isochore comme précédemment, on a donc :
\(\textstyle Q_c = C_p (T_3 – T_2) \)
Remarque : on a juste remplacé le Cv par Cp.
On reprend l’expression de Qf trouvée dans l’étude du cycle Beau de Rochas :
\(\textstyle \frac{Q_f}{Q_c} = \frac{C_v(T_1 – T_4)}{C_p(T_3 – T_2)} \)
\(\textstyle \frac{Q_f}{Q_c} = – \frac{C_v}{C_p }\frac{T_4 – T_1}{T_3 – T_2} \)
On rappelle que Cv/Cp = 1/γ :
\(\textstyle \frac{Q_f}{Q_c} = – \frac{1}{\gamma} \alpha^{1 – \gamma} \)
Or le rendement d’un moteur est :
\(\textstyle \eta _{moteur} = 1 + \frac{Q_f}{Q_c} \)
\(\textstyle \eta _{moteur} = 1 – \frac{1}{\gamma} \alpha^{1 – \gamma} \)
On retrouve exactement la même formule que pour le cycle Beau de Rochas mais avec 1/γ en plus.
γ étant plus grand que 1, on montre facilement que le rendement du moteur diesel est plus élevé que celui du cycle Beau de Rochas (si α est le même évidemment).
Nous allons démontrer l’inexistence d’un moteur monotherme.
Cette démonstration est mise à la fin du chapitre car elle n’est pas indispensable au reste du cours, c’est juste une démonstration qui peut faire partie d’un exercice, ou t’être demandée en colle par exemple.
Nous allons raisonner par l’absurde : supposons donc qu’un tel moteur monotherme existe. Un moteur fournit du travail, donc W < 0.
D’après le 1er principe, ΔU = W + Q = 0 car c’est un cycle, donc Q = -W.
On en déduit que Q > 0 : le moteur prélève de la chaleur à une source :

Or d’après le second principe, ΔS = Séch + Scréée = 0 car c’est un cycle.
Comme Scréée ≥ 0, on a Séch ≤ 0.
Or :
\(\textstyle S_{ech} = \frac{Q}{T} \)
T ≥ 0 donc Q ≤ 0 : contradiction car on a dit précédemment Q > 0 !!
Donc un moteur monotherme n’existe pas.
Cette inexistence est liée à l’incompatibilité entre le premier et le second principe si on suppose W < 0 au début comme on l'a fait (car on a considéré un moteur).
En revanche, si on suppose au début W > 0, il n’y a plus d’incompatibilité car on aurait Q < 0 d'après le 1er principe, ce qui est compatible avec le second principe.
C’est ce que l’on appelle l’énoncé de Kelvin, selon lequel une machine monotherme ne peut transformer toute la chaleur reçue en travail, mais elle peut transformer du travail reçu en chaleur.
—
Énoncé de Kelvin : un système en contact avec une seule source de chaleur ne peut, au cours d’un cycle, que recevoir du travail et fournir de la chaleur, mais pas l’inverse.
—
Cet énoncé peut différer d’un professeur à l’autre, c’est l’idée qu’il est important de retenir.
Le cours sur les machines thermiques est désormais terminé, il ne reste plus qu’à t’entraîner à faire des exercices ! 
Les exercices sur ce chapitre seront bientôt disponibles !
Sommaire des coursHaut de la page


