Tu trouveras ici tous les exercices sur les équations horaires.
N’hésite pas à aller d’abord voir le cours sur les équations horaires avant de faire les exercices 
Sommaire
Exercice classique
Mouvement d’une particule dans un champ électrique
Service au tennis
Les premières vidéos vont consister à redémontrer les expressions classiques trouvées dans le cours dans le cas du schéma suivant :
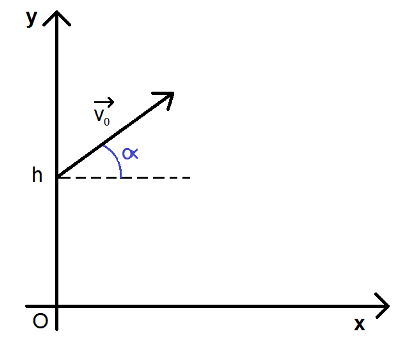
On a une balle de masse m initialement à l’altitude h, lancée avec une vitesse initiale de norme v0, le vecteur vitesse faisant un angle α avec l’axe horizontal.
1) Trouver les coordonnées du vecteur accélération.
2) Trouver les coordonnées du vecteur vitesse.
3) Trouver les équations horaires donnant la position de la balle au cours du temps.
4) Trouver l’équation de la trajectoire.
5) Trouver les coordonnées du sommet.
6) Trouver les coordonnées du point de chute de la balle dans le cas où h = 0.
On considère un électron qui entre dans une zone où règne un champs électrique créé par deux plaques de longueur L, l’une chargée positivement, l’autre négativement selon le schéma ci-dessous.
Initialement, l’électron est en O et entre dans la zone avec une vitesse horizontale V0 selon l’axe x.
Données : masse d’un électron : me- = 9,1 x 10 -31 kg
charge élémentaire : e = 1,6 x 10 -19 C
champs électrique : E = 10 V
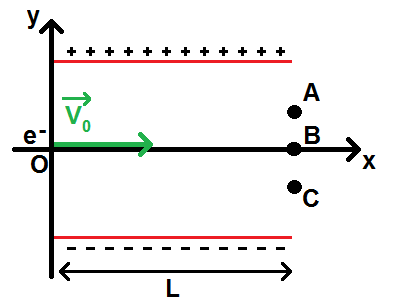
1) On note P le poids de l’électron. Montrer que P << Fe
2) L’électron va-t-il arriver en A, en B ou en C ?
3) Calculer l’ordonnée du point de sortie.
Cet exercice est tiré du bac Amérique du Sud 2009.
Un joueur de tennis effectue un service depuis un point O. La balle est à la verticale du point O, à une hauteur H = 2,20 m du sol.
La balle, de masse m = 58,0 g, est frappée avec une vitesse horizontale v0 = 126 km/h.
Le point O est situé à 12,2 m du filet, qui mesure 0,920 m de haut.
Le joueur cherche à faire atterrir la balle au point B tel que OB = L = 18,7 m. Si la balle tombe plus loin, le service est faux.
La situation est résumée dans le schéma ci-dessous :
1) Montrer que le problème est plan.
2) Montrer que le service est faux. En réalité il est juste : pourquoi ?



Merci beaucoup j’ai trouvé ce que je cherchais 🙏🙏
J’aime vos démonstrations. Merci
Au niveau de l’exercice dont on a demandé là où arrivera l’électron, j’aimerais savoir s’il est possible de déterminer d’abord l’équation de la trajectoire et enfin affirmer que, puis que la trajectoire est parabolique et positive alors l’électron arrivera à point À.
Oui tout à fait.
Bonjour,
Pour déterminer la distance à laquelle le projectile touchera le sol.Au lieu de factoriser le polynôme de second degré, ne pourrait-on pas tout simplement utiliser le fait que la racine 2(qui représente la distance) correspond à la symétrique, par rapport à l’abcisse du sommet, de la racine1. Or puisque la racine 1=0 donc racine2=2*abscisse du sommet= distance. Ou bien faut-il obligatoirement passer par une factorisation.
En effet mais là c’est un peu plus mathématique, et le fait que la racine 2 est la symétrique par rapport au sommet de la première racine n’est pas une propriété que l’on utilise généralement (même si cela est vrai).
L’intérêt de la factorisation est de trouver l’expression littérale de la deuxième racine !