Sommaire
Introduction
Chute verticale
Mouvement parabolique
Exercices
Ce chapitre est la suite du préambule sur les équations horaires que tu dois bien maîtriser avant de lire ce qui suit. Nous étudierons d’abord un cas simple avant de passer à un cas un peu plus compliqué.
Si tu sens prêt, c’est parti !
Remarque : tout comme dans le chapitre précédent, certains vecteur seront notés en gras, sans la flèche au-dessus.
Passons maintenant aux choses sérieuses ! Nous allons commencer par étudier un cas simple, le cas d’une chute verticale.
C’est plus simple car il n’y a qu’une seule dimension (un seul axe). Après en 2D ce sera le même principe avec quelques particularités en plus^^
On a une balle de masse m = 15 g qui tombe dans le vide, lâchée sans vitesse initiale à 20 m au-dessus du sol. On note h cette hauteur.
On néglige les frottements de l’air, et on demande de trouver l’équation de la trajectoire. On donne g = 10 m.s-2
L’axe vertical (Oz) est dirigé vers le haut. On peut donc faire le schéma suivant :
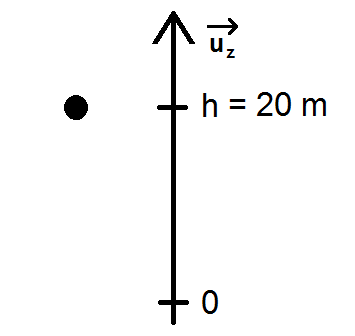
On commence toujours par appliquer la deuxième loi de Newton comme expliqué dans le chapitre précédent :
\(\textstyle \sum \vec{F} = m \vec{a} \)
Comme on néglige les frottements la balle n’est soumise qu’au poids :
\(\displaystyle \vec{P} = m \vec{a} \)
\(\displaystyle -m g\vec{u_z} = m \vec{a} \)
\(\displaystyle -g\vec{u_z} = \vec{a} \)
On projette maintenant sur l’axe (Oz), cela donne :
\(\textstyle a = – g \)
Maintenant pour trouver la vitesse, on a dit qu’il fallait intégrer l’accélération. Mais on a dit qu’il fallait faire attention à rajouter une constante quand on fait la primitive en physique !!
La primitive de -g est donc -gt + K, avec K constante :
\(\textstyle v = -gt + K \)
Oui mais comment trouver K ?? Avec ce qu’on appelle les conditions initiales. Les conditions initiales sont les valeurs des différentes grandeurs à l’instant initial, c’es-à-dire à t = 0s.
Ici on dit que la balle est lâchée sans vitesse initiale, donc v(0) = 0 m.s-1
On remplace donc t par 0 dans la formule précédente (on rappelle que v est en fait v(t) ) :
\(\displaystyle v(0) = -g \times 0 + K \)
\(\displaystyle v(0) = K \)
Or v(0) = 0, donc K = 0 !
On remplace alors K par 0 dans l’équation, ce qui donne :
\(\textstyle v = -gt \)
On vient de trouver v !
—
Il faut que tu retiennes bien les étapes que l’on vient de voir ce sera tout le temps la même chose ! A savoir :
1) on intègre SANS OUBLIER LA CONSTANTE !!
2) On remplace t par 0 pour trouver la constante.
3) On remplace la constante par sa valeur dans l’équation trouvée.
—
On va d’ailleurs utiliser cette méthode pour trouver la position !
En effet, on a vu que pour trouver la position on devait intégrer la vitesse. De plus la primitive de t est t2/2, donc en intégrant la formule précédent cela nous donne :
\(\textstyle z = -g\frac{t^2}{2} + C \)
—
ATTENTION !! Ici la primitive de v est z car c’est l’axe (Oz). Evidemment si c’était l’axe (Ox) on aurait mis x et non z, de même avec (Oy). Tout dépend de l’énoncé.
Dans les trajectoires paraboliques on aura vx, vy et vz, donc ce sera plus simple car vx donnera x, vy donnera y et vz donnera z.
—
—
ATTENTION !! Pense à mettre une constante différente d’avant pour ne pas t’embrouiller. Ici on a mis C mais on aurait pu prendre K’ par exemple ou toute autre lettre, du moment que ce n’est pas une lettre de l’énoncé (on ne prend pas g ou v par exemple…)
—
Comme tout à l’heure, et selon la méthode décrite plus haut, on doit trouver la constante entre remplaçant t par 0 :
\(\displaystyle z(0) = -g\frac{0^2}{2} + C \)
\(\displaystyle z(0) = C \)
Or z(0) = h car on rappelle qu’on a lâché la balle d’une hauteur initiale h.
Donc C = h.
Dernière étape : on remplace C par h dans l’équation, ce qui donne :
\(\textstyle z = -g\frac{t^2}{2} + h \)
Et là on a fini la deuxième partie puisque l’on a trouvé z.
—
ATTENTION ! L’énoncé dit que la hauteur initiale est de 20 m et que cette hauteur est notée h.
Et tu as remarqué qu’on a dit z(0)= h, et non z(0) = 20.
On aurait pu dire z(0) = 20 ce n’est pas faux mais on cherche toujours à avoir l’expression littérale (avec des lettres). De même on n’a pas remplacé g par 10 alors que cela est marqué dans l’énoncé.
Donc retiens que si il y a une grandeur qui est désignée par une lettre et dont tu connais la valeur, mets toujours la lettre d’abord. Tu pourras remplacer par la valeur quand on te demandera de calculer quelque chose (comme on va le faire en-dessous).
—
L’expression z = … est ce que l’on appelle l’équation horaire, car on rappelle que z est en fait z(t) : la position en fonction du temps (d’où le terme « horaire »).
A partir de cette équation on peut te demander certaines choses.
Par exemple on peut te demander au bout de combien de temps la balle va toucher le sol.
Pour ce faire, il faut traduire l’énoncé sous forme mathématique (comme souvent en physique).
Quand la balle va toucher le sol, on aura z = 0. On cherche donc t à partir de l’équation z = 0 :
\(\displaystyle z = 0 \)
\(\displaystyle -g\frac{t^2}{2} + h = 0 \)
\(\displaystyle -g\frac{t^2}{2} = -h \)
\(\displaystyle t^2 = \frac{2h}{g} \)
\(\displaystyle t = \sqrt{\frac{2h}{g}} \)
Et SEULEMENT MAINTENANT on peut remplacer par les chiffres car on a isolé ce que l’on voulait calculer :
\(\displaystyle t = \sqrt{\frac{2 \times 20}{10}} \)
\(\displaystyle t = \sqrt{4} \)
\(\displaystyle t = 2s \)
Donc au bout de 2s la balle va toucher le sol.
On peut te demander également à quelle vitesse la balle va toucher le sol.
Pour ce faire, rien de plus simple ! Maintenant que l’on sait qu’à t=2s, la balle touche le sol, il suffit de remplacer t par 2 dans l’expression de v (puisque l’on veut la vitesse) :
v = -gt
v = – 10 × 2
v = -20m.s-1
Mais, la vitesse est négative ?? En fait, c’est parce que l’axe vertical étant vers le haut, le vecteur vitesse est vers le bas dans la valeur est négative.
On vient en tout cas de trouver la vitesse au moment où la balle touchera le sol.
Remarque : tu t’es peut-être rendu compte que la masse de la balle n’intervenait absolument pas dans l’exercice. En effet, la masse s’annule dès les premières lignes quand on applique la 2ème loi de Newton. Donc même si elle apparaît dans l’énoncé elle n’apparaît pas dans les expressions recherchées.
—
Remarque : dès les 1ères lignes de calcul, on a eu a = -g (on aurait eu a = g si l’axe était vers le bas).
Donc g est égal à l’accélération dans le cas où l’objet n’est soumis qu’au poids (la pesanteur) : ceci explique le fait que g s’appelle l’accélération de la pesanteur !!
—
Une fois que tu as bien compris cet exemple (n’hésite pas à le refaire en voyant bien les différentes étapes de la méthode, et à faire des exercices similaires), on va pouvoir passer au niveau supérieur avec des trajectoires paraboliques 
Maintenant nous n’avons plus une, mais DEUX dimensions.
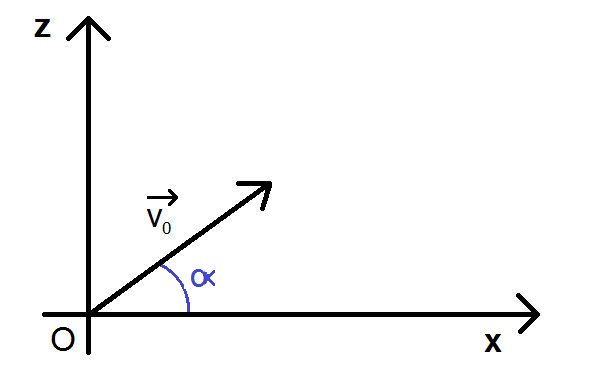
En fait nous avons une balle qui est lancée vers le haut ET vers l’avant depuis une hauteur h. Le vecteur vitesse initiale v0 fait un angle α avec l’horizontale. On néglige les frottements de l’air.
La plupart du temps on te donne le schéma qui suit donc tu n’auras pas à le faire (petit veinard  )
)
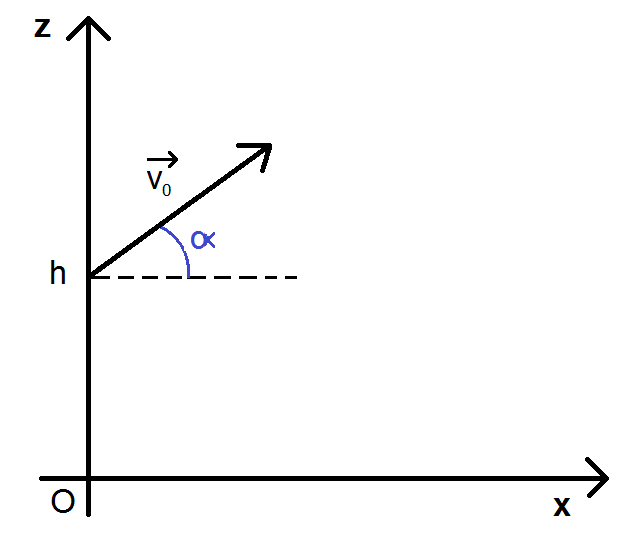
Si on reprend la méthode comme tout à l’heure, on commence par appliquer la deuxième loi de Newton :
\(\textstyle \sum \vec{F} = m \vec{a} \)
Comme on néglige les frottements la balle n’est soumise qu’au poids :
\(\displaystyle \vec{P} = m \vec{a} \)
\(\displaystyle -m g\vec{u_z} = m \vec{a} \)
\(\displaystyle -g\vec{u_z} = \vec{a} \)
Pour l’instant c’est exactement pareil que tout à l’heure… mais là ça va changer.
En effet, comme on est en 2D il faut projeter sur les deux axes : x et z.
Donc quand on projette le vecteur a, on a ax et az.
D’après ce qui précède le vecteur a est selon uz, donc ax = 0 et az = -g :
\(\textstyle \left\{ \begin{array}{c} a_x = 0 \\ a_z = -g \end{array} \right. \)
Si tu as bien suivi le chapitre précédent cela ne devrait pas te poser de problèmes 
Maintenant, comme on l’avait fait plus haut on va appliquer la méthode : 1) intégrer – 2) trouver la constante – 3) remplacer la constante dans l’équation
C’est parti ! On intègre (sans oublier la constante) :
\(\textstyle \left\{ \begin{array}{c} v_x = K \\ v_z = -gt + K \end{array} \right. \)
En effet, la primitive de 0 est une constante (K), la primitive de -g est -gt + constante.
—
Ici comme on a 2 constantes il faut forcément 2 lettres différentes, ou bien comme ici une lettre et la même avec « prime » : K et K’
—
On trouve les constantes en remplaçant t par 0 dans les deux équations :
\(\textstyle \left\{ \begin{array}{c} v_x(0) = K \\ v_z(0) = -g \times 0 + K’ \end{array} \right. \)
\(\textstyle \left\{ \begin{array}{c} v_x(0) = K \\ v_z(0) = K’ \end{array} \right. \)
Or vx(0) = v0 x cos(α), et vz(0) = v0 x sin(α) d’après le schéma (si tu as bien suivi le chapitre précédent une fois de plus).
D’où K = v0 x cos(α), et K’ = v0 x sin(α)
On remplace dans les équations :
\(\textstyle \left\{ \begin{array}{c} v_x = v_0 \times cos(\alpha) \\ v_z = -gt + v_0\times sin(\alpha) \end{array} \right. \)
Maintenant qu’on a trouvé la vitesse on va intégrer pour trouver la position (comme dans l’exemple de la chute verticale !).
On reprécise qu’ici la primitive de vx donne x et la primitive de vz donne z :
\(\textstyle \left\{ \begin{array}{c} x = v_0 \times cos(\alpha) \times t + C \\ z = -g\frac{t^2}{2} + v_0\times sin(\alpha) \times t + C’ \end{array} \right. \)
Comme tu vois les expressions (surtout celle de z) sont un peu plus longues que dans l’exercice de la chute verticale. Mais ça ne change rien à la méthode, on remplace t par 0 par trouver les constantes :
\(\textstyle \left\{ \begin{array}{c} x(0) = v_0 \times cos(\alpha) \times 0 + C \\ z(0) = -g\frac{0^2}{2} + v_0\times sin(\alpha) \times 0 + C \end{array} \right. \)
\(\textstyle \left\{ \begin{array}{c} x(0) = C \\ z(0) = C’ \end{array} \right. \)
Or x(0) = 0 et z(0) = h d’après le schéma, car x(0) et z(0) correspondent aux coordonnées du point à t = 0.
Donc C = 0 et C’ = h. Il n’y a plus qu’à remplacer :
\(\textstyle \left\{ \begin{array}{c} x = v_0 \times cos(\alpha) \times t \\ z = -g\frac{t^2}{2} + v_0\times sin(\alpha) \times t + h \end{array} \right. \)
Et là, OUFFFFFF !  tu as enfin trouvé les équations horaires !
tu as enfin trouvé les équations horaires !
On a donc les valeurs de x et z en fonction de t. Mais on va souvent te demander l’équation de la trajectoire, c’est-à-dire z en fonction de x, un peu comme une fonction en mathématiques. Cela va nous permettre de tracer le trajectoire du projectile.
Pour ce faire, on isole t dans l’expression la plus simple (ici celle de x), et on remplace dans l’autre :
\(\textstyle \left\{ \begin{array}{c} t = \frac{x}{v_0 \times cos(\alpha)} \\ z = -g\frac{(\frac{x}{v_0 \times cos(\alpha)})^2}{2} + v_0\times sin(\alpha) \times \frac{x}{v_0 \times cos(\alpha)} + h \end{array} \right. \)
\(\textstyle \left\{ \begin{array}{c} t = \frac{x}{v_0 \times cos(\alpha)} \\ z = -g\frac{x^2}{2 v_0^2cos^2(\alpha)} + x \times tan(\alpha) + h \end{array} \right. \)
L’équation de la trajectoire est donc :
\(\textstyle z(x) = -g\frac{x^2}{2 v_0^2 cos^2(\alpha)} + x \times tan(\alpha) + h \)
—
Les équations horaires sont x(t) et z(t) mais l’équation de la trajectoire est z(x) : le t a disparu !
—
On peut donc tracer la trajectoire dans un repère. En effet, on remarque que l’on a un polynôme du second degré, donc une parabole, tournée vers le bas car le coefficient du x2 est négatif. Et z(0) = h donc la parabole coupe l’axe des ordonnées en h :
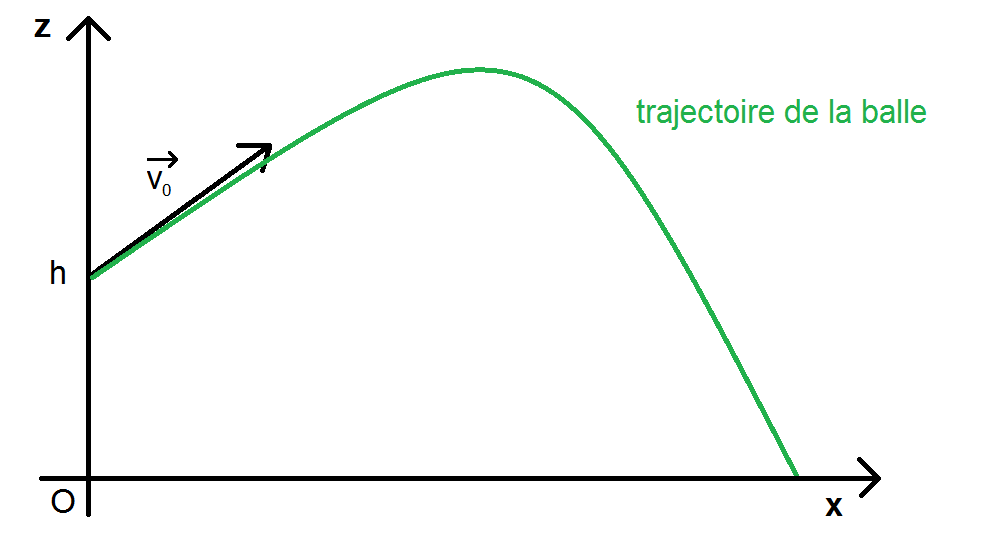
Cette trajectoire paraît plutôt logique, si on lance une balle vers le haut devant soi elle aura « à peu près » une trajectoire parabolique.
Cependant, la trajectoire ne sera pas exactement pareille dans la réalité, car on a négligé quelque chose… les frottements de l’air ! On en reparlera un peu plus loin.
Remarque : si tu dois tracer la trajectoire, fais en sorte qu’elle soit tangente au vecteur v0.
De même que dans l’exercice de la chute verticale, on peut te demander un certain nombre de choses à calculer.
Tout d’abord le sommet de la trajectoire, c’est-à-dire le point le plus haut atteint par l’objet. On peut calculer les deux coordonnées de ce point, que l’on notera xS et zS. Au niveau du schéma on a :
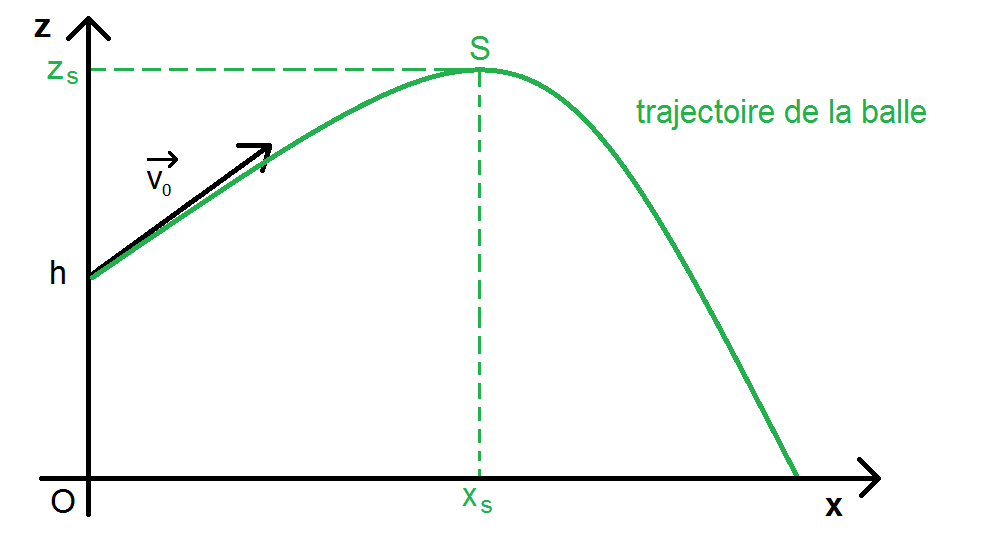
Pour ce faire deux solutions :
Tout d’abord, comme c’est une parabole dont on a l’équation, on peut calculer les coordonnées du sommet vues dans le chapitre sur les fonctions du second degré : il s’agit du α (le x) et du β (le z).
Ce calcul se fait à partir de l’équation de la trajectoire
\(\textstyle x_S = \frac{-b}{2a} \)
(le a est le coefficient de x2, pas le a de l’accélération…)
\(\displaystyle x_S = \frac{-tan(\alpha)}{\frac{-2g}{2v_0^2 cos^2(\alpha)}} \)
\(\displaystyle x_S = \frac{tan(\alpha) \times v_0^2 \times cos^2(\alpha)}{g} \)
(on pourra comme d’habitude vérifier que cette relation est bien homogène  )
)
Comme tan(α) = sin(α)/cos(α), on peut simplifier :
\(\textstyle x_S = \frac{sin(\alpha) \times v_0^2 \times cos(\alpha)}{g} \)
Maintenant qu’on a le x on remplace dans l’équation de la trajectoire pour trouver le zS :
\(\textstyle z_S = -g\frac{x_S^2}{2 v_0^2 cos^2(\alpha)} + x_S \times tan(\alpha) + h \)
On remplace ensuite avec l’expression de xS trouvée juste avant (mais on ne va pas le faire car l’expression est un peu longue à écrire  ).
).
Une fois que l’on a fait ça on peut remplacer les lettres par les valeurs données dans l’énoncé (sans oublier de convertir si besoin).
L’autre méthode pour trouver le sommet consiste à utiliser une particularité du sommet de la trajectoire. En effet, au sommet, la balle ne montera plus, donc LA VITESSE VERTICALE EST NULLE : vz = 0 m.s-1. On cherche alors le t noté tS :
\(\displaystyle v_Z = 0 \)
\(\displaystyle -gt + v_0 \times sin(alpha) = 0 \)
\(\displaystyle t_S = \frac{v_0 \times sin(\alpha)}{g} \)
Ce t correspond au temps mis par la balle pour arriver au sommet. Donc contrairement à la méthode précédente, on a en plus le temps au bout duquel la balle arrive au sommet.
On remplace alors t dans les équations horaires :
\(\textstyle \left\{ \begin{array}{c} x_S = v_0 \times cos(\alpha) \times t_S \\ z_S = -g\frac{t_S^2}{2} + v_0\times sin(\alpha) \times t_S + h \end{array} \right. \)
\(\textstyle \left\{ \begin{array}{c} x_S = \frac{v_0^2 \times cos(\alpha) \times sin(\alpha)}{g} \\ z_S = -g\frac{t_S^2}{2} + v_0\times sin(\alpha) \times t_S + h \end{array} \right. \)
Et là, oh magie !  on retrouve évidemment la même expression pour xS que précédemment. Ici encore on n’a pas remplacé dans le zS car l’expression est un peu longue, mais on trouverait la même chose qu’avant
on retrouve évidemment la même expression pour xS que précédemment. Ici encore on n’a pas remplacé dans le zS car l’expression est un peu longue, mais on trouverait la même chose qu’avant 
Ainsi, dans cette deuxième méthode tu n’auras pas à calculer l’équation de la trajectoire, mais tu devras calculer le temps t au bout duquel la balle atteint le sommet (du coup tu calcules en même temps cette durée, si elle est demandé dans l’énoncé ça fait deux questions de résolues^^), alors que dans la première méthode tu devais calculer l’équation de la trajectoire. Les deux méthodes se valent à toi de choisir celle que tu préfères !
On peut également te demander à quelle distance ou à quel moment va tomber la balle. Pour ce faire on va encore une fois utiliser une propriété de la situation : à l’endroit où va tomber la balle, on aura z = 0.
Par contre, on a 2 expressions pour z : z(x) et z(t) (équation de la trajectoire et équation horaire).
Si on demande à quelle distance va tomber la balle, on résout z(x) = 0.
Si on demande à quel moment va tomber la balle, on résout z(t) = 0.
Imaginons que l’on te demande à quel endroit tombe la balle : on résout donc z(x) = 0 :
\(\textstyle -g\frac{x^2}{2 v_0^2 cos^2(\alpha)} + x \times tan(\alpha) + h = 0 \)
On a donc une équation du second degré en x, donc il faut calculer delta, puis x1 et x2…
SAUF QUE vu les expressions des coefficients a, b et c, on va avoir un truc horrible !!!! 
A ce moment-là, EXCEPTIONNELLEMENT, on peut remplacer les lettres par les chiffres pour avoir une expression numérique de a, b et c et alors on peut calculer plus facilement delta, puis x1 et x2.
Parmi x1 et x2, il y en aura toujours un positif et un négatif (dans ce type d’exercices), et la distance que l’on cherche est bien sûr la positive. Cette distance correspond à la distance à laquelle tombera la balle.
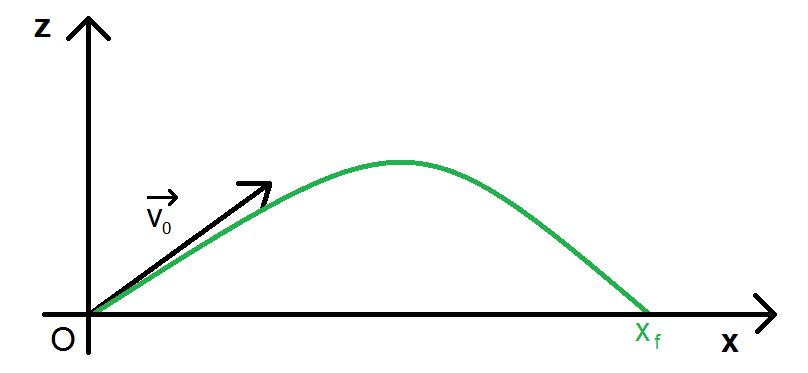
Ce genre de questions est plutôt rare, SAUF dans un cas particulier que nous allons étudier (et là tu vas voir que c’est beaucoup plus simple). Il s’agit du cas où h = 0, c’est-à-dire que la balle part de l’origine :
Absolument tout ce que l’on a fait avant est exactement pareil SAUF que l’on remplace h par 0 :
Résolvons alors z(x) = 0 comme précédemment pour trouver l’endroit où tombera la balle, noté xf :
\(\textstyle -g\frac{x^2}{2 v_0^2 cos^2(\alpha)} + x \times tan(\alpha) = 0 \)
Et là on peut factoriser par x :
\(\textstyle x \times (-g\frac{x}{2 v_0^2 cos^2(\alpha)} + tan(\alpha)) = 0 \)
Donc x = 0 ou (…) = 0, sauf que x = 0 correspond à l’origine, ce qui ne nous intéresse pas (mais ce qui est normal puisque à x = 0 on a bien z = 0 car la balle part de l’origine). On résout donc la parenthèse qui vaut 0 :
\(\displaystyle -g\frac{x_f}{2 v_0^2 cos^2(\alpha)} + tan(\alpha) = 0 \)
\(\displaystyle x_f = \frac{2 tan(\alpha) v_0^2 cos^2(\alpha)}{g} \)
\(\displaystyle x_f = \frac{2 sin(\alpha) v_0^2 cos(\alpha)}{g} \)
Et là on n’a pas eu besoin de faire le delta etc… car en factorisant on a pu se débarrasser de l’équation du second degré.
—
Remarque : à chaque fois dans ce type d’exercices on néglige les frottements. Donc en réalité la balle devrait arriver moins loin que la valeur trouvée avec l’expression précédente…
—
—
ATTENTION !! Tu remarqueras qu’à chaque fois (sauf pour l’équation du second degré ci-dessus) on n’a pas eu besoin des valeurs des différentes grandeurs. En effet, il faut trouver à chaque fois l’expression littérale (avec les lettres) ET SEULEMENT APRES remplacer par les valeurs pour l’application numérique.
Cela a déjà été dit dans d’autres chapitres mais dans ce type d’exercices c’est très important, car il y a des points pour l’expression littérale et des points pour l’application numérique. Si tu remplaces dès le début par les valeurs tu n’auras pas les points pour l’expression littérale.
—
—
De plus, en remplaçant dès le début par les valeurs, tu ne pourras pas vérifier l’homogénéité des formules.
En effet, seule l’expression littérale permet de vérifier l’homogénéité des formules et de détecter d’éventuelles erreurs (ce qui peut arriver dans ce chapitre vu les nombreux calculs à effectuer).
—
A force de faire ce genre d’exercices tu verras que c’est toujours la même chose à quelques différences près mais si tu as compris le principe général et tout ce qui a été expliqué dans ce chapitre tu ne devrais pas avoir de souci 
Tu peux t’entraîner sur les annales de bac il y a énormément de sujets comportant un exercice de ce genre.
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !



Merci beaucoup pour vos explications, je n’avais jamais rien compris de tout ce (charabia) mais je constate qu’il n’y avait rien de compliqué (●’◡’●).
Je comprenais rien au cour de mon prof. Incroyable j’ai tous compris maintenant!
À J-1 du bac vous me sauvez, merci beaucoup pour cette explication de qualité !!!
Demain j’ai un bac blanc en maths physique chimie etes équation horaires étai mon seul vrais point faible ces explications mon permis de très bien comprendre je relirais encore 2 3 fois le cours par sûreté
Merci
excellentes explications, merci beaucoup!
Merci beaucoup d’avoir pris le temps d’expliquer tout cela, c’est beaucoup plus clair pour moi maintenant!
Bonsoir, Merci infiniment pour votre explication incroyable, j’ai n’arrivais pas à comprendre cette chapitre ( c’était un peu compliqué pour moi ) mais là grâce à vous j’ai très bien compris. MERCI
Merci à toi 🙂
Vraiment votre explication est sincèrement claire et magnifique. C’est un travail de pédagogue rompu à la tâche. Coup de chapeau. Thanks.
Merci beaucoup ! 🙂
comment on sait que la primitives de t es égal t carré sur 2
je sais pas comment vous avez fait pour trouver ça ??
Regarde sur Méthode Maths le cours sur les primitives
Attention : dans la section Mouvement Parabolique, il y a une petite coquille pour l’expression de vz (le commentaire qui suit montre que c’est une coquille). Au cas où cela puisse éclaircir….
Merci pour ces excellents cours.
Merci beaucoup ! Erreur corrigée 🙂
Exelent pour les apprenants
Merci beaucoup.
Bonjour mercipour votre travail j’ai bien compris tout ce que vous avez expliqué sauf un point pourriez vous m’expliquer ce passage?
« Donc quand on projette le vecteur a, on a ax et az.
D’après ce qui précède le vecteur a est selon uz, donc ax = 0 et az = -g :
Si tu as bien suivi le chapitre précédent cela ne devrait pas te poser de problèmes »
Je n’arrive pas a comprendre pourquoi ax=0 et az=-g
Merci
Merci ! Les coordonnées du vecteur g sont (0 ; -g), c’est-à-dire 0 selon l’axe x et -g selon l’axe z, donc ax = 0 et az = -g (puisque le vecteur a est égal au vecteur g).
As-tu lu le chapitre précédent en question ?