Sommaire
Masse au bout d’un fil
Les montagnes russes
Masses-poulie avec frottements
Puits de potentiel infini
N’hésite pas à aller d’abord voir le cours sur l’énergie en mécanique avant de faire les exercices 
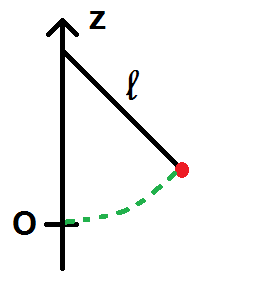
On dispose d’un objet de masse m au bout d’un fil de longueur l, ce fil est fixé en un point de l’axe (Oz) à une certaine hauteur de sorte que la masse passera par l’origine du repère lors de son mouvement. Ce mouvement s’effectue sans frottement.
Initialement, le fil fait un angle α avec l’axe vertical et la masse est lâchée sans vitesse initiale. La position initiale est notée A.
On prend l’origine de l’énergie potentielle de pesanteur au niveau de l’origine O de l’axe vertical.
1) Le schéma est donné ci-dessous mais il est incomplet : compléter le schéma.
2) Calculer la vitesse de l’objet quand il passera à l’origine de l’axe vertical (donc en O).
3) Même question en prenant l’origine de l’axe au point de fixation du fil, l’origine de l’énergie potentielle de pesanteur étant toujours au niveau de l’origine O (donc au point de fixation du fil).
Une bille glisse sans frottement (frottements négligés) sur une surface ayant la forme du schéma ci-dessous (des montagnes russes).
La bille est initialement en A. Le premier sommet rencontré est noté B.
L’énergie potentielle de pesanteur est prise nulle à l’origine O de l’axe vertical (Oz).
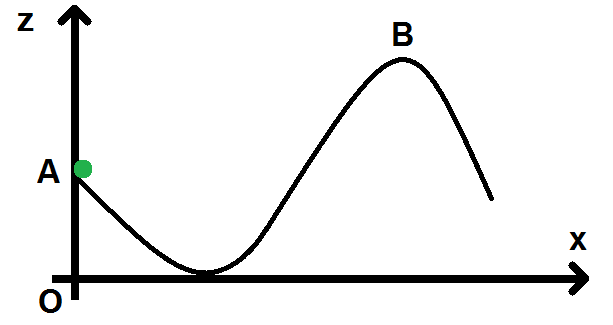
1) Exprimer en fonction de g, zB et zA la vitesse minimale VA min à communiquer à la balle en A pour atteindre le sommet B.
2) On prend vA = 5,0 m.s-1, zA = 2,0 m et g = 10 m.s-2.
Quelle hauteur maximale notée zmax la bille peut-elle atteindre ?
On considère deux masses m et M reliés par un fil inextensible posé sur une poulie.
On note μd le coefficient de frottement entre la masse m et le plan sur lequel elle repose.
On obtient la schéma suivant :
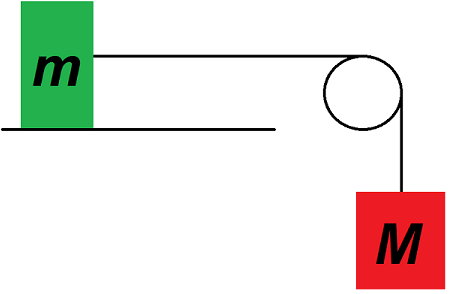
1) Trouver la masse nécessaire M pour que le système se mette mouvement.
2) On suppose maintenant que la masse M vérifie la condition trouvée au 1), et on la lâche d’une hauteur h du sol.
A la fin du mouvement, la masse m s’est décalée vers la droite d’une longueur h + d.
Exprimer μd en fonction des données de l’énoncé (m, M, h et d).
Le puits de potentiel infini est un exercice classique de la mécanique quantique, c’est une application directe de l’équation de Schrödinger.
On considère un axe horizontal (Ox), avec un potentiel nul pour x compris entre 0 et L, et infini ailleurs (donc x < 0 et x > L).
Déterminer la fonction d’onde Ψ pour tout x.


