L’effet DOPPLER

Sommaire

Introduction
Principe général : formules
Interprétation : graves et aigus
Démonstration
Exercices

Introduction
L’effet DOPPLER (du nom de celui que l’Histoire a retenu comme celui qui l’a théorisé) apparaît quand une onde est émise et qu’elle est reçue par un récepteur mais que la distance entre l’émetteur et le récepteur n’est pas fixe.
Il s’agit par exemple de la sirène d’un camion de pompiers : le camion est en mouvement par rapport à toi, et tu n’entends pas la sirène de la même manière suivant que le camion se rapproche ou s’éloigne de toi : c’est l’effet DOPPLER.
Dans ce chapitre nous verrons les formules qui permettent de caractériser ce phénomène.
En réalité il n’y a qu’une seule formule générale mais qui s’applique à 4 situations différentes : nous ferons donc la démonstration de la formule dans 1 des situations car elle peut t’être demandée en contrôle. En effet, à part la formule on ne peut pas te demander grand chose dans ce chapitre puisqu’il n’y a qu’une seule formule…
Ce chapitre va faire intervenir des notions vues dans le chapitre sur les ondes, il est donc conseillé de le relire auparavant

Principe général : formules

Haut de page

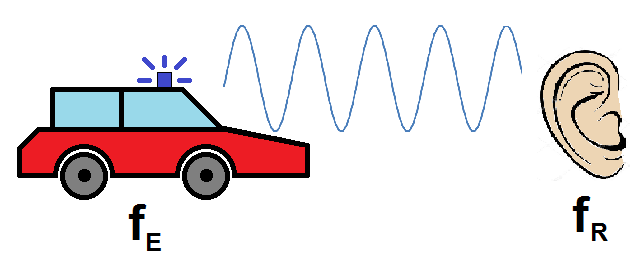
Le principe va être le suivant : on a un émetteur (on va prendre un véhicule avec une sirène) qui émet une onde.
Cette onde émise a une fréquence notée f_E (E pour émetteur).
Le récepteur (modélisé par une oreille) reçoit cette onde et la perçoit avec une fréquence f_R (R pour récepteur).
Si l’émetteur et le récepteur sont immobiles l’un par rapport à l’autre, f_R = f_E : il n’y a pas d’effet DOPPLER.

Il y a donc forcément un mouvement de l’un par rapport à l’autre.
On peut avoir quatre cas :
– l’émetteur se rapproche du récepteur ;
– l’émetteur s’éloigne du récepteur ;
– le récepteur se rapproche de l’émetteur ;
– le récepteur s’éloigne de l’émetteur.

Tu pourrais te dire que le fait que le récepteur se rapproche de l’émetteur ou que l’émetteur se rapproche du récepteur revient au même. Nous verrons que non…

Dans chacun des quatre cas on suppose que l’émetteur ou le récepteur est en mouvement mais que l’autre est immobile.
On peut très bien combiner en disant que le récepteur s’éloigne et que l’émetteur s’éloigne aussi par exemple : nous verrons que cela est compris dans la formule générale (même si ce genre de cas n’est pas étudié au lycée).

Dans tous les cas, la vitesse de déplacement du récepteur ou de l’émetteur sera nécessairement constante.

La vitesse du récepteur sera noté v_R, et celle de l’émetteur v_E.
v_R et v_E sont nécessairement positifs, qu’ils s’éloignent ou qu’ils se rapprochent.
La distinction entre éloignement et rapprochement se fera dans la formule avec des + et des -.

Les 4 situations sont représentés sur le schéma suivant :

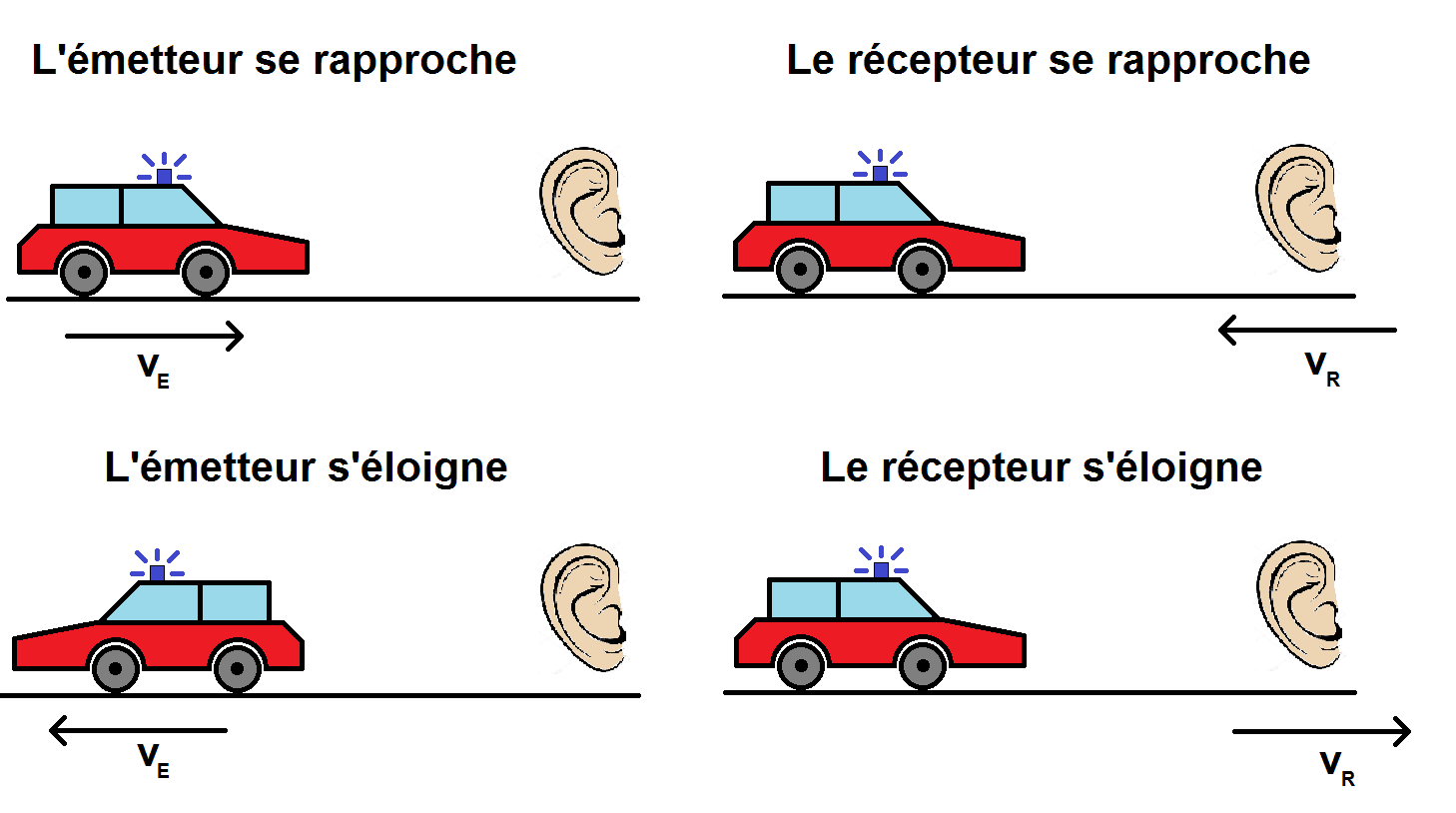
Il y a alors une formule générale qui lie les fréquences et les vitesses du récepteur.
En notant c la vitesse de l’onde, on a :

Dans cette formule :
f_E est la fréquence de l’onde émise, en Hz
f_R est la fréquence de l’onde reçue, en Hz
v_E est la vitesse de l’émetteur, en m.s^-1
v_R est la vitesse du récepteur, en m.s^-1
c est la vitesse de l’onde émise, en m.s^-1 (pour une onde sonore on a c = 340 m.s^-1).

—
Remarque : si l’émetteur est immobile, on prend v_E = 0 m.s^-1
Si le récepteur est immobile, on prend v_R = 0 m.s^-1
—

Tu as sûrement dû remarquer les signes ± (plus ou moins) au numérateur et au dénominateur.
En fait on va choisir + ou – suivant que l’émetteur ou le récepteur s’éloigne ou se rapproche.

La seule difficulté de ce chapitre réside dans le fait qu’il faut se souvenir par cœur des règles qui suivent :
– au numérateur : + si le récepteur se rapproche, – si le récepteur s’éloigne
– au dénominateur : + si l’émetteur s’éloigne, – si l’émetteur se rapproche.

Comme tu le vois la règle n’est pas la même pour le numérateur et le dénominateur, d’où la difficulté !!

Nous t’avons mis ça sur le schéma pour que tu aies un moyen visuel de t’en souvenir :

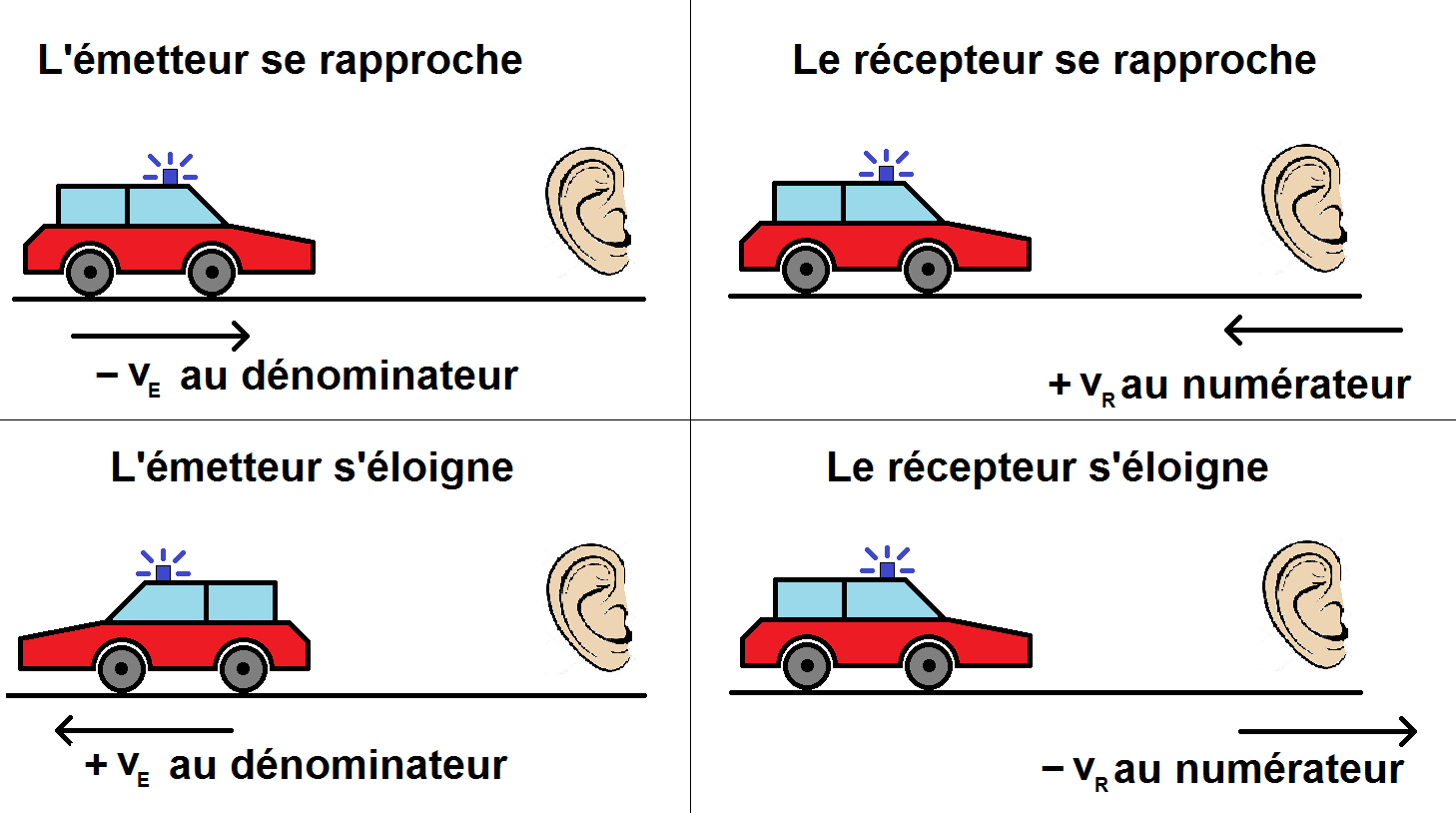
On peut donc avoir les formules suivantes :

Bien sûr on peut tout à fait combiner 2 règles si l’émetteur ET le récepteur sont en mouvement.
Si par exemple on a l’émetteur qui se rapproche (- v_E) et le récepteur qui se rapproche (+ v_R), on a :

Cela donne donc plein de possibilités, mais tu n’as que deux choses à retenir : la formule générale, et les règles qui permettent de savoir si c’est + ou – (tu peux retenir avec le schéma, surtout si tu as une mémoire visuelle).

Dans les exercices, on te donnera toutes les valeurs de la formule sauf une et tu devras calculer cette valeur grâce à la formule (nous verrons cela dans les exercices).
Evidemment il faudra au préalable avoir donné la bonne formule en se basant sur ce qui est dit dans l’énoncé.

Interprétation : graves et aigus

Haut de page

Nous allons voir que la formule va nous donner une indication sur la perception que l’on a du son (donc au niveau du récepteur).
On rappelle tout d’abord que plus la fréquence est faible, plus le son est grave, plus la fréquence est élevée plus le son est aigu.

Supposons que l’émetteur se rapproche du récepteur ou que le récepteur se rapproche de l’émetteur (dans les 2 cas il y a rapprochement de l’émetteur et du récepteur).
D’après ce que l’on vient de voir, on a une des deux formules suivantes :

Dans la première formule, c + v_R > c donc (c + v_R)/c > 1 donc f_R > f_E
Dans la deuxième formule, c > c – v_E donc c/(c – v_E) > 1 donc f_R > f_E
Dans les deux cas f_R > f_E

Donc le récepteur perçoit un son plus aigu que le son émis !!
Ainsi, si dans la rue un camion de pompiers se rapproche vers toi, tu entendras une sirène plus aiguë que la sirène émise par le camion.

—
Dans le cas d’un rapprochement entre l’émetteur et le récepteur, le son perçu est plus aigu que le son émis car la fréquence reçue est plus élevée.
—

A l’inverse, si l’émetteur et le récepteur s’éloignent, on a une des deux formules :

Dans la première formule, c – v_R < c donc (c – v_R)/c < 1 donc f_R < f_E
Dans la deuxième formule, c < c + v_E donc c/(c + v_E) < 1 donc f_R < f_E
Dans les deux cas f_R < f_E

Le récepteur perçoit donc un son plus grave que celui émis.
Donc quand le camion de pompiers sera passé devant toi et s’éloignera, tu percevras une sirène plus grave que celle émise, et donc plus grave que celle que tu entendais quand il se rapprochait (tu feras le test la prochaine que ça t’arrivera dans la rue )

—
Dans le cas d’un éloignement entre l’émetteur et le récepteur, le son perçu est plus grave que le son émis car la fréquence reçue est plus faible.
—

Pour expliquer cela, tu es invité à regarder l’animation au début cette page Wikipédia dont on a extrait l’image suivante :

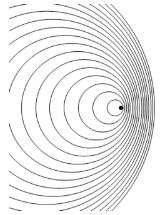
Ici l’émetteur va vers la droite : si le récepteur est à droite (donc rapprochement) on voit que la distance entre deux ondes reçues est très faible : cette distance correspond à la longueur d’onde λ (comme vu dans le chapitre sur les ondes)
Or on sait que c = λ × f donc f = c/λ : plus λ est faible, plus f est élevée.
Ainsi dans le cas d’un rapprochement la fréquence reçue est plus élevée : cela correspond à ce que l’on a vu précédemment ! (heureusement )

A l’inverse, si le récepteur est à gauche (donc éloignement), on voit que la distance entre deux ondes reçues est plus élevée : donc λ est plus grand donc f est plus faible.
Donc dans le cas d’un éloignement la fréquence reçue est plus faible : cela correspond évidemment à ce que l’on a vu précédemment

On peut donc retenir la chose suivante :

—
Dans le cas d’un rapprochement entre l’émetteur et le récepteur, f_R > f_E
Dans le cas d’un éloignement entre l’émetteur et le récepteur, f_R < f_E
—

Cela peut être un bon moyen mnémotechnique pour se souvenir des cas où l’on met + ou – dans la formule générale.

Démonstration

Haut de page

Nous allons à présent démontrer la formule dans un des cas évoqués ci-dessus.
Souvent les exercices que tu auras à faire sur ce chapitre seront les démonstrations mais qui seront données sous forme d’exercice avec des questions intermédiaires. La démonstration qui suit n’est donc donc pas à apprendre par cœur mais il est préférable de bien la maîtriser quand même

Nous allons faire le cas où l’émetteur se rapproche du récepteur, ce dernier étant fixe.
On rappelle tout d’abord que la fréquence d’une onde est reliée à la période par la formule :

Dans la démonstration, pour calculer f_R on va calculer T_R qui correspond à la durée entre deux ondes reçues. On va donc regarder à quel moment la première onde émise est reçue et à quel moment la deuxième onde émise est reçue. Le temps entre ces deux moment correspondra à T_R.
De la même manière, l’instant entre la première et la deuxième onde émise sera égale à T_E. La 1ère onde étant émise à t = 0s, la 2ème onde sera émise à t = T_E = 1/f_E.

Par ailleurs, la vitesse de l’émetteur étant constante, on peut utiliser la formule :

On pourra faire de même avec l’onde qui a une vitesse constante notée c.

On prend un axe horizontal (0x), l’émetteur étant à l’origine O de cet axe à t = 0s.
On suppose par ailleurs qu’initialement l’émetteur et le récepteur sont séparés d’une distance D.

A t = 0s, l’émetteur émet une onde (dont la vitesse est c).

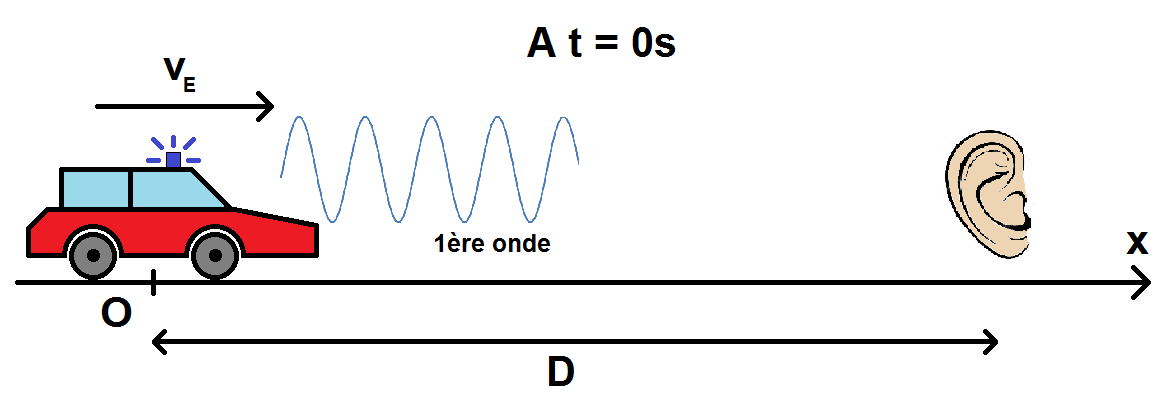
L’onde doit parcourir la distance D pour être reçue par le récepteur.
Elle sera donc entendue à l’instant t₁ défini par :

Pendant ce temps l’émetteur avance vers le récepteur et va émettre une deuxième onde à l’instant t₂ = 1/f_E (d’après ce qui a été dit précédemment).
A cet instant, l’émetteur (qui va à la vitesse v_E) aura parcouru une distance d₂ :

On a alors le schéma suivant :

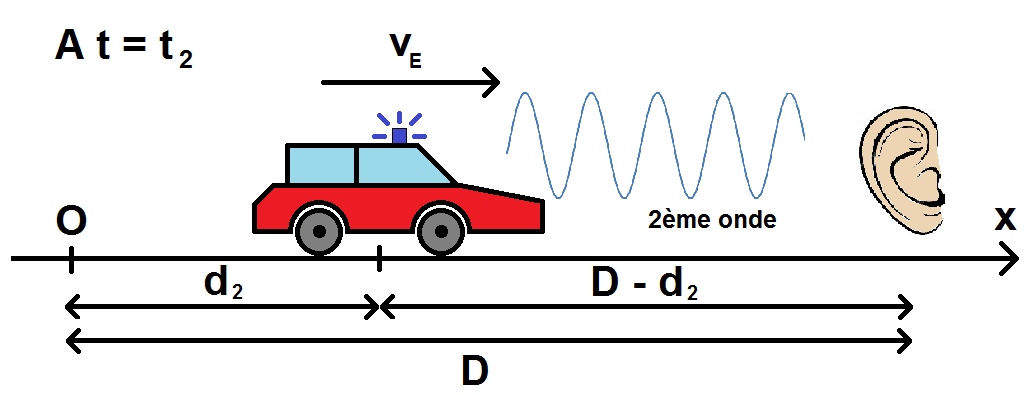
A cet instant t₂ l’émetteur émet une deuxième onde qui va devoir parcourir la distance D – d₂ avant d’arriver au récepteur. On appelle t₃ le moment où l’onde arrive au récepteur.
L’onde allant à la vitesse c, on a :

—
ATTENTION à ne pas oublier le t₂ à ce niveau-là de la démonstration !!
En effet, (D-d₂)/c représente le temps mis par l’onde pour parcourir D-d₂, mais il ne faut pas oublier que l’onde à été émise à l’instant t₂…
Très souvent les élèves oublient le t₂ à ce moment-là car ils pensent uniquement à la formule t = d/v sans penser que cette deuxième onde a été émise à l’instant t₂.
—

Ainsi, le récepteur a reçu la première onde à l’instant t₁ et la deuxième onde à l’instant t₃.
La période de l’onde reçue est donc :

Or on a vu que t₂ = 1/f_E

En simplifiant D/c on obtient :

Or d₂ = v_E/f_E, donc :

On met au même dénominateur et on remplace T_R par 1/f_R

En inversant tout on obtient :

Or on avait vu que quand l’émetteur se rapprochait on avait – v_E au dénominateur : CQFD !

Comme tu le vois ce n’est pas une démonstration très simple car il y a plein de variables à prendre en compte (t₁, t₂, d₂ etc…), ce pourquoi faire des schémas comme ci-dessus aide beaucoup à comprendre.
Tu vois également qu’il vaut mieux avoir déjà vu une fois cette démonstration plutôt que de la découvrir le jour du contrôle, ne serait-ce que pour éviter les pièges (notamment l’histoire du t₂ à ajouter au t₃…).

De plus, il faut faire attention quand tu utilises la formule v=d/t à bien mettre la bonne vitesse : si on parle de l’émetteur il faut mettre v_E, si on parle de l’onde il faut mettre c, si on parle du récepteur il faut mettre v_R.

Entraîne-toi à refaire cette démonstration avec les autres cas (émetteur qui s’éloigne etc…) afin de voir si tu retrouves bien les bonnes formules, tu verras ainsi si tu as bien compris le raisonnement .

Exercices

Haut de page

Les exercices seront bientôt disponibles !

Sommaire des coursHaut de la page