Les dosages – titrages

Sommaire

Introduction
Principe général – schéma
Dosage par colorimétrie
Dosage pH-métrique
Indicateur coloré
Dosage par conductimétrie
Propriétés de la réaction de dosage
Piège à éviter
Exercices

Introduction

Nous allons voir dans ce chapitre les dosages par titrage.
Doser une solution, cela signifie déterminer sa concentration. Nous allons donc doser des solutions dont on ne connaît pas la concentration.
Le titrage est une des méthodes pour doser une solution, on parle donc de dosage par titrage.

Nous verrons le principe du dosage avec le vocabulaire spécifique, mais aussi le schéma qui pourra t’être demandé en contrôle ou en TP, puisque tu peux avoir des dosages à l’épreuve de TP au Bac.

Principe général

Le dosage par titrage repose sur une équation chimique qui va faire intervenir deux solutions.
La première est la solution titrée, qui est la solution de concentration inconnue.
La deuxième est la solution titrante, qui est une autre solution mais dont on connaît la concentration.

Souvent chacune de ces solutions est composée de deux espèces, et une seule des deux espèces de chaque solution va intervenir dans l’équation de la réaction. Les autres espèces présentes seront spectatrices.

Exemple : on dose une solution d’acide chlorhydrique H₃O⁺ + Cl^– par une solution d’hydroxyde de sodium HO^– + Na⁺.
Ici ce sont les ions H₃O⁺ qui vont réagir avec les ions HO^– selon l’équation :
H₃O⁺ + HO^– → 2 H₂O
Les ions Cl^– et Na⁺ sont des ions spectateurs.

Evidemment il y aura des indications dans l’énoncé pour t’indiquer qui réagit avec qui.

Dans cet exemple, qui est la solution titrante et qui est la solution titrée ??
C’est très simple, l’acide chlorhydrique est la solution titrée car on dit qu’on la dose, c’est donc la concentration de cette solution que l’on cherche. L’hydroxyde de sodium est donc la solution titrante.

Mais on ne va pas mélanger ces deux solutions ensemble dès le début !
En effet, ce n’est pas un protocole habituel pour un dosage : la solution titrée sera dans un bécher dès le début de la réaction, elle aura donc un volume fixe.
En revanche, la solution titrante sera dans une burette graduée au-dessus du bécher, et on va rajouter progressivement cette solution dans le bécher.
On aura donc le schéma suivant :

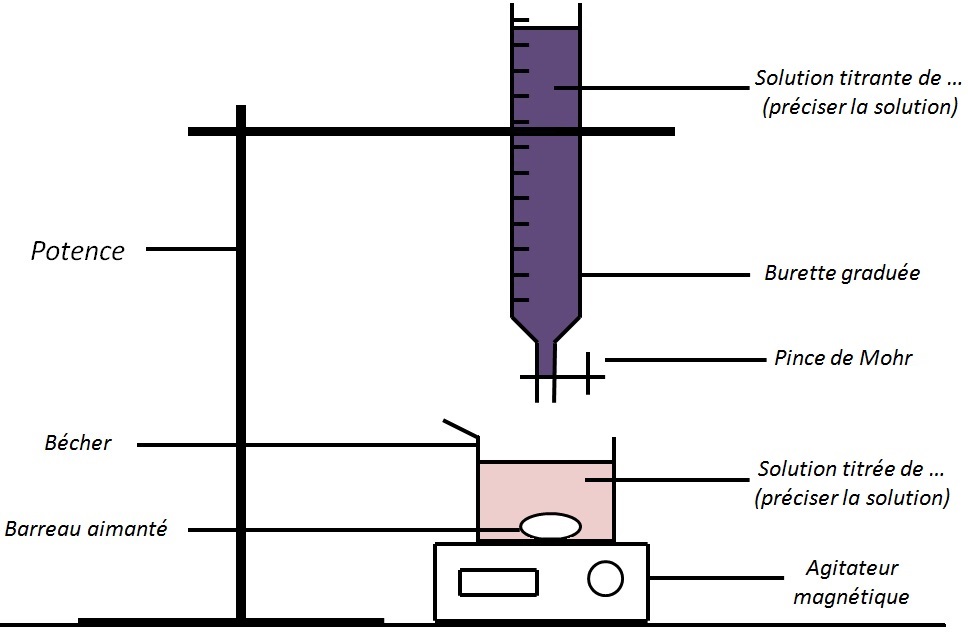
Ce schéma est évidemment à connaître par cœur !!!
Sachant qu’il s’agit ici du schéma de base, si on fait un dosage pH-métrique ou conductimétrique il faut rajouter une sonde avec l’appareil correspondant.
Tout cela est détaillé dans la vidéo ci-dessous, les schémas sont volontairement simples afin que tu puisses les reproduire facilement sur ta copie !

Comme tu le vois, au début de la réaction, seule la solution titrée se trouve dans le bécher (dans le milieu réactionnel).
Le principe du titrage va être le suivant :
– on va rajouter progressivement la solution titrante en appuyant sur la pince de Mohr
– ce que l’on rajoute dans le bécher va réagir, il va donc se former des produits, mais la quantité de solution titrée va diminuer puisque c’est un réactif (bien remarquer que la quantité de l’espèce de la solution titrante qui intervient dans la réaction est nulle dans le milieu réactionnel car tout ce que l’on ajoute réagit automatiquement)
– au bout d’une certaine quantité ajoutée, toute la solution titrée aura réagi : c’est ce qu’on appelle l’équivalence
– si on continue à rajouter de la solution titrante, il n’y aura plus de réaction puisqu’il n’y aura plus de solution titrée pour réagir : la quantité de matière des produits restera constante et seule la quantité de solution titrante augmentera.

A l’équivalence, toute la solution titrée a réagi : il n’y en a plus. Mais il n’y a pas non plus de solution titrante car tout ce que l’on a ajouté a réagi !
Ainsi il n’y a plus de réactif dans le mélange réactionnel à l’équivalence, que des produits : on dit alors que les réactifs ont été introduits dans les proportions stœchiométriques !

—
L’équivalence correspond au moment où les réactifs titrant et titré ont été introduits dans les proportions stœchiométriques.
—

Retiens bien cette définition par cœur car elle souvent demandée en contrôle, et très souvent au Bac !! Ce sont des points gagnés facilement

Remarque : il n’y a plus de réactif mais les ions spectateurs sont toujours présents puisqu’ils n’ont pas réagi… nous verrons que cela est important dans les dosages par conductimètre notamment.

Tout cela peut être résumé sous forme de tableau d’un tableau d’avancement, qu’il faut là encore savoir impérativement refaire car dès qu’il y a un titrage il faut faire le tableau d’avancement de la réaction !!
Supposons que l’on appelle A la solution titrée et B la solution titrante.
D’après ce qui précède, au début de la réaction il n’y a pas de B dans le milieu réactionnel mais une certaine quantité n_A de solution titrée.
On va distinguer 4 phases différentes :
– état initial
– avant l’équivalence (il y a du A mais il n’y a pas de B)
– à l’équivalence (il n’y a ni A ni B)
– après l’équivalence (il y a du B mais il n’y a plus de A)

On suppose que l’équation de la réaction est aA + bB → cC + dD (a, b c et d sont les coefficients stœchiométriques).
A l’équivalence, l’avancement est noté x_E

—
ATTENTION !! Pour un dosage il n’y a ni x_f ni x_max mais x (avant l’équivalence) et x_E (à l’équivalance et après l’équivalence).
—

Cela donne le tableau suivant :

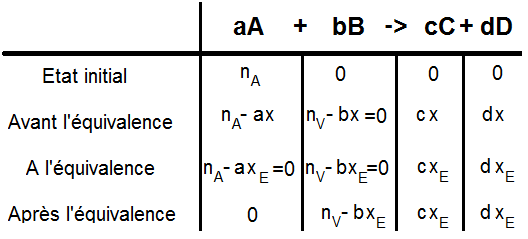
Plusieurs remarques :
– la quantité de matière de B est notée n_V comme n_versée, car le B est versé au fur et à mesure.
– n_V varie au cours du temps : en effet n_V = C_B x V_versé (en notant V_versé le volume de B versé) : comme V_versé augmente, n_V augmente.
– Avant l’équivalence, comme tout le B versé est consommé, on a mis = 0 mais ce n’est pas une obligation, c’est plus une aide à la compréhension.
– De même à l’équivalence on a mis = 0 pour A et B mais ce n’est pas obligatoire.
– Après l’équivalence, comme il n’y a plus de réaction puisqu’il n’y a plus de A, le x reste x_E : la quantité de C et D reste constante mais celle de B augmente (puisque n_V augmente mais que x_E reste constant).

A l’équivalence, le volume versé sera noté V_E : V_v = V_E à l’équivalence.

Nous allons voir maintenant comment utiliser le tableau pour trouver la concentration inconnue (car le dosage sert à ça !).

Pour cela, il faut se placer à l’équivalence.
On sait qu’à l’équivalence :

d’où :

Ainsi :

Or on sait que n = C x V, avec V_v = V_E puisque l’on est à l’équivalence, donc :

On isole ensuite C_A puisque c’est ce que l’on cherche :

Il ne reste plus qu’à remplacer avec les données de l’énoncé !
Très souvent on aura a = 1 et b = 1 ce qui simplifiera les expressions.

Ainsi, comme on connaît C_B, V_A et V_E que l’on a déterminé, on peut calculer la concentration C_A que l’on cherche.

Mais comment déterminer le volume équivalent V_E ? Tout dépend du type de dosage.

Dosage par colorimétrie

Haut de page

Il existe trois principaux types de dosage :
– le dosage par colorimétrie
– le dosage par suivi pH-métrique
– le dosage par conductimétrie

Nous allons les étudier un par un. Commençons par le dosage colorimétrique (le plus simple) aussi appelé dosage par colorimétrie.

Le dosage par colorimétrie consiste, comme son nom l’indique, à repérer l’équivalence grâce au changement de couleur de la solution.
Il faut donc que la solution titrante ou titrée (ou les 2) soient colorées.

– Supposons que la solution titrée soit la seule colorée, la titrante et les produits étant incolores.
Avant l’équivalence, la solution sera colorée puisqu’il reste de la solution titrée.
A l’équivalence, la solution est incolore puisqu’il n’y a plus de solution titrée.
Il en est de même après l’équivalence.

L’équivalence correspond donc à l’instant où la solution devient incolore !
Ainsi, on verse goutte à goutte la solution titrante tant que la solution est colorée, et dès qu’elle devient incolore on s’arrête car on a atteint l’équivalence : on regarde alors le volume versé qui correspond à V_E.

– Supposons maintenant que la solution titrante soit la seule colorée, la titrée et les produits étant incolores.
Avant l’équivalence, la solution sera incolore puisque toute la solution titrante versée est consommée.
A l’équivalence, la solution est incolore puisqu’il n’y a pas de solution titrante.
Après l’équivalence, la solution sera colorée puisqu’il y aura de la solution titrante.

L’équivalence correspond donc à l’instant où la solution devient colorée !
Ainsi, on verse goutte à goutte la solution titrante tant que la solution est incolore, et dès qu’elle devient colorée on s’arrête car on a atteint l’équivalence : on regarde alors le volume versé qui correspond à V_E.

– Supposons maintenant que les solutions titrante et titrée soient colorées, les produits étant incolores.
Avant l’équivalence, la solution sera de la couleur de la solution titrée.
A l’équivalence, la solution est incolore puisqu’il n’y a pas de solution ni titrante ni titrée (il n’y a que les produits qui sont incolores).
Après l’équivalence, la solution sera de la couleur de la solution titrante.

Encore une fois l’équivalence sera repérée par le changement de couleur.

Le problème de cette technique est qu’elle n’est pas très précise, et qu’il est difficile de faire un graphique contrairement aux deux autres méthodes, ce pourquoi en contrôle on aura plus souvent les deux autres types de titrage.

Dosage pH-métrique

Haut de page

Le dosage pH-métrique est un dosage où l’on suit l’évolution du pH au cours de la réaction.
Comme on l’a vu précédemment, il faudra ajouter une sonde pH-métrique avec un pH-mètre pour relever le pH en fonction du volume versé, ce qui donne le schéma suivant :

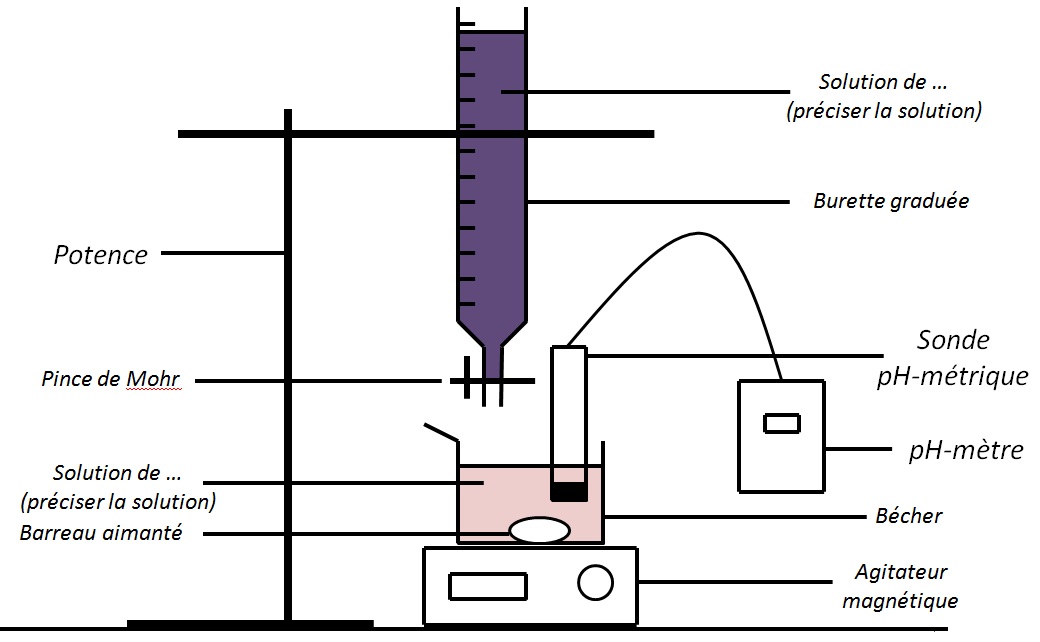
Il faut que le pH varie beaucoup, ce pourquoi la réaction de dosage sera une réaction acido-basique.

Pour suivre l’évolution du pH, on remplira ce genre de tableau :

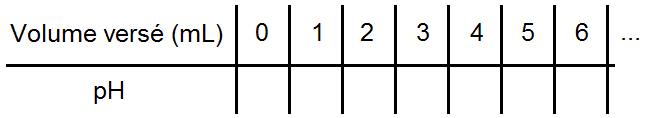
A partir de ce tableau on va pouvoir tracer une courbe représentant le pH en fonction du volume versé (le volume en abscisse et le pH en ordonnée) :

Comme on le voit, le pH varie fortement à un moment : c’est l’équivalence.
Mais le volume équivalent n’est pas déterminé pour autant !
Pour cela, on applique ce que l’on appelle la méthode des tangentes.

Pour te l’expliquer une petite vidéo va te montrer toutes les étapes de cette méthode :

Le problème de cette méthode est qu’elle n’est pas très précise, notamment à cause du tracé des tangentes qui n’est pas précis.
C’est pourquoi il arrive qu’en contrôle, et en particulier au bac, on te propose une deuxième méthode qui utilise la dérivée.
Grâce à un logiciel de calcul, l’ordinateur fournit automatiquement la dérivée de la courbe précédente, on obtient une courbe qui ressemble à ça :

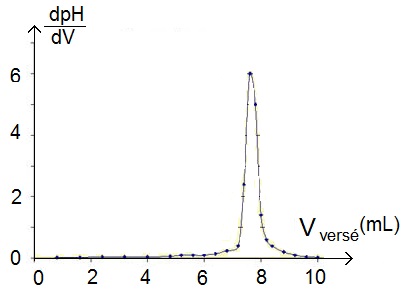
Remarque : le dpH/dV en ordonnée signifie bien que l’on a la dérivée de la courbe du pH en fonction du volume.

La méthode est alors beaucoup plus simple puisqu’il suffit de regarder le maximum de cette courbe et de regarder le volume correspondant, qui correspond au volume équivalent !

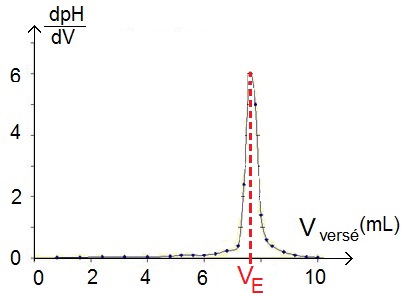
Cette méthode a en plus l’avantage d’être plus précise.

Dans les contrôles, et en particulier au Bac, on te donne plutôt les 2 courbes sur le même graphique et on te demande de déterminer le volume équivalent par la méthode de ton choix (donc soit la méthode des tangentes, soit cette 2ème méthode avec la dérivée).
Evidemment tu choisiras la 2ème méthode qui est beaucoup plus simple et précise

Voici par exemple le graphe donnée au Bac Antilles Guyane en 2013 :

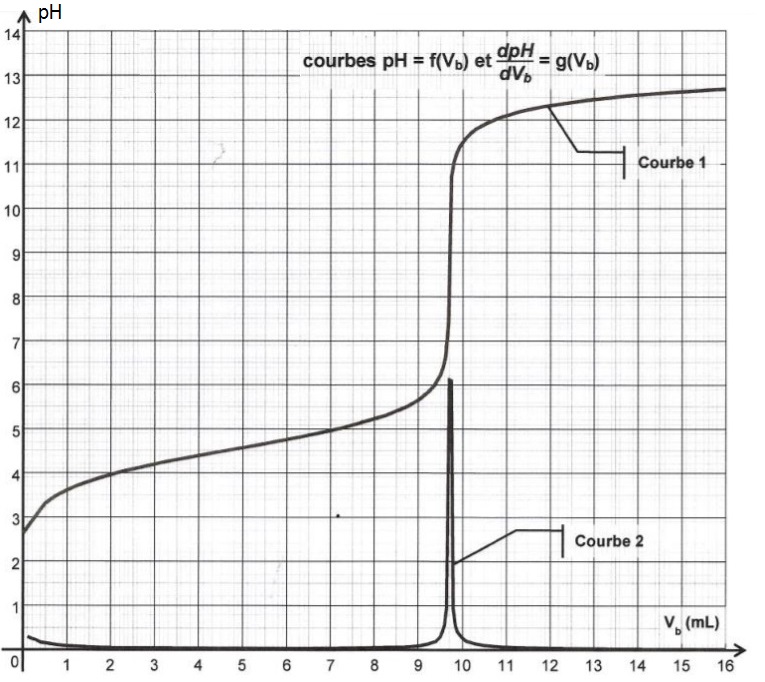
Les question étaient :
– Parmi les courbes 1 et 2, quelle est celle qui représente pH = f(Vb) et celle qui représente dpH/dV= g(Vb) ? Justifier.
– Déterminer la valeur du volume équivalent V_E par une méthode de votre choix.

Comme tu le vois c’est très simple !

Et voici la courbe donnée au Bac en Polynésie en 2014 :

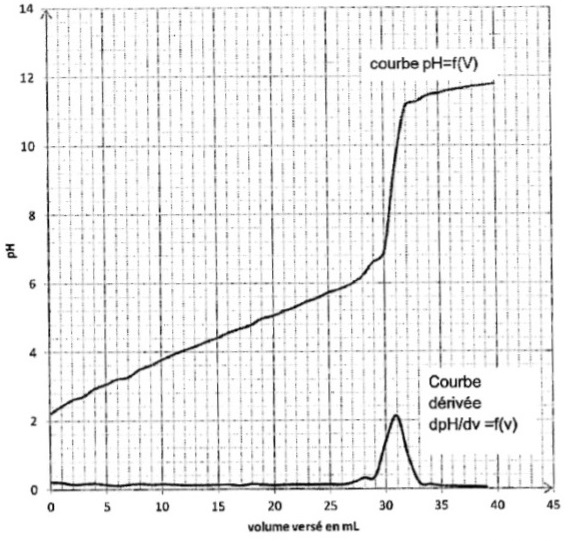
Là encore les questions étaient les mêmes, et comme tu vois les deux courbes sont données sur le même graphe.

Indicateur coloré

Haut de page

Avant de voir le dernier type de dosage, nous allons parler des indicateurs colorés.

Un indicateur coloré acido-basique correspond à un couple acide-base dont les formes acides et basiques ont des couleurs différentes.
Suivant le pH du milieu dans lequel l’indicateur va se trouver, la forme acide ou la forme basique va prédominer et donc la couleur sera différente.
Par exemple : la forme acide du couple sera verte et la forme basique sera jaune.

Chaque indicateur coloré possède ce que l’on appelle une zone de virage, qui correspond à un intervalle de pH où la couleur va changer. Exemple :

Dans les dosages, on peut rajouter un indicateur coloré afin d’aider à repérer l’équivalence.
Pour cela, il faut que le pH à l’équivalence appartienne à la zone de virage !

Prenons l’exemple précédent :

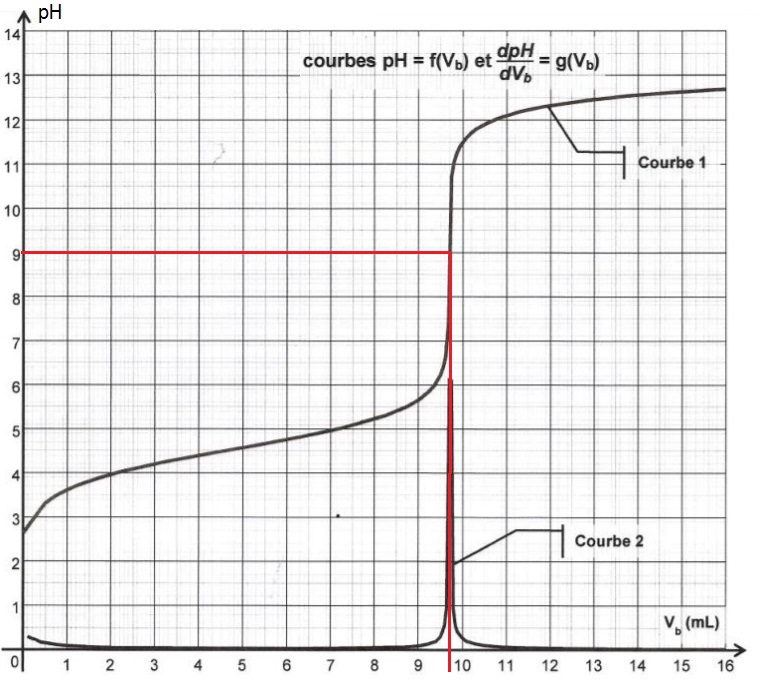
Comme on le voit, le pH à l’équivalence est de 9.
La question posée était de choisir l’indicateur coloré le mieux adapté parmi les 3 du tableau ci-dessus : il faut répondre la phénolphtaléine, car sa zone de virage est 8,2 – 10, et 9 appartient bien à cet intervalle.
En revanche, 9 n’appartient pas aux zones de virage des autres indicateurs colorés donc ils ne conviennent pas.

Comme tu le vois ce sont des points gagnés facilement !

—
Ce que tu dois retenir, c’est que le pH à l’équivalence doit appartenir à la zone de virage de l’indicateur coloré choisi.
—

Mais à quoi sert cet indicateur coloré ?
Il aide à repérer l’équivalence : en effet, quand la solution commence à changer de couleur, c’est que le pH à l’équivalence est proche : on peut donc être plus précis dans la solution versée afin d’avoir plus de points : on peut par exemple verser non pas mL par mL mais plutôt par 0,5 mL pour avoir deux fois plus de points par exemple.

Evidemment il faut que la solution de base (sans l’indicateur coloré) soit incolore sinon les couleurs vont se mélanger et cela n’aurait aucune utilité.

Passons maintenant au dernier type de dosage !

Dosage par conductimétrie

Haut de page

Le dosage par conductimétrie (ou conductimétrique) est un dosage où l’on suit l’évolution de la conductivité σ (sigma) de la solution au cours de la réaction.
Comme on l’a vu précédemment, il faudra ajouter une sonde conductimétrique avec un conductimètre pour relever σ en fonction du volume versé, ce qui donne le schéma suivant :

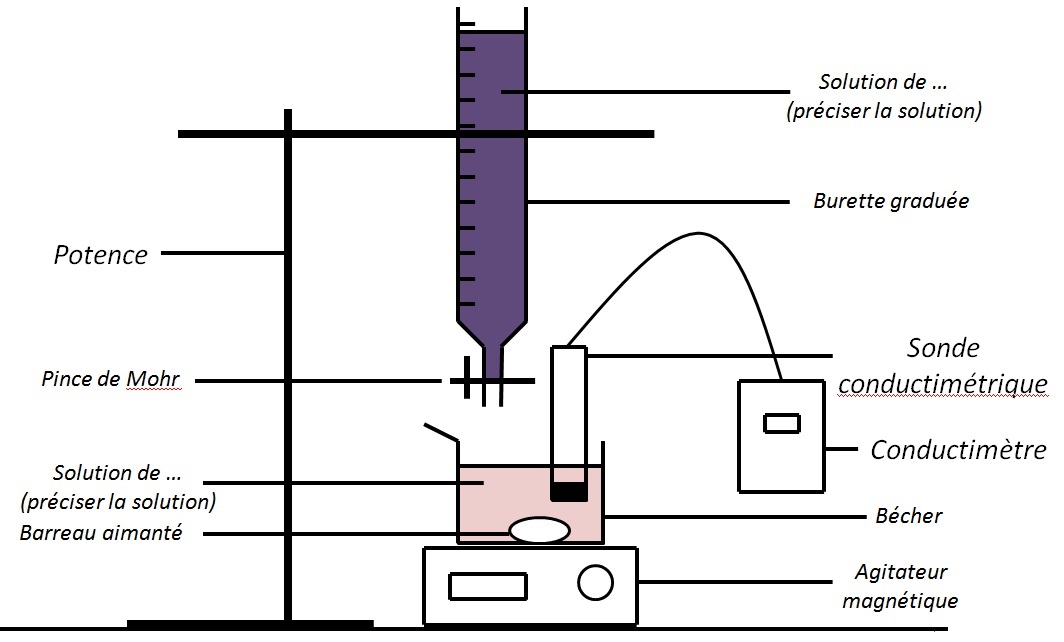
Pour suivre l’évolution de σ on remplira un tableau ressemblant fortement à celui utilisé pour le suivi pH-métrique :

Pour avoir de la conductivité il faut des ions, donc il y aura forcément des ions dans la réaction de dosage.
En effet, on rappelle la formule de la conductivité d’une solution :

σ est en S.m^-1 (S = Siemens)
λ_i est la conductivité molaire ionique des ions en S.m².mol^-1
[X_i] est la concentration molaire des ions en mol.m^-3

—
ATTENTION !! La concentration est en mol.m^-3 et non en mol.L^-1 comme c’est souvent le cas.
De plus, dans la formule seuls les ions interviennent, pas les autres espèces.
Mais ce sont TOUS les ions qui sont présents dans la formule, y compris les ions spectateurs (que les élèves oublient souvent…)
—

Après avoir rempli le tableau, on pourra placer les points sur un graphe puis tracer, ce qui nous donnera le style de graphe suivant :

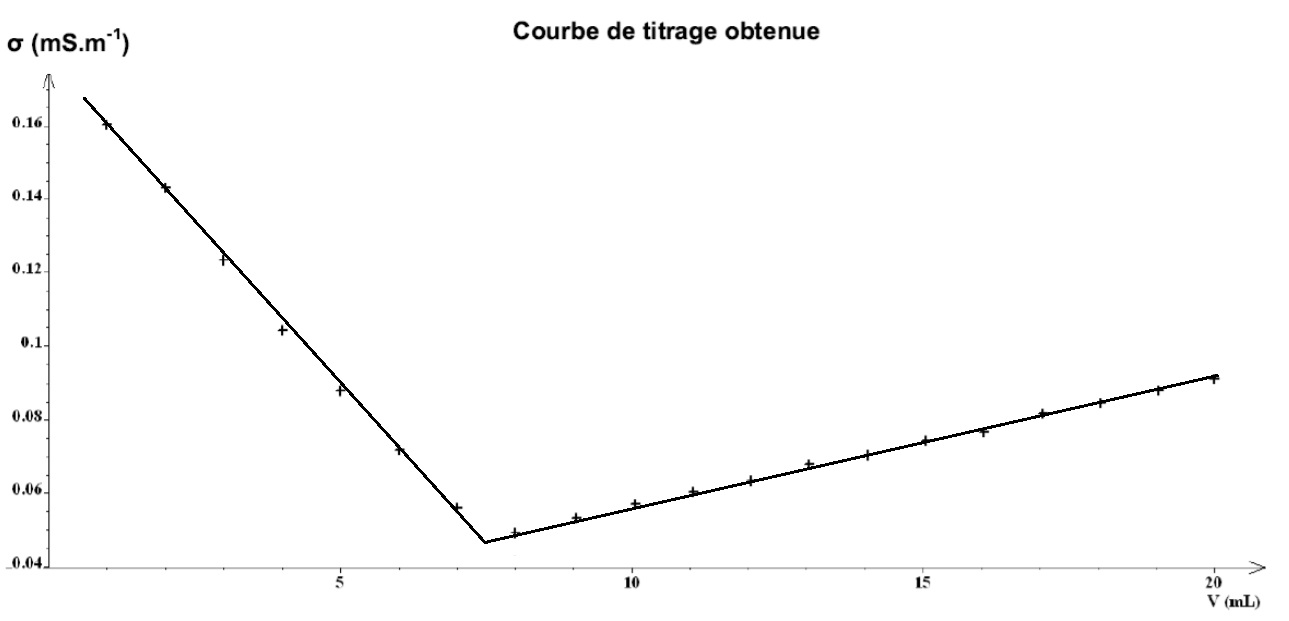
L’équivalence est repérée par le changement brutal de la courbe, ce qui est plutôt simple !

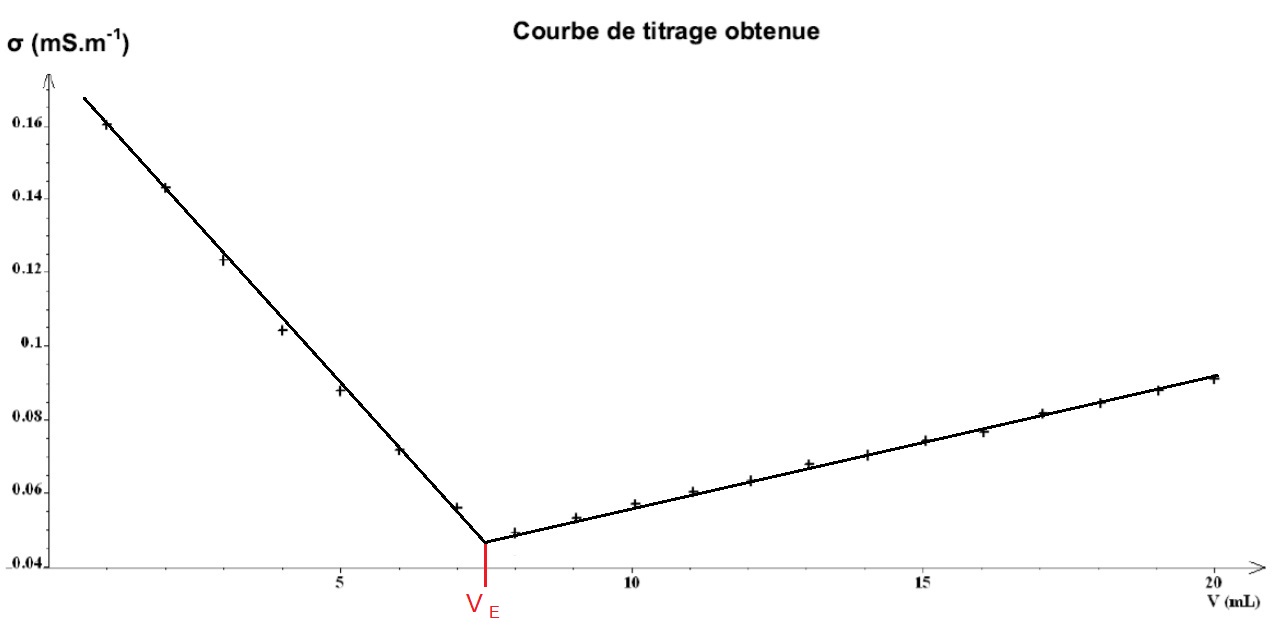
Ce graphe a été donné au Bac Liban en 2016. Voyons pourquoi on a obtenu une telle courbe.
Il s’agissait du dosage des ions chlorure contenus dans une solution de chlorure de sodium (Na⁺ + Cl^–) par une solution titrante de nitrate d‘argent (Ag⁺ + NO₃^–) et de concentration C (que l’on connaît).
L’énoncé précisait les conductivités molaires ioniques :

L’équation de la réaction était également donnée :
Ag⁺ + Cl^– → AgCl_(s)

Au début du dosage, il n’y a que la solution titrée dans le bécher, donc les ions Na⁺ et Cl^–.
La conductivité a alors pour expression :

Les ions Na⁺ étant spectateurs, leur concentration restera identique, et λ est une constante, donc λ_Na⁺[Na⁺] est une constante qui sera notée K.
On a donc initialement :

—
Remarque : en réalité, comme on va verser de la solution titrante, le volume de la solution va changer et donc la concentration de Na⁺ va aussi changer. Mais on suppose que le volume ajouté est négligeable devant le volume total donc on considère le volume de la solution comme constant. Dans la suite tous les volumes seront donc notés V_T, comme Volume Total, avec V_T constant.
Le volume versé sera lui simplement noté V (qui lui varie !).
—

On commence ensuite à verser du Ag⁺ + NO₃^– : les ions Ag⁺ réagissent et donc disparaissent : ils n’interviennent pas dans σ.
En revanche, des ions Cl^– réagissent également, leur quantité de matière diminue donc leur concentration aussi.
Mais il ne faut pas non plus oublier les ions NO₃^– ! Ils sont certes spectateurs mais sont présents dans la solution puisqu’on en verse mais qu’ils ne réagissent pas : ils vont donc apparaître dans σ.
En revanche, le produit de la réaction AgCl n’étant pas un ion, il n’intervient pas dans σ.
La conductivité a désormais pour valeur :

Le problème ici est que [Cl^–] diminue mais [ NO₃^–] augmente : comment savoir alors si σ va augmenter ou diminuer ??

C’est la qu’il est important de faire un tableau d’avancement !!
On note n₁ la quantité de matière initiale de Cl^–, et n_V la quantité de matière de solution titrante versée, on a alors :

Avant l’équivalence, on a :

et

En effet, la quantité de NO₃^– correspond à celle versée dans la solution puisque cet ion ne réagit pas.
De plus, d’après le tableau n_V – x = 0 donc n_V = x.
Mais on sait aussi que n_V = C x V, où C est la concentration de la solution titrante (connue) et V le volume versé.
Ainsi n_V = x = C x V

—
Attention ici à ne pas confondre V (le volume versé qui varie) avec V_T le volume totale de la solution qui est quasi-constant (considéré comme constant comme dit dans la remarque précédemment).
—

Remplaçons dans σ :

On factorise ensuite, et comme λ_Cl^–, n₁ et V_T sont constants, on regroupe le 1er terme avec la constante, ce qui donne une nouvelle constant K’, et on a alors :

On remarque alors que l’on vient de trouver l’équation d’une droite affine de style σ = aV + b.
Le fait qu’elle soit croissante ou décroissante dépendra du coefficient directeur a.
Ici on a :

C et V étant positifs, tout va dépendre des λ : ici λ_Cl^– > λ_NO3^– (d’après le tableau donné plus haut), donc a < 0 : la courbe sera une droite décroissante ! Et en effet on voit sur le graphique que la droite est bien décroissante avant l'équivalence. On peut même vérifier que le coefficient directeur a trouvée théoriquement avec le calcul ci-dessus correspond bien au coefficient directeur que l'on peut trouver graphiquement, comme en maths ! Et on peut faire de même pour l'ordonnée à l'origine. Ici nous n'allons pas le faire mais cela peut faire l'objet d'un exercice...

Voyons voir désormais ce qui se passe après l’équivalence.
Les ions Cl^– ont été entièrement consommés : ils n’apparaissent plus dans σ.
Les ions Na⁺ sont toujours en quantité constante.
Les ions NO₃^– sont toujours présents et leur quantité augmente puisqu’on continue de verser de la solution titrante.
Les ions Ag⁺ sont aussi présents et leur quantité augmente puisqu’on continue de verser de la solution titrante et qu’il n’y a plus d’ions Cl^– pour les faire réagir.

Ainsi la quantité d’ions ne fait qu’augmenter, donc la conductivité ne peut qu’augmenter : pas besoin de faire de calcul !
On peut quand même faire des calculs pour trouver l’expression du coefficient directeur comme précédemment (nous le ferons juste après).

Ce qu’il est important de comprendre c’est que, dans notre exemple, σ diminue avant l’équivalence mais augmente après l’équivalence : le point où le courbe change de sens correspond donc bien à l’équivalence.

—
De manière générale, σ ne peut qu’augmenter après l’équivalence car on rajoute de la solution titrante mais il n’y a pas de réaction : la quantité d’ions ne fait qu’augmenter (ou peut rester constante pour certains produits ou ions spectateurs).
—

Mais si σ augmentait avant l’équivalence, verrait-on quand même le changement au niveau de l’équivalence ??
Oui car on obtiendrait une courbe de ce type là :

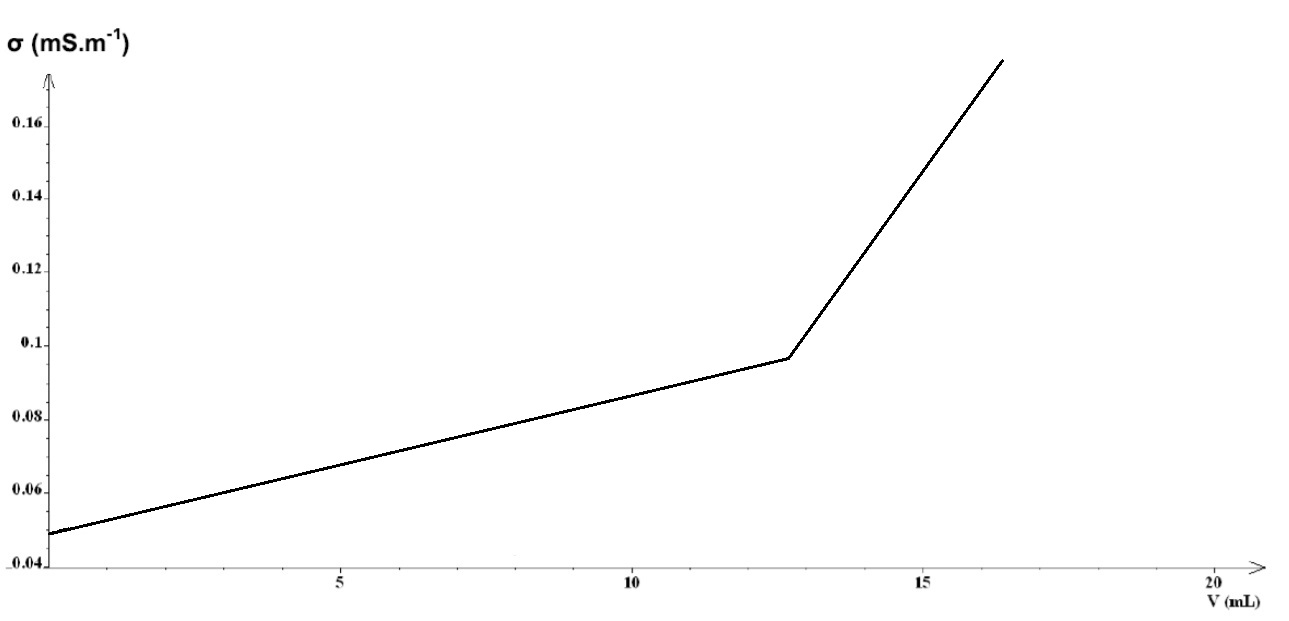
On obtient ainsi deux portions de droite différentes avant et après l’équivalence : cela signifie que le coefficient directeur doit être différent : vérifions par le calcul en calculant le coefficient directeur de la courbe après l’équivalence sur l’équation précédente. Après l’équivalence, il y a des ions Ag⁺, NO₃^– et Na⁺ : la quantité de Na⁺ étant constante on notera K le terme correspondant dans σ on a donc :

On a n_NO3^– = n_V = CV
n_Ag⁺ = n_V – x_E = CV- x_E

En regroupant comme précédemment, avec x_E constant que l’on met dans la constante, on obtient :

On voit que le coefficient directeur est :

qui est toujours positif puisque cette fois-ci on additionne les λ !
En revanche avant l’équivalence on avait :

On voit que l’on obtient deux expressions différentes donc le coefficient directeur sera nécessairement différent avant et après l’équivalence : on aura donc bien deux portions de droite différentes, toujours croissante après l’équivalence, mais croissante ou décroissante avant l’équivalence.

Propriétés de la réaction de dosage

Haut de page

On a vu qu’un dosage fait intervenir une équation chimique.
Cette équation, appelée équation de dosage, doit posséder 3 caractéristiques (sans quoi elle ne peut pas être une équation de dosage).
Elle doit être :

TOTALE
RAPIDE
UNIQUE

Elle doit être totale car à l’équivalence les deux réactifs doivent avoir disparu, elle ne peut donc pas être limitée.
Elle doit être rapide car quand on verse de la solution titrante il faut que la réaction se fasse instantanément car on doit relever la mesure (du pH ou de la conductivité) ou regarder la couleur avant de continuer à verser de la solution. Si on doit attendre 5 minutes avant de verser à nouveau de la solution titrante, le dosage risque de prendre beaucoup de temps…
Et elle doit être unique car si une autre réaction se déroule en même temps, les calculs effectués avec le tableau d’avancement seraient complètement faussés !

En contrôle et au Bac, il est très souvent demandé de donner une ou plusieurs caractéristiques d’une réaction de dosage, ce sont des points gagnés très facilement ! (si bien sûr tu as appris ce qui précède ).

Piège à éviter

Haut de page

Nous terminerons ce chapitre par un piège classique que tu dois avoir en tête afin de ne pas faire d’erreur lors des examens.
La concentration inconnue est parfois si élevée que le volume équivalent serait beaucoup trop important si on réalisait le dosage tel quel (par exemple on aurait V_E = 100 mL) : cela n’est pas envisageable car la burette graduée a une capacité limitée, et le dosage serait beaucoup trop long (car il faudrait relever la valeur du pH de trop nombreuses fois par exemple).
L’idée est donc de diluer la solution titrée afin de diminuer le volume équivalent : si on dilue d’un facteur 10, la concentration inconnue sera divisée par 10 et le volume équivalent également !
Ainsi un volume équivalent de 120 mL passerait à 12 mL si on dilue la solution d’un facteur 10 par exemple.

Il faut donc déjà faire une dilution (voir la page sur la dilution).
Mais il ne faut surtout pas oublier de multiplier la concentration à la fin !!!
En effet, la concentration que l’on trouvera grâce au dosage sera celle de la solution diluée, pas de la solution initiale !
Ainsi, si par exemple on a dilué d’un facteur 8 la solution initiale, il faudrait multiplier par 8 la concentration trouvée avec le dosage pour avoir la concentration de la solution initiale.

Nous verrons un exemple dans les exercices, disponibles juste en-dessous !

Exercices

Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !

Sommaire des coursHaut de la page