La dissolution

Sommaire

Introduction
Solvant, soluté et solution
Protocole expérimental

Introduction

Nous allons voir dans ce chapitre quelque chose que tu feras parfois en TP de chimie : la dissolution, à ne pas confondre avec la dilution qui fait l’objet d’un chapitre spécifique sur la dilution.
Nous verrons les calculs ainsi que le protocole expérimental de la dissolution qui pourra t’être demandé en TP mais aussi en contrôle ou au bac.

Petite remarque : nous parlerons d’erlenmeyer dans le protocole, c’est la même chose qu’une fiole

Solvant, soluté et solution

La dissolution consiste à dissoudre une espèce dans un liquide. Nous ne verrons que la dissolution d’un solide dans un liquide car on ne fait que celle-là au lycée.
Tu fais déjà sans le savoir des dissolutions à la maison : par exemple quand tu rajoutes du lait avec du chocolat en poudre : le chocolat est dissous dans le lait. De même quand tu rajoutes de l’eau dans du café en poudre.

Il y a donc 3 choses différentes : le solide, le liquide et le mélange des deux lui aussi liquide.
Le solide est appelé soluté.
Le liquide est appelé solvant.
Le mélange des deux est appelé solution.

Le mélange d’un soluté et d’un solvant donne donc une solution.
Voyons les calculs que l’on peut te demander.

Le soluté étant solide il a une masse notée m, et on note M la masse molaire de ce solide (on peut donc calculer la quantité de matière n).
Le solvant est liquide et a donc un volume noté V.
La solution a le même volume V, et une concentration noté C.

Remarque : le solvant et la solution ont le même volume car on considère que l’ajout de soluté ne fera que très peu varier le volume.

Prenons un exemple : on a du chlorure de sodium solide (NaCl, le soluté) que l’on dissous dans de l’eau (le solvant).
On donne M(NaCl) = 58,4 g.mol^-1.
Imaginons que l’on souhaite 200 mL de solution dont la concentration en sodium ([Na⁺]) soit de 2,00 × 10^-1 mol.L^-1.
Quelle masse de NaCl doit-on dissoudre ?

Écrivons tout d’abord l’équation de dissolution :

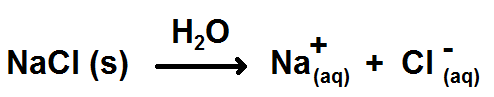
Comme tu le vois c’est une équation un peu particulière car l’eau n’apparaît ni dans les produits ni dans les réactifs mais au-dessus de la flèche. En effet, l’eau ne se transforme pas, mais elle permet au solide de se transformer en ions.
D’ailleurs, le (s) indique que NaCl est solide, tandis que le (aq) indique que les deux ions sont en solution aqueuse (normal puisque le solvant est l’eau).

Comme les coefficients stœchiométriques sont 1 pour les deux ions, cela montre que :
[Na⁺] = n/V et [Cl^–] = n/V (on verra après un exemple où ce n’est pas le cas).

Le n correspond comme dit plus haut à la quantité de matière du NaCl. On peut calculer la masse correspondante :
m = n × M.
Or on a vu que n = [Na⁺] × V, on a donc :
m = [Na⁺] × V × M

Il suffit de remplacer (en pensant à convertir le volume) :
m = 2,00 × 10^-1 × 200 × 10^-3 × 58,4
m = 2,34 g

Il faudra donc dissoudre 2,34 g de NaCl solide dans 200 mL d’eau.

Comme tu le vois on a simplement appliqué les formules que l’on connaît, à savoir m = n × M et n = C × V.

Prenons un autre exemple : on a du sulfate d’aluminium Al₂(SO₄)₃(s) de masse molaire
342 g.mol^-1 que l’on dissout dans 400 mL d’eau.
On souhaite une concentration en ions Al³⁺ de 5,00 × 10^-1 mol.L^-1.
Quelle masse doit-on dissoudre ?
Écrivons d’abord l’équation de dissolution :

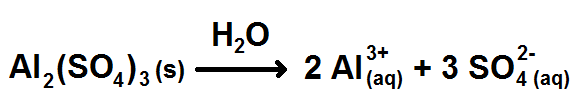
Faisons le tableau d’avancement de cette réaction :

	Al2(SO4)3(s)	→	2 Al3+	+	3 SO42-
Etat Initial	n		0		0
Etat Final	n – xmax = 0		2xmax		3xmax

La dissolution étant totale, n – x_max = 0, donc x_max = n
On a donc : n_Al³⁺ = 2x_max = 2n et n_SO4^2- = 3x_max = 3n

Dans l’énoncé il est dit que l’on veut [Al³⁺] = 5,00 × 10^-1 mol.L^-1.
On a n_Al³⁺ = 2n et n_Al³⁺ = [Al³⁺] × V.
D’où : [Al³⁺] × V = 2n

Or m = n × M, d’où :

Il faudra donc dissoudre 34,2 g de sulfate d’aluminium dans 400 mL d’eau.

Comme tu le vois l’exemple était ici un peu plus compliqué car les coefficients stœchiométriques de l’équation n’étaient pas 1. Il faut donc faire le tableau d’avancement de l’équation et trouver les relations.

Voyons maintenant le protocole expérimental pour réaliser de telles dissolutions.

Protocole expérimental

Haut de page

Les grandes étapes du protocole expérimental sont les suivantes :
– peser la masse de soluté
– la verser dans un récipient approprié
– verser le solvant

Nous allons détailler chacune de ces étapes :

1ère étape : peser la masse de soluté.
Il faut d’abord calculer la masse de soluté que l’on va dissoudre. Nous avons vu juste avant comment calculer cette masse.
On va supposer ici qu’il en faut 5,00 g.

Nous allons donc prendre une balance avec une coupelle vide que l’on met sur la balance.

—
Ne pas oublier de tarer la balance une fois que la coupelle a été mise sur la balance !
Tarer permet de remettre à zéro la balance, comme ça la masse de la coupelle n’est pas prise en compte.
—

On peut alors peser la masse de soluté que l’on souhaite en la mettant sur la coupelle :

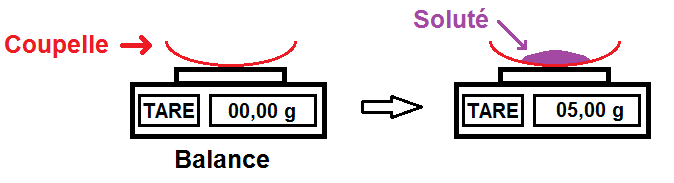
2ème étape : verser le soluté dans un récipient approprié
Une fois pesé, il faut verser le soluté dans un récipient, mais pas n’importe lequel !
Le volume de la solution que l’on souhaite est presque toujours donné dans l’énoncé. Ce volume devant être précis, il faut prendre un erlenmeyer jaugé (tous les volumes précis doivent être faits avec de la verrerie jaugée).
Si on veut 50 mL de solution, on prendra un erlenmeyer jaugé de 50 mL.

Cependant il faut faire attention à ne pas perdre une miette de soluté lors du transvasement !
On prend alors un entonnoir que l’on met dans le col de l’erlenmeyer, et on verse le contenu de la coupelle dans l’entonnoir :

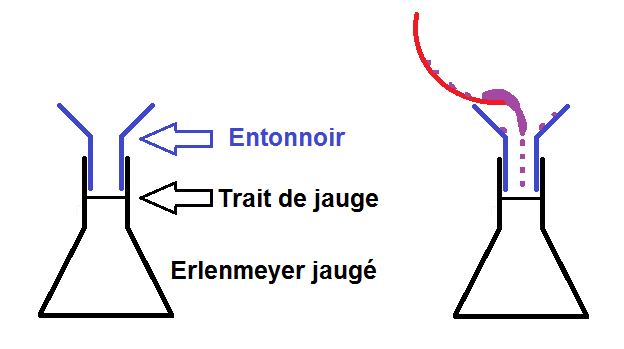
L’entonnoir permet de ne pas verser de soluté à côté, mais il ne permet pas d’avoir TOUT le soluté !
En effet, il peut rester du soluté accroché dans la coupelle et sur l’entonnoir.
La solution : rincer la coupelle et l’entonnoir avec une pissette d’eau distillée afin de récupérer tout le soluté resté accroché :

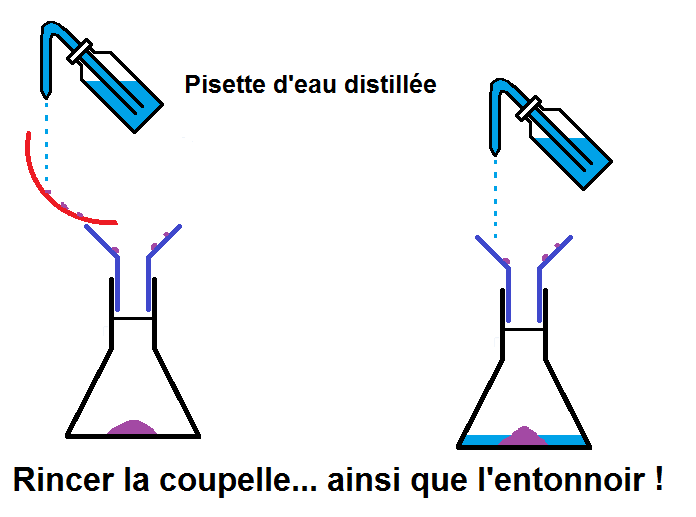
On a maintenant tout le soluté dans l’erlenmeyer avec un peu d’eau distillée (celle utilisée pour rincer la coupelle et l’entonnoir).

3ème étape : verser le solvant
Il faut maintenant compléter l’erlenmeyer jusqu’au trait de jauge avec le solvant, c’est-à-dire l’eau distillée.
Mais cela ne va pas se faire en une seule fois !!
En effet, on va d’abord remplir l’erlenmeyer jusqu’à environ 2/3, puis on va agiter pour que le soluté se dissolve bien dans l’eau.
Une fois que le soluté est bien dissous, on complète jusqu’au trait de jauge avant de remuer une fois de plus pour bien homogénéiser :

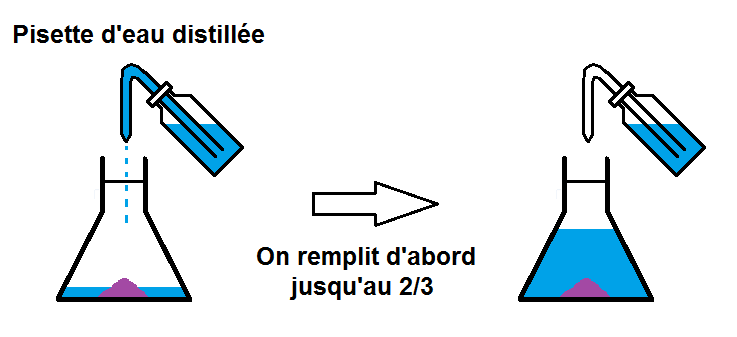
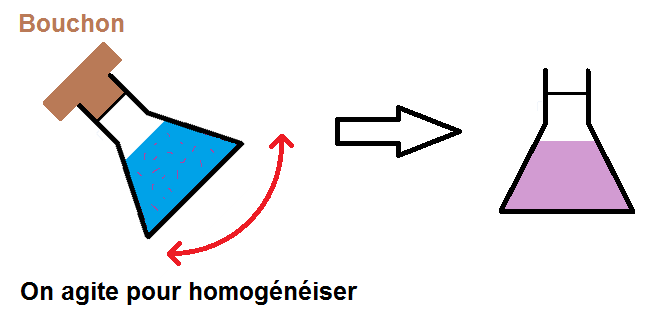
(on suppose ici que la solution est colorée mais elle pourrait être incolore)

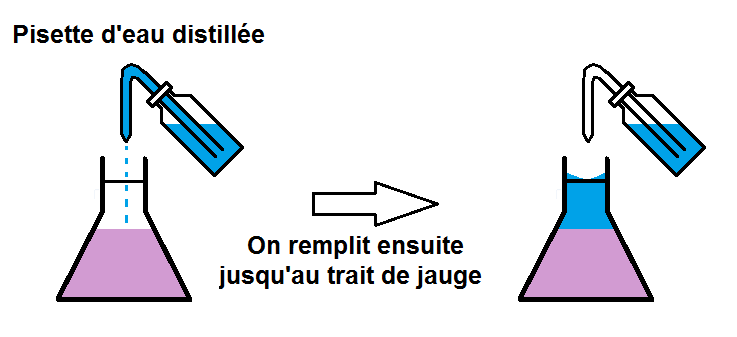
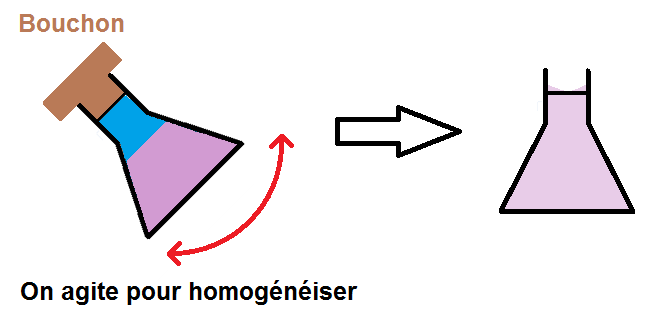
Et voilà on a obtenu notre solution !

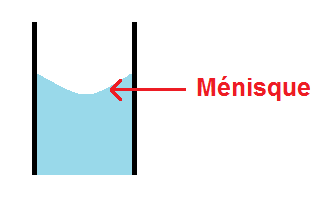
Attention cependant au ménisque et au défaut de parallaxe au niveau du trait de jauge !
En effet, au niveau du trait de jauge la solution ne sera pas plate mais légèrement arrondie : c’est un ménisque.

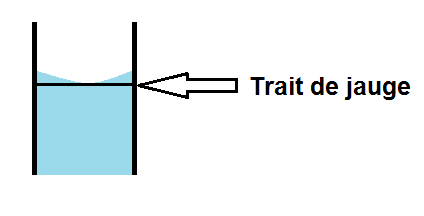
La règle est la suivante : le bas du ménisque doit être au niveau du trait de jauge :

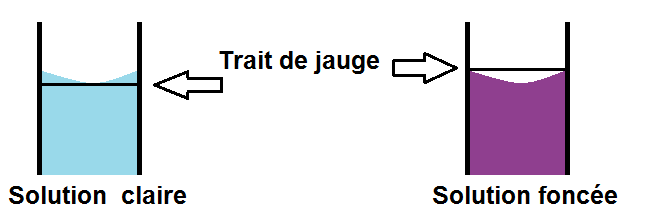
Il existe cependant une exception : pour les solutions foncées.
En effet, si la solution est trop foncée, tu ne pourras pas voir le trait de jauge. Pour les solutions foncées, on prend donc le trait de jauge en haut du ménisque :

Il faut faire également attention au défaut de parallaxe, c’est-à-dire qu’il faut mettre l’œil en face du trait de jauge :

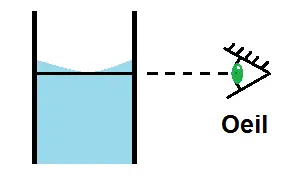
Pour éviter le défaut de parallaxe, l’œil doit être en face du trait de jauge

Nous avons récapitulé les principales étapes pour que tu aies une idée plus générale du protocole :

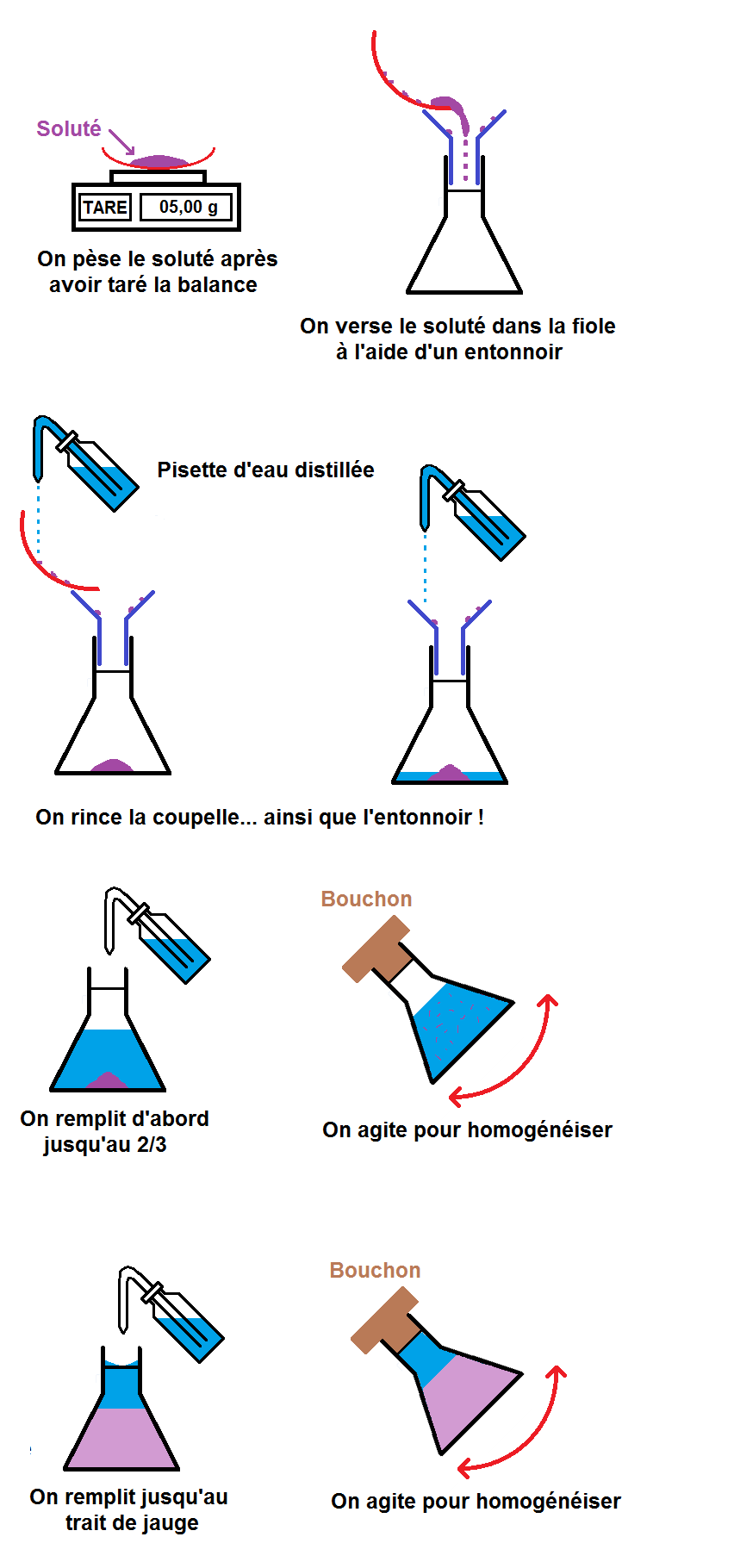
Maintenant tu connais tout sur la dissolution !

Sommaire des coursHaut de la page