Sommaire
Introduction
Second Principe de la thermodynamique : introduction de l’entropie
Calcul de la variation d’entropie
Cas particulier : adiabatique réversible
Entropie de changement d’état
Identité thermodynamique
Exercices
Nous allons parler dans ce chapitre du second principe de la thermodynamique. Il faut tout d’abord que tu aies impérativement lu le chapitre sur le premier principe sinon tu risques de ne pas comprendre grand chose !
Le second principe est complémentaire du premier principe. Il s’utilise souvent dans l’étude des machines thermiques, qui fera l’objet d’un chapitre séparé, ce pourquoi l’étude du second principe est un prérequis essentiel à l’étude des machines thermiques.
Petit point littéraire avant de commencer : dit-on second ou deuxième principe ?? 
La règle est simple : on dit deuxième s’il y a au moins un troisième, sinon on dit second. Comme il n’y a que 2 principes de la thermodynamique, il faut dire « second » principe et non 2ème, mais tu verras que cette règle n’est pas forcément respectée, et on ne t’en tiendra pas rigueur dans tes copies (sauf si le correcteur est tatillon !  )
)
Le premier principe permet de connaître les variations des fonctions d’état lors d’une transformation mais ne permet pas de prévoir le sens de cette transformation.
En effet, supposons que l’on mélange de l’eau chaude avec de l’eau froide : on aura au final de l’eau tiède. Il est impossible évidemment de séparer l’eau chaude et l’eau froide une fois que les deux se sont mélangées, mais le premier principe ne l’interdit pas !
On va donc introduire une nouvelle fonction d’état, appelée entropie, notée S, qui est en J.K-1.
L’entropie est une mesure du désordre : plus S est grand, plus cela signifie que le système est en désordre.
Exemple : si on a un tas de feuilles empilées parfaitement les unes sur les autres, puis que l’on renverse ce tas au sol, les feuilles vont s’éparpiller : l’entropie des feuilles au sol est plus grande que celle du tas car il y a plus de désordre.
Au cours d’une transformation, S étant une fonction d’état, on peut parler de ΔS : cette variation d’entropie peut se décomposer en 2 parties : l’entropie échangée avec le milieu extérieur, notée Séch, et l’entropie créée pendant la transformation, notée Scréée :
\(\displaystyle \Delta S = S_{ech} + S_{creee} \)
Remarque importante : tu auras sûrement remarqué que l’on a mis Δ devant S mais pas devant Séch et Scréée car ce ne sont pas des fonctions d’état, comme W et Q.
Par ailleurs, si on reprend l’exemple du tas de feuilles, une fois les feuilles au sol elles ne peuvent pas se remettre d’elle-même en tas : autrement dit, un système ne peut naturellement que créer du désordre, donc créer de l’entropie, on en déduit que :
\(\displaystyle S_{créée} \ge 0 \)
Il y a un cas particulier très important : Scréée = 0. En effet, cela signifie qu’il n’y a pas d’entropie créée, donc pas de désordre créé lors de la transformation, il est donc possible de faire la transformation inverse : la transformation est réversible !
Ainsi :
\(\displaystyle S_{créée} = 0 \Leftrightarrow la \, transformation \)
\(\displaystyle est \, réversible \)
Cela signifie que pour une transformation irréversible, Scréée > 0.
Ces 3 premières formules constituent ce que l’on appelle le second principe de la thermodynamique : contrairement au premier principe qui s’exprime avec une seule équation, le second principe est un peu plus complet.
Quant à l’entropie échangée Séch, elle se calcule de la manière suivante :
\(\displaystyle S_{ech} = \int \frac{dQ}{T} \)
Il est fréquent de noter Qrév le Q correspondant à une transformation réversible, Qirrév le Q correspondant à une transformation irréversible,
Pour une transformation réversible, Scréée = 0, d’où :
\(\textstyle \Delta S = \int \frac{dQ_{rev}}{T} \)
Pour une transformation irréversible :
\(\textstyle \Delta S = \int \frac{dQ_{irrév}}{T} + S_{créée} \)
Comme Scréée > 0 (car irréversible), on en déduit que :
\(\displaystyle \Delta S \ge \int \frac{dQ_{irrév}}{T} \)
Il s’agit d’une autre manière d’exprimer le second principe.
Voyons maintenant le calcul de Séch pour 3 transformations souvent rencontrées, les isothermes, isobares et isochores.
Remarque : de nombreuses formules utilisées dans les démonstrations qui suivent font intervenir des relations vues dans le chapitre sur le premier principe, on les admettra sans les redémontrer.
Pour une transformation isobare :
On sait que dQ = dH, donc dQ = CPdT, d’où :
\(\textstyle S_{ech} = \int \frac{dQ}{T} \)
\(\textstyle S_{ech} = \int \frac{C_P dT}{T} \)
\(\textstyle S_{ech} = C_P \int \frac{dT}{T} \)
\(\textstyle S_{ech} = C_P ln(\frac{T_2}{T_1}) \)
Pour une transformation isochore :
On sait que dQ = dU, donc dQ = CVdT, d’où :
\(\textstyle S_{ech} = \int \frac{dQ}{T} \)
\(\textstyle S_{ech} = \int \frac{C_V dT}{T} \)
\(\textstyle S_{ech} = C_P \int \frac{dT}{T} \)
\(\textstyle S_{ech} = C_V ln(\frac{T_2}{T_1}) \)
Remarque : on retrouve la même expression que pour une isobare mais avec CV à la place de CP.
Pour une transformation isotherme :
On sait que dU = 0, donc d’après le 1er principe dQ = – dW.
Or dW = -PdV, donc dQ = PdV, d’où :
\(\textstyle S_{ech} = \int \frac{dQ}{T} \)
\(\textstyle S_{ech} = \int \frac{PdV}{T} \)
En considérant un gaz parfait :
\(\textstyle \frac{P}{T} =\frac{nR}{V} \)
D’où :
\(\textstyle S_{ech} = \int \frac{nRdV}{V} \)
\(\textstyle S_{ech} = nR \int \frac{dV}{V} \)
\(\textstyle S_{ech} = nR ln(\frac{V_2}{V_1}) \)
Comme tu le vois, rien de compliqué !
Ces formules ne sont pas vraiment à connaître mais il faut savoir les redémontrer 
Voyons maintenant un autre cas particulier très courant.
En exercice, on rencontrera souvent des transformations adiabatiques réversibles.
Adiabatique signifie Q = 0, donc Séch = 0
Réversible signifie Scréée = 0
On en déduit donc que
\(\displaystyle \Delta S = 0 \, pour \, une \)
\(\displaystyle adiabatique \, réversible \)
Cela signifie que l’entropie du système ne varie pas : on dit qu’elle est isentropique.
—
Une transformation adiabatique réversible est isentropique
—
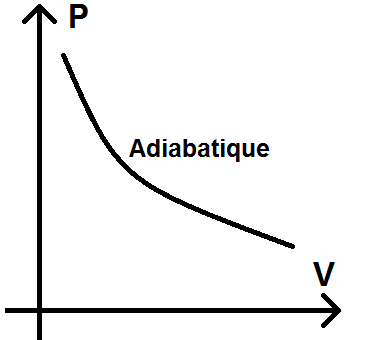
De plus, pour les transformations adiabatiques, on peut utiliser les formules de Laplace, notamment PVγ = constant.
D’où P = constante/Vγ : on en déduit que dans le diagramme de Clapeyron, une adiabatique réversible est une hyperbole décroissante (un peu comme la fonction inverse) :
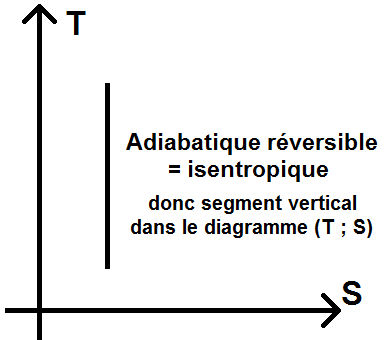
Il existe aussi des diagrammes (T ; S), appelés diagrammes entropiques.
Une adiabatique réversible étant isentropique d’après ce qui précède, elle sera représentée par un segment vertical :
Lors d’un changement d’état, on avait vu que la pression est constante, donc ΔH = Q.
De plus, lors d’un changement d’état, la température est constante, donc :
\(\textstyle S_{ech} = \int \frac{dQ}{T} \)
\(\textstyle S_{ech} = \frac{1}{T} \int dQ \)
\(\textstyle S_{ech} = \frac{Q}{T} \)
\(\textstyle S_{ech} = \frac{\Delta H}{T} \)
De plus Scréée = 0 car un changement d’état est réversible, donc Δ S = Séch, on en déduit que :
\(\displaystyle \Delta S = \frac{\Delta H}{T} \)
pour un changement d’état
C’est ce que l’on appelle l’entropie de changement d’état à la température T.
Elle dépend directement de l’enthalpie de changement d’état à la température T dont on avait parlé dans le cours sur le premier principe (qui correspond à la chaleur latente).
Ainsi, par exemple, à une température T donnée :
\(\textstyle \Delta S_{fusion} = \frac{\Delta H_{fusion}}{T} \)
Voyons maintenant une formule qui sera souvent utilisée en exercice : l’identité thermodynamique.
Considérons une transformation réversible. D’après ce qui précède, Scréée = 0, donc :
\(\textstyle dS = dS_{ech} = \frac{dQ_{rev}}{T} \)
D’où :
\(\textstyle dQ_{rev} = TdS \)
D’après le 1er principe : dU = dQ + dW, avec dQ = dQrév, et dW = -PdV, donc :
\(\textstyle dU = dQ_{rev} – PdV \)
\(\displaystyle dU = TdS – PdV \)
Cette égalité est ce que l’on appelle l’identité thermodynamique.
Cette égalité a été démontrée dans le cas d’une transformation réversible, mais on pourrait montrer qu’elle est également vraie dans le cas d’une transformation irréversible.
L’identité thermodynamique est donc vraie pour toute transformation.
Voyons un exemple d’application très simple : on cherche la variation d’entropie entre deux états (notés 1 et 2) pour une transformation isochore.
D’après l’identité thermodynamique : dU = TdS – PdV.
Or la transformation est isochore, donc dV = 0, d’où dU = TdS.
On sait que dU = CvdT (car isochore), d’où : CvdT = TdS
Il n’y a plus qu’à regroupe les variables et intégrer (on considère Cv constant) :
\(\textstyle C_v \frac{dT}{T} = dS \)
\(\textstyle C_v \int\limits_{T_1}^{T_2} \frac{dT}{T} = \int\limits_1^2 dS \)
\(\textstyle C_v ln(\frac{T_2}{T_1}) = \Delta S \)
On retrouve la formule trouvée précédemment !
Ce chapitre sur le second principe est désormais terminé, tu peux maintenant regarder le cours sur les machines thermiques qui est une des principales applications du second principe de la thermodynamique.
Les exercices sur ce chapitre seront bientôt disponibles !
Sommaire des coursHaut de la page



C’est très utile ce chapitre et compréhensif
Merci, c’est bien expliqué.
super cours merci !