Sommaire
Introduction
Force d’attraction gravitationnelle
Le poids
Accélération de la pesanteur
Force électrostatique
Exercices
Dans ce chapitre nous allons voir une notion très importante en physique que l’on utilise dans la vie courante : le poids. Mais on va voir que dans la vie courante on dit n’importe quoi…
Avant de passer au poids proprement dit nous allons voir ce qui se passe dans l’espace (ça rime !!!…  ).
).
Nous verrons enfin une force similaire mais pour les charges électriques (avec quelques subtilités^^).
A noter que certains vecteurs seront notés sans la flèche mais en gras dans ce chapitre (pour t’habituer à cette notation que l’on retrouve parfois dans les exercices  )
)
La force d’attraction universelle existe dès qu’il y a deux objets qui ont une masse.
Mais alors, cette force existe tout le temps diras-tu ??  Par exemple entre ta main et ton bureau ? Oui en effet mais elle est tellement faible qu’elle est négligeable… (on fera le calcul tout à l’heure).
Par exemple entre ta main et ton bureau ? Oui en effet mais elle est tellement faible qu’elle est négligeable… (on fera le calcul tout à l’heure).
En fait on va surtout calculer cette force entre deux ENOOOOOORMES objets, à savoir… des planètes !
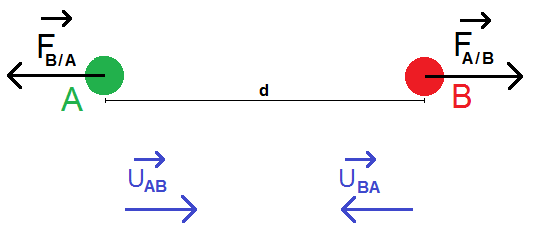
On va noter A et B deux planètes, de masse mA et mB. Ces deux planètes sont séparées d’une distance notée d.
On a alors le schéma suivant :
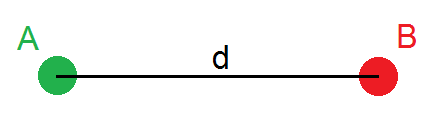
La formule de la norme de la force d’attraction gravitationnelle est la suivante :
\(\displaystyle F = G \times \frac{m_A \times m_B}{d^2} \)
—
ATTENTION aux unités !!! Dans cette formule on aura TOUJOURS F en Newton (N), m en kilogrammes (kg) et d en mètres (m).
Il faut faire très attention que souvent, d en donné en kilomètres (vu que c’est la distance entre deux planètes donc très grande), il faut donc systématiquement la convertir en mètres.
Et G est en… on va voir ça tout de suite 
—
Mais qu’est-ce-que c’est que ce G tout d’abord ?
C’est une constante que l’on appelle constante de gravitation universelle.
Cette constante a pour valeur G = 6,67 x 10-11 N.m2.kg-2
Mais cette valeur est approchée à 2 chiffres après la virgule, dans l’énoncé ils peuvent donner plus ou moins de chiffres significatifs.
Cependant tu n’as pas à retenir cette valeur, elle sera toujours donnée dans l’énoncé (par contre tu peux retenir l’ordre de grandeur).
A noter que cette constante possède plusieurs noms : constante gravitationnelle, constante universelle de gravitation etc… mais la plus courante est constante de gravitation universelle, elle sera toujours notée G.
Parfois dans l’énoncé il y a marqué G = 6,67 x 10-11 S.I. : le S.I. signifie système international, ne t’en occupe pas et fais comme si il était marqué N.m2.kg-2.
Ils peuvent cependant te demander l’unité de G. Pour cela rien de plus simple : d’après la formule ci-dessus, on a :
\(\textstyle G = \frac{F \times d^2}{m_A \times m_B} \)
Or F est en N, d en m et mA et mB en kg.
Donc G est en N.m2.kg-2 
Voyons maintenant le vecteur force : en effet, on vient de voir la norme de la force, mais on rappelle qu’une force est représentée par un vecteur, avec un point d’application, une direction, un sens et une norme.
Pour la norme, c’est fait. Pour la direction c’est simple : c’est la droite reliant les centres des deux planètes.
Et pour le sens ?? Tout dépend !
En fait les deux planètes vont s’attirer mutuellement l’une vers l’autre, d’où le nom de force d’attraction.
La planète A va attirer B vers A, et la planète B va attirer A vers B.
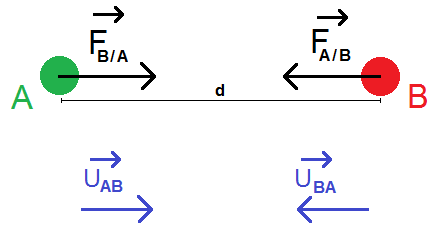
On a donc deux forces : FA/B et FB/A (en gras car ce sont des vecteurs).
FA/B est la force que A exerce sur B : le point d’application est le centre de B (car la force s’exerce sur B), et elle est dirigée vers A (puisque la force que A exerce sur B attire B vers A).
C’est évidemment l’inverse pour FA/B, ce qui nous donne le schéma suivant :

Ce schéma est à retenir par cœur car on te demande très souvent de le refaire.
Concernant le vecteur, il va falloir en créer un afin d’avoir une formule pour le vecteur force.
Pour cela, on note uAB le vecteur UNITAIRE de A vers B (c’est facile à retenir : uAB A vers B).
Et bien sûr uBA est le vecteur UNITAIRE de B vers A.
Qu’est-ce-qu’on remarque alors ? Que FA/B est de B vers A, donc on pourrait le mettre selon uBA. Mais pour garder une certaine logique, on va le mettre selon uAB mais avec un signe « moins » : ce signe montre que c’est une force « d’attraction ».
On a donc :
\(\displaystyle \overrightarrow{F_{A/B}} = -G \times \frac{m_A \times m_B}{d^2} \overrightarrow{u_{AB}} \)
Comme tu le vois c’est facile à retenir car on a FA/B et uAB, c’est facile à retenir 
—
ATTENTION à ne pas oublier le signe – dans la formule !!!
—
De même on a évidemment :
\(\displaystyle \overrightarrow{F_{B/A}} = -G \times \frac{m_A \times m_B}{d^2} \overrightarrow{u_{BA}} \)
L’intérêt de cette technique (de garder le même ordre des lettres dans le vecteur force et dans le vecteur unitaire) est que si on change les lettres, par exemple les planètes ne s’appellent plus A et B mais S et T, tu n’as qu’à remplacer A et B par S et T sans te préoccuper de l’ordre : il faut juste conserver le même ordre dans la force et le vecteur.
Par exemple :
\(\textstyle \overrightarrow{F_{S/T}} = -G \times \frac{m_S \times m_T}{d^2} \overrightarrow{u_{ST}} \)
\(\textstyle \overrightarrow{F_{T/S}} = -G \times \frac{m_S \times m_T}{d^2} \overrightarrow{u_{TS}} \)
Faisons un petit schéma pour récapituler :
—
ATTENTION !! Les deux vecteurs force doivent avoir la même longueur car ils ont la même norme !
En effet, dans la formule pour la force, G et d sont les mêmes que l’on calcule FA/B ou FB/A. La seule chose qu’il faudrait changer serait de remplacer mA × mB par mB × mA, ce qui ne changerait absolument rien !!!
Donc la norme de FA/B est la même que celle de FB/A
On peut donc mettre les masses dans l’ordre que l’on veut dans la formule.
—
Ayant noté tout cela, il est assez facile de voir que :
\(\displaystyle \overrightarrow{F_{A/B}} = -\overrightarrow{F_{B/A}} \)
et
\(\displaystyle \overrightarrow{u_{AB}} = -\overrightarrow{u_{BA}} \)
Voyons maintenant un petit point important : on a introduit uAB et uBA unitaires parce qu’il fallait des vecteurs.
Signalons au passage que ces vecteurs ont été choisis unitaires afin que cela ne change pas la norme de la force.
Sauf que dans l’énoncé ces vecteurs ne sont pas forcément donnés, et normalement il ne faut pas « créer » de nouvelles choses autres que celles données dans l’énoncé. Il y a alors un moyen simple de remédier à ce problème.
Pour remplacer le vecteur uAB par exemple, il faut un vecteur dont la direction soit la droite (AB), de sens A vers B, et unitaire. La réponse est toute trouvée : il s’agit du vecteur AB divisé par sa norme :
\(\displaystyle \overrightarrow{u_{AB}} = \frac{\overrightarrow{AB}}{||\overrightarrow{AB}||} \)
(on rappelle que la norme du vecteur AB se note entre deux barres de chaque côté)
On peut donc écrire les formules précédentes d’une autre manière :
\(\displaystyle \overrightarrow{F_{A/B}} = -G \times \frac{m_A \times m_B}{d^2} \frac{\overrightarrow{AB}}{||\overrightarrow{AB}||} \)
\(\displaystyle \overrightarrow{F_{B/A}} = -G \times \frac{m_A \times m_B}{d^2} \frac{\overrightarrow{BA}}{||\overrightarrow{BA}||} \)
Pour choisir quelle formule appliquer, tout dépend de l’énoncé. Il arrive même que l’énoncé te donne juste un vecteur u unitaire en précisant le sens et c’est à toi de t’adapter dans la formule !
Si tu as bien compris tout cela, et que tu as bien le schéma récapitulatif en tête, nous allons pouvoir passer au poids !
En fait le poids est un cas particulier de la force dont on vient de parler.
Il s’agit en effet de la force d’attraction entre deux objets, sauf que ces objets vont être la Terre, et un objet posé sur la Terre :
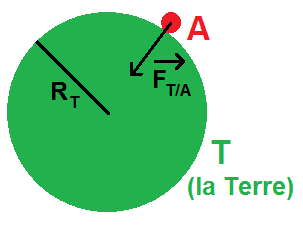
Ici évidemment le schéma n’est pas à l’échelle, l’objet A est minuscule par rapport à la Terre.
Ainsi on va noter A l’objet posé sur la Terre, de masse mA, et T la Terre, de masse mT.
Concernant la distance d de tout à l’heure, il est évident que d’après le schéma précédent il s’agit du rayon de la Terre !
Ce rayon sera noté RT, donc d = RT, qui est une constante, environ 6400 km (à convertir en mètres bien entendu  ).
).
Et le poids noté P correspond à la force exercée PAR LA TERRE sur l’objet situé A LA SURFACE de la Terre :
\(\displaystyle \overrightarrow{P} = \overrightarrow{F_{T/A}} = -G \frac{m_T \times m_A}{(R_T)^2} \overrightarrow{u} \)
en notant u le vecteur unitaire dirigé du centre de la Terre vers l’objet
Or G, mT et RT sont des constantes, que l’on peut regroupe :
\(\displaystyle \overrightarrow{P} = -m_A \frac{G \times m_T}{(R_T)^2} \overrightarrow{u} \)
et en notant
\(\displaystyle g = \frac{G \times m_T}{(R_T)^2} \)
on obtient
\(\displaystyle \overrightarrow{P} = -m_A \times g \overrightarrow{u} \)
Et voilà on vient de trouver l’expression du poids !
Et en bonus on vient de trouver l’expression de g  (on en reparle plus loin)
(on en reparle plus loin)
Retiens bien ce calcul car souvent on te demande de calculer g, et il faut d’abord faire cette petite démonstration avant de passer à l’application numérique (on reviendra sur g plus loin).
Comme tu le vois le poids n’est qu’un cas particulier de la force d’attraction gravitationnelle.
Par contre pour le schéma, vu que l’on travaille sur un objet qui est à la surface de la Terre, on utilise plus souvent ce schéma là :
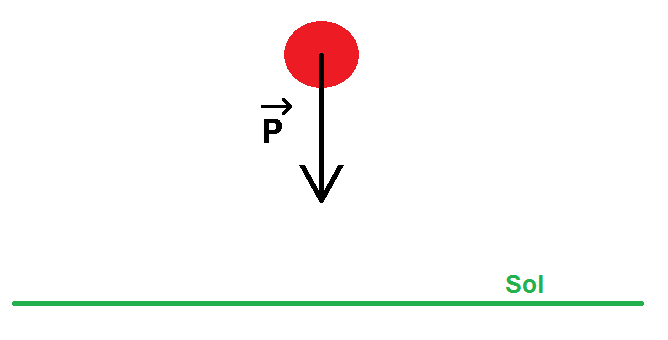
C’est quand même plus simple 
L’objet ne touche pas forcément le sol mais en tout cas il n’est pas très éloigné du sol (quelques dizaines de mètres).
—
ATTENTION !! Dans ce type de schéma on va souvent te donner un vecteur unitaire vertical, qui sera vers le haut ou vers le bas, et le sens de ce vecteur va déterminer si tu mets un signe moins ou non dans la formule, selon le schéma si-dessous :
—
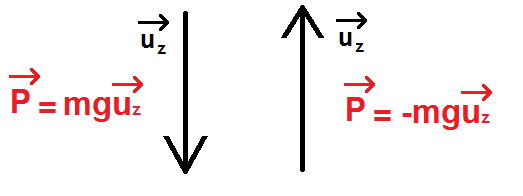
—
ATTENTION !!! Un point très important : on ne parle de poids que quand on a un objet à la surface de la Terre !!! (ou quelques dizaines de mètres au-dessus de la Terre). Ne parle jamais de poids entre deux planètes par exemple, ou entre deux astronautes dans l’espace.
Par contre le poids peut aussi se dire pour un objet sur la Lune ou toute autre planète.
—
En effet, on peut également parler de poids sur la Lune par exemple.
SAUF que le g n’est pas le même que sur la Terre ! En effet, reprenons la formule de g :
\(\textstyle g = \frac{G \times m_T}{(R_T)^2} \)
Ici on a mT et RT, mais s’il s’agit de la Lune, il faudra remplacer par la masse de la Lune et le rayon de la Lune pour trouver le g de la Lune, qur l’on peut noter gL :
\(\textstyle g_L = \frac{G \times m_L}{(R_L)^2} \)
Par contre le G est le même.
Si on est sur une autre planète c’est la même chose, mais encore une fois uniquement pour les objets proches de la surface de la planète.
Petite remarque avant de continuer : il arrive souvent que l’on étudie un satellite dans les exercices. On considère par exemple un satellite située à une hauteur h = 250 km de la surface de la Terre. Le schéma est donc le suivant :
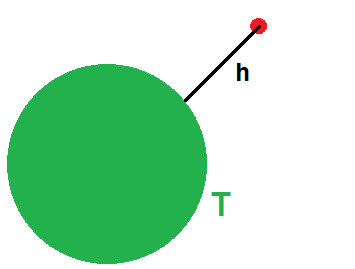
Ici hors de question de parler de poids, le satellite est bien trop loin de la Terre !!! On appliquera donc la formule de la force d’attraction gravitationnelle.
SAUF QUE, particularité ici, la distance d n’est pas h ! En effet d représente la distance entre le satellite et le CENTRE de la Terre. Donc d’après le schéma suivant, d = RT + h :
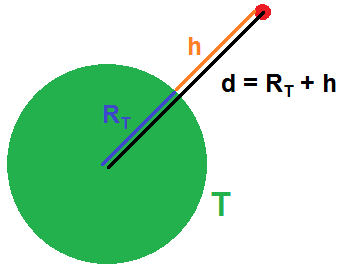
On aura donc comme formule, en notant S le satellite :
\(\textstyle \overrightarrow{F_{T/S}} = -G \frac{m_T \times m_S}{(R_T %2B h)^2} \overrightarrow{u_{TS}} \)
Retiens bien cet exemple car il arrive assez souvent.
Étudions maintenant un peu plus en détail ce g.
Tout d’abord quelle est son unité ? On peut la retrouver en faisant une analyse dimensionnelle de la formule, mais tu le feras tout seul pour t’entraîner, nous donnons ici uniquement le résultat  :
:
g est en m.s-2
Mais dis-donc, c’est la même unité que pour l’accélération non ?!
Et oui ! Et ce n’est pas pour rien si g s’appelle… l’accélération de la pesanteur ! Nous étudierons la raison de cette appellation dans le chapitre sur les équations horaires.
Et la valeur de g au fait ? Puisque c’est une constante on devrait avoir sa valeur non ?
En effet, nous allons pouvoir calculer la valeur à partir de la formule !
On rappelle que :
\(\textstyle g = \frac{G \times m_T}{(R_T)^2} \)
On a vu que RT = 6400 km environ soit 6400 x 103 m.
Et mT = 6,0 x 1024 kg environ (ceci est donné, tu n’as pas à l’apprendre)
D’où :
\(\textstyle g = \frac{6,67 \times 10^{-11} \times 6,0 \times 10^{24}}{(6400 \times 10^3)^2} \)
\(\textstyle g = 9,8 m.s^{-2} \)
On retrouve la valeur que tu as sûrement dû déjà voir dans les exercices, car la valeur de g est souvent donnée.
Parfois l’énoncé arrondit pour que les calculs soient plus simples (notamment si tu n’as pas de calculatrice) et donne g = 10 m.s-2, donc lis bien l’énoncé.
Et le g sur la Lune , combien vaut-il ? Si tu fais le calcul en cherchant la masse de la Lune et le rayon de la Lune dans ton livre (généralement dans le rabat de la couverture), tu trouveras :
gL = 1,6 m.s-2.
Qu’est-ce-que cela signifie ? Que la Lune t’attire moins vers « le bas » que la Terre, c’est pourquoi les astronautes peuvent rebondir à la surface de la Lune (mais ils finissent toujours par retomber car la force les attire quand même vers le bas).
Ainsi le poids sur la Lune est plus faible que celui sur la Terre.
« Mais alors, je pèse moins lourd sur la Lune que sur la Terre ? » te demandes-tu.
Oui et non ! En fait, le verbe « peser » vient en effet du mot poids. Comme le poids est plus faible sur la Lune, tu pèses en effet moins que sur la Terre. Mais ta MASSE reste la même !!!!
En fait, dans le langage courant on dit « je pèse … kilos », mais c’est faux de dire ça !! En effet, on a vu que le poids était une force, donc en Newton et non en kilos, c’est la masse qui est en kilos.
Tu devrais donc dire « ma masse est de … kilos » et non « je pèse … kilos », sauf que ce n’est pas très joli 
Il existe des exercices jouant sur cette subtilité, notamment en te demandant ce qui change ou ne change pas sur Terre et sur la Lune.
—
Tu dois retenir que la masse d’un objet ou d’une personne (en kilos) ne change pas s’il est sur Terre ou sur la Lune, mais son poids (en Newton) change car le g n’est pas le même.
—
Pour terminer sur g, mentionnons que parfois on parle du vecteur g. En fait, c’est juste qu’on a rentré le vecteur unitaire dirigé vers le bas (vers le sol) avec g :
\(\displaystyle \overrightarrow{g} = g\overrightarrow{u_z} \)
où uz est un vecteur unitaire dirigée vers le bas
Ainsi, on a une autre expression du vecteur P (sans signe moins car g est dirigé vers le bas, comme P) :
\(\displaystyle \overrightarrow{P} = m\overrightarrow{g} \)
Voyons maintenant une force ressemblant fortement à tout ce que l’on vient de voir : la force électrostatique.
La force électrostatique est présente entre deux charges électriques (par exemple des protons, des électrons…) chargées positivement ou négativement. On va considérer deux charges A et B séparées d »une distance d, et on va noter qA et qB les charges de A et B. On a ainsi le schéma suivant :
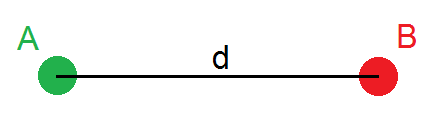
(Oui c’est le même que tout à l’heure mais là ce sont des charges et non des planètes^^)
L’expression de la force électrostatique exercée par A sur B est la suivante :
\(\displaystyle \overrightarrow{F_{A/B}} = k \frac{q_A \times q_B}{d^2} \overrightarrow{u_{AB}} \)
Comme tu le vois l’expression est très similaire à trois différences près.
Tout d’abord le G a été remplacé par une autre constante : k, appelé constante de Coulomb, avec k = 9,0 x 109 N.m2.C-2 (à ne pas retenir évidemment, le C c’est pour Coulomb).
Ensuite, les masses ont été remplacées par les charges (en Coulomb).
Mais la plus grosse différence est dans le fait qu’il n’y ait pas de signe moins !!!!
Par contre on a toujours le vecteur uAB, et d est toujours en mètres. On peut également ajouter que FA/B s’applique toujours en B et FB/A s’pplique toujours en A.
On va voir que ceci est très logique.
En effet, à la différence de la force d’attraction universelle qui est toujours une force attractive (comme son nom l’indique), la force électrostatique peut être répulsive.
Par exemple, si tu prends deux aimants, et que tu essayes d’approcher les deux pôles négatifs l’un vers l’autre, tu vas avoir du mal à cause de la force électrostatique qui repousse chaque aimant. De même si tu essayes d’approcher les deux pôles positifs.
Par contre si tu essayes d’approcher le pôle positif de l’un et le pôle négatif de l’autre, là au contraire ils vont naturellement s’attirer l’un vers l’autre grâce à la force électrostatique !
Ainsi, si les deux charges sont de même signe, la force devrait être répulsive, mais attractive si les charges ont des signes contraires.
Vérifions cela par le calcul :
1er cas : les charges qA et qB sont de même signe (toutes les deux positives ou toutes les deux négatives).
A ce moment-là qA x qB est positif.
Donc FA/B est selon uAB, et de même FB/A est selon uBA. Ce qui nous donne le schéma suivant :
Et là on voit clairement que les forces sont répulsives !
2ème cas : les charges qA et qB sont de signe opposé (qA négative et qB positive, ou l’inverse ça revient au même).
A ce moment-là qA x qB est négatif.
Donc FA/B est selon uBA, et de même FB/A est selon uAB. Ce qui nous donne le schéma suivant :

Et là on voit clairement que les forces sont attractives !
Le calcul confirme donc bien le principe selon lequel les contraires s’attirent : deux charges de signe opposé s’attirent, alors que deux charges de même signe se repoussent.
Retiens bien les ressemblances et encore plus les différences entre la force d’attraction gravitationnelle et la force électrostatique, surtout le fait que cette dernière n’a pas de signe moins dans sa formule !!
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !



Un très grand merci pour ces explications que je cherchai depuis des mois. J’aime l’astronomie et cela va beaucoup m’aider à comprendre ce qui est écrit dans les livres notamment le livre astrophysique et astronomie de Villeneuve.
Vos explications, c’est vraiment du pain béni pour moi. Merci, Merci, Merci……….
Merci beaucoup !
Bonjour,
Dans la partie poids, il est dit que « u(en gras) le vecteur unitaire dirigée de l’objet vers le centre de la Terre » or vous écrivez la formule de F t/a avec -u. Et u(en gras) est dirigée de l’ objet vers le centre de la terre. F t/a qui est, si je ne me trompe pas, le vecteur de la force exercée par la terre sur un objet (ayant une masse) situé à sa surface est un vecteur force qui est dirigée de l’objet vers le centre de la terre. Dans ce cas là ne faudrait-il pas écrire F t/a avec u(en gras) et F a/t avec -u(en gras).
Mon professeur de physique-chimie m’avait dit que la terre est soumise à la force F a/t mais que cela ne peut pas s’observer car la terre ayant une masse très grande cette force n a quasiment aucun effet sur elle.
Un énorme merci pour votre conception de ce site qui nous permet de réviser tranquillement à la maison.
En effet petite erreur j’ai changé en disant que u est dirigé du centre de la Terre vers l’objet, si tu as remarqué cette erreur c’est que tu as compris ! 🙂
Merci beaucoup pour ton commentaire et bon courage pour les révisions !
De rien et Merci
UN GRAND MERCI!!!!! ca m’a bcp aidé pour les révisions!!! même si c’était pas si dur que ca, c’était un peu flou mais la tout va mieux …… merci!