Sommaire
Introduction
Système masse-ressort horizontal
Système masse-ressort vertical
Pendule simple
Aspect énergétique
Oscillateur amorti
Exercices
Nous allons voir dans ce chapitre les oscillateurs harmoniques, dans un premier temps sans amortissement puis dans un second temps avec. Nous ne verrons ici que les oscillateurs harmoniques en mécanique mais il en existe dans d’autres chapitres (notamment en électricité avec les circuits LC).
Nous étudierons pour cela des exemples qui sont considérés comme du cours (donc à savoir refaire par coeur !). Tu pourras avoir à résoudre des exercices similaires mais avec des variantes, le principe de base restera le même.
Dans tout le chapitre nous étudierons les dérivées temporelles premières et secondes, qui seront notées avec un ou deux points au-dessus pour simplifier : il s’agit d’une notation très fréquente en physique :
\(\textstyle \frac{dx}{dt} = \dot{x} \)
\(\textstyle \frac{d^2x}{dt^2} = \ddot{x} \)
Nous profiterons de ce cours pour faire un rappel sur la force d’un ressort, au cas où tu ne l’aurais pas vu dans un autre chapitre.
Dans tout ce qui suit, certains vecteurs seront notés en gras pour plus de simplicité.
Enfin, nous aurons à résoudre des équations différentielles tout au long du chapitre, il est donc fortement recommandé de bien maîtriser la résolution d’équations différentielles avant d’aborder le chapitre ci-dessous.
Commençons donc par l’exemple le plus simple : le système masse-ressort horizontal.
Le système masse-ressort horizontal est très simple : on considère un ressort de longueur à vide l0 et de raideur k, accroché à un point fixe à son extrémité gauche, et à un objet de masse m à son extrémité droite (l’objet est parfois appelé masse) :
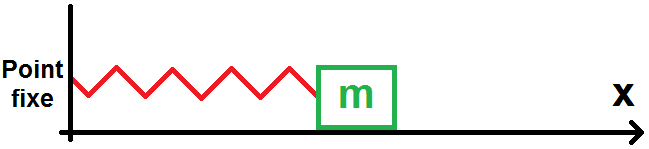
On prend l’axe (0x) dirigé vers la droite (de vecteur unitaire ux), et on cherche à savoir le mouvement de la masse. On va pour cela trouver l’équation différentielle de la position de l’objet et la résoudre.
La position de l’objet est repérée par son abscisse x sur l’axe.
On néglige les frottements dans un premier temps (le cas avec frottements sera vu plus tard dans le cours).
On applique donc la deuxième loi de Newton au système {masse} dans le référentiel du laboratoire.
Le système est soumis à son poids, à la réaction du support, et à la force du ressort appelée force de rappel.
La force de rappel notée F a pour expression :
\(\displaystyle \vec{F}_{ressort} = -k(l – l_0) \overrightarrow{u_{ext}} \)
Dans cette formule :
k est la raideur du ressort en N.m-1 (plus un ressort est « dur », plus k est grand)
l est la longueur du ressort (variable au cours du temps) en m
l0 est la longueur à vide du ressort en m
uext est un vecteur unitaire partant du milieu du ressort et allant vers l’extrémité où se situe le système. Ext signifie extérieur : le vecteur unitaire est dirigé du centre du ressort vers le système (donc vers l’extérieur du ressort).
Dans notre exemple, uext = ux
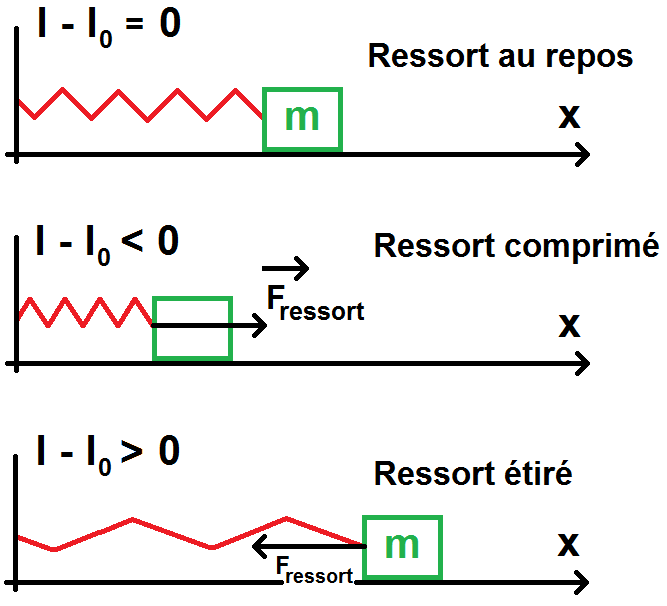
Le l-l0 correspond à ce que l’on appelle l’élongation du ressort, c’est-à-dire de combien il a été étiré ou au contraire comprimé par rapport à sa longueur à vide.
Le – devant le k vient du fait que si l – l0 > 0 : le ressort est étiré et va donc chercher à revenir à sa position initiale, la force est donc dirigée selon –uext.
Si au contraire l – l0 < 0 : le ressort est comprimé et va donc chercher à revenir à sa position initiale, la force est donc dirigée selon uext (-(l – l0) > 0) :
Appliquons donc la deuxième loi de Newton au système :
\(\textstyle m\vec{a} = \vec{P} + \vec{R} + \vec{F} \)
Le mouvement se faisant uniquement selon l’axe (Ox), on projette selon cet axe :
\(\textstyle m\ddot{x} = F \)
\(\textstyle m\ddot{x} = -k(l – l_0) \)
Dans cette équation, on rappelle que l est variable, il faut donc exprimer l en fonction de x.
Quand il est au repos, le ressort n’est ni allongé ni étiré (la masse n’applique aucune force), donc au repos l = l0.
On prend donc comme origine du repère la position à l’équilibre de la masse, situé à une distance l0 du point fixe :
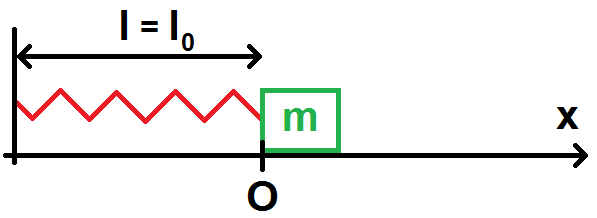
L’origine du repère ne coïncide pas ici avec le centre de la masse mais si on considère cette masse ponctuelle alors c’est le cas.
Cette technique de prendre la position d’équilibre comme origine du repère sera utilisée à chaque fois afin de simplifier les calculs (nous verrons après pourquoi). Retiens donc que :
—
On prend la position d’équilibre comme origine du repère afin de simplifier les calculs.
—
Voyons que vaut l lorsque le ressort n’est plus dans sa position d’équilibre :
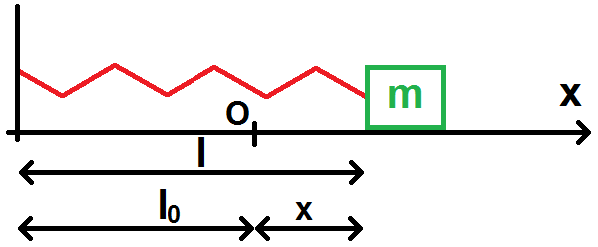
On voit facilement que l = l0 + x, donc l – l0 = x.
En remplaçant dans l’équation trouvée précédemment :
\(\textstyle m\ddot{x} = -kx \)
\(\textstyle m\ddot{x} + kx = 0 \)
On divise par m pour que le coefficient dominant soit 1 :
\(\textstyle \ddot{x} + \frac{k}{m}x = 0 \)
On vient de trouver l’équation différentielle régissant x !
On remarque que cette équation n’a pas de dérivée première, ce qui est normal car cela correspondrait à des frottements, qui ici sont négligés (nous verrons cela en détail dans la partie avec frottements).
Le coefficient devant x correspond au carré de la pulsation propre, notée ω0, en rad.s-1.
\(\displaystyle \ddot{x} + \omega_0^2 x = 0 \)
Il s’agit de l’équation différentielle qu’on obtiendra pour tous les oscillateurs harmoniques sans frottement. L’expression de ω0 variera évidemment en fonction du système étudié, et le x pourra être une autre variable (la variable donnant la position du système, comme y, z ou θ par exemple).
Pour notre exemple, par identification, on a :
\(\displaystyle \omega_0 = \sqrt{\frac{k}{m}} \)
pulsation d’un système masse ressort
On peut vérifier aisément que cette formule est homogène (nous le ferons dans les exercices en vidéo mais tu peux t’entraîner à le faire  ).
).
Une fois que l’on a trouvé l’équation différentielle, il faut la résoudre !
D’après ce que l’on a vu dans le chapitre sur les équations différentielles, on a :
\(\displaystyle x(t) = Acos(\omega_0 t) + Bsin(\omega_0 t) \)
ou bien :
\(\displaystyle x(t) = Ccos(\omega_0 t + \phi) \)
Nous avions vu en effet que l’on peut exprimer la solution avec cos et sin (il faut alors trouver les constantes A et B) ou bien uniquement avec cos (et il faut alors trouver C et φ).
Dans les deux cas, les constantes se trouveront avec les conditions initiales données dans l’énoncé. Comme il y a 2 constantes, il faudra deux conditions initiales (souvent la position et la vitesse).
Imaginons que l’on te dise qu’à t = 0 on écarte la masse de xm par rapport à sa position au repos et qu’on la lâche sans vitesse initiale.
On a donc x(0) = xm et v(0) = 0.
Voyons comment trouver les constantes dans les 2 cas.
Tout d’abord si x(t) = Acos(ω0t) + Bsin(ω0t).
x(0) = Acos(0) + Bsin(0) = A
Donc xm = A : facile !
Ensuite pour avoir la vitesse il faut dériver x :
\(\textstyle v(t) = \dot{x} \)
\(\textstyle v(t) = -\omega_0 Asin(\omega_0 t) + \omega_0 B cos(\omega_0 t) \)
D’où v(0) = -ω0Asin(0) + ω0Bcos(0) = ω0B
0 = ω0B
Comme ω0 ≠ 0, on en déduit B = 0.
On a donc x(t) = xmcos(ω0 t).
Voyons ce que cela donne avec l’autre expression : x(t) = Ccos(ω0 t + φ).
On a toujours x(0) = xm et v(0) = 0.
x(0) = Ccos(ω0 × 0 + φ) = Ccos(φ)
Donc xm = Ccos(φ) : c’est déjà moins bien car xm s’exprime en fonction des 2 variables…
On calcule la vitesse :
\(\textstyle v(t) = \dot{x} \)
\(\textstyle v(t) = -\omega_0 Csin(\omega_0 t + \phi) \)
D’où v(0) = -ω0Csin(ω0 × 0 + φ) = -ω0Csin(φ).
0 = -ω0Csin(φ).
Comme ω0 ≠ 0, C = 0 ou sin(φ) = 0.
Si C = 0, x(t) = 0 pour tout t : impossible ! (cela signifierait que la masse ne bouge pas du tout).
Donc sin(φ) = 0, donc φ = 0 modulo π : on prend φ = 0.
Or xm = Ccos(φ) = Ccos(0) = C.
D’où x(t) = xmcos(ω0 t) : on retrouve évidemment la même expression que précédemment !
Les calculs sont légèrement plus compliqués avec C et φ, il est donc recommandé de prendre la formule avec A et B si tu as le choix.
Traçons la forme de la solution trouvée :
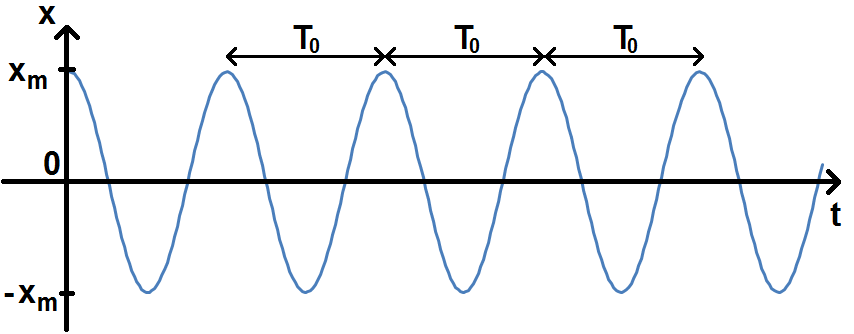
La période des oscillations, appelé période propre et notée T0, est définie par :
\(\displaystyle T_o = \frac{2 \pi}{\omega_0} \)
\(\displaystyle T_o = 2 \pi \sqrt{\frac{m}{k}} \)
L’interprétation est simple : la masse va osciller entre -xm et xm, donc autour de 0 qui est la position d’équilibre.
T0 correspond au temps que met la masse pour faire un aller-retour entre -xm et xm.
xm correspond donc à l’amplitude des oscillations.
Logique car on a écarté initialement la masse de xm, sans vitesse initiale, et comme il n’y a pas de frottement l’amplitude ne va pas diminuer, la masse fera donc des allers-retours entre -xm et xm.
Tu vois donc tout l’intérêt d’avoir pris la position d’équilibre comme origine de l’axe : comme le système oscillera toujours autour de sa position d’équilibre, en prenant celle-ci comme origine, le système oscillera toujours autour de 0.
L’autre intérêt est calculatoire. En effet, imaginons que l’on ait pris le point fixe comme origine :
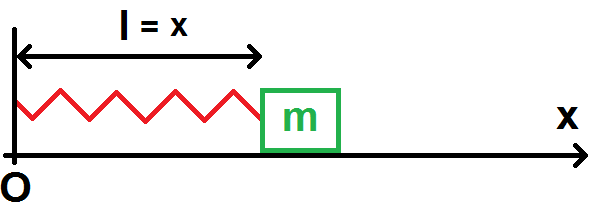
On a ainsi l = x.
Reprenons l’équation différentielle :
\(\textstyle m\ddot{x} = -k(l – l_0) \)
l = x donc :
\(\textstyle m\ddot{x} = -k(x – l_0) \)
\(\textstyle m\ddot{x} = -kx + kl_0 \)
\(\textstyle m\ddot{x} + kx = kl_0 \)
\(\textstyle \ddot{x} + \frac{k}{m}x = \frac{k}{m}l_0 \)
On retrouve l’équation différentielle précédente mais cette fois-ci avec un second membre : la résolution est donc plus longue !!
Ce principe vaudra pour tous les autres exemples :
—
Prendre la position d’équilibre comme origine permet d’obtenir une équation différentielle sans second membre.
—
C’est ce que nous allons voir tout de suite avec le deuxième exemple : le système masse-ressort vertical.
On prend le même ressort et la même masse que précédemment mais on attache cette fois-ci le ressort au plafond.
On prend l’axe (Ox) vertical dirigé vers le bas :
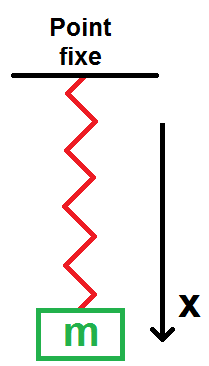
L’axe est pris vers le bas afin que uext corresponde là encore à ux.
L’étude sera fortement similaire à ce que l’on a fait précédemment sauf pour la position d’équilibre.
En effet, quand le ressort est horizontal, la position d’équilibre correspond à la longueur à vide (car pas de force appliquée au ressort).
Mais en vertical, le ressort est soumis à une force qui tire la masse vers le bas (correspondant au poids de la masse) : la longueur du ressort à l’équilibre, notée léq, ne sera donc pas égale à l0.
Commençons donc par déterminer léq.
On applique la deuxième loi de Newton à la masse à l’équilibre :
\(\textstyle \vec{P} + \vec{F} = \vec{0} \)
Vecteur nul car on est à l’équilibre.
\(\textstyle mg\vec{u_x} -k(l_{eq} – l_0) \vec{u_x} = \vec{0} \)
On projette sur ux :
\(\textstyle mg -k(l_{eq} – l_0) = 0 \)
\(\textstyle l_{eq} = l_0 + \frac{mg}{k} \)
On prend alors comme tout à l’heure l’origine de (Ox) au niveau de léq, c’est-à-dire à une distance l0 + mg/k du plafond :
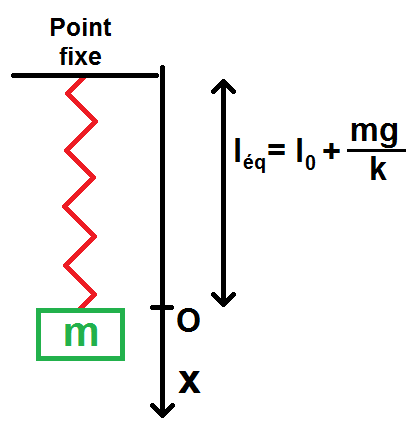
On a alors l = léq + x.
Appliquons maintenant la deuxième loi de Newton à la masse au cours de son mouvement :
\(\textstyle m\vec{a} = \vec{P} + \vec{F} \)
On projette sur (Ox) :
\(\textstyle m\ddot{x} = mg -k(l – l_0) \)
\(\textstyle m\ddot{x} = mg -k(l_{eq} + x – l_0) \)
\(\textstyle m\ddot{x} + kx = mg -kl_{eq} + k l_0 \)
D’après l’expression de léq trouvée précédemment, le membre de droite se simplifie !!
\(\textstyle m\ddot{x} + kx = 0 \)
\(\textstyle \ddot{x} + \frac{k}{m}x = 0 \)
On retrouve la même équation que pour le ressort horizontal : c’est normal, on trouvera toujours cette équation si on prend l’origine du repère au niveau de la position d’équilibre, cela permet comme on vient de le voir « d’annuler » le second membre de l’équation différentielle.
La résolution est alors identique au cas du ressort horizontal donc nous n’allons pas la refaire.
On remarque que l’on retrouve la même pulsation propre ω0, car on a le même système masse-ressort.
Voyons maintenant un autre système tout aussi classique mais avec des calculs différents : le pendule simple.
Le système du pendule simple est le suivant : on attache au plafond un fil inextensible de longueur l (inextensible signifie que la longueur l est constante).
Au bout de ce fil on accroche une masse m.
Le mouvement sera évidemment circulaire, on va donc repérer la position de l’objet avec les coordonnées polaires : on note donc θ l’angle entre l’axe vertical et le fil :
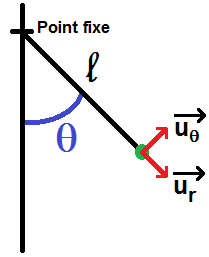
La position de la masse étant définie par l’angle θ, on va chercher l’équation différentielle régissant cette variable.
La position d’équilibre correspond évidemment à θ = 0, ce pourquoi on prend θ entre l’axe vertical et le fil.
La masse est soumise à son poids et la tension du fil notée T :

On voit que T est dirigée selon le vecteur –ur.
On applique alors la deuxième loi de Newton à la masse :
\(\textstyle m\vec{a} = \vec{P} + \vec{T} \)
D’après ce que l’on a vu sur les coordonnées polaires, on a :
\(\textstyle \vec{a} = (\ddot{l} – l\dot{\theta}^2)\vec{u_r} + (2\dot{l}\dot{\theta} + l\ddot{\theta})\vec{}u_{\theta} \)
Le fil étant inextensible :
\(\textstyle \dot{l} = \ddot{l} = 0 \)
D’où :
\(\textstyle \vec{a} = – l\dot{\theta}^2\vec{u_r} + l\ddot{\theta}\vec{u_{\theta}} \)
On exprime également P et T selon ur et uθ, ce qui donne en remplaçant dans la deuxième loi de Newton :
\(\textstyle m(- l\dot{\theta}^2\vec{u_r} + l\ddot{\theta}\vec{u_{\theta}}) = mgcos(\theta)\vec{u_r} – mgsin(\theta)\vec{u_{\theta}}-T\vec{u_r} \)
Comme on ne connaît pas la valeur de T, on projette sur uθ :
\(\textstyle ml\ddot{\theta} = -mgsin(\theta) \)
\(\textstyle \ddot{\theta} + \frac{g}{l}sin(\theta) = 0 \)
On se place dans l’approximation des petits angles, donc sin(θ) ≈ θ, d’où :
\(\textstyle \ddot{\theta} + \frac{g}{l}\theta = 0 \)
On retrouve encore une fois l’équation différentielle harmonique !
Le ω0 est ici évidemment différent du système masse-ressort, on a :
\(\displaystyle \omega_0= \sqrt{\frac{g}{l}} \)
\(\displaystyle T_0= 2\pi\sqrt{\frac{l}{g}} \)
Tu peux t’entraîner à vérifier l’homogénéité de ces formules 
Là encore la suite de la résolution est similaire à ce que l’on a fait précédemment.
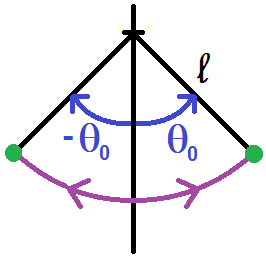
Si on écarte initialement le fil d’un angle θ0 et qu’on le lâche sans vitesse initiale, on trouve :
θ = θ0cos(ω0t) : la masse va osciller autour de la position d’équilibre θ = 0, entre θ0 et -θ0 :
Tout ce que l’on a vu depuis le début peut également se retrouver grâce à une étude énergétique.
Pour trouver l’équation différentielle, on a appliqué la deuxième loi de Newton.
Mais on pourrait également utiliser l’énergie.
En effet, reprenons notre système masse-ressort horizontal.
Comme on néglige les frottements, l’énergie mécanique est constante. L’idée est donc d’exprimer cette énergie mécanique et de dire que sa dérivée temporelle est nulle puisqu’elle est constante.
L’énergie mécanique est ici constituée de l’énergie cinétique Ec et de l’énergie potentielle élastique Epe. Il y a également de l’énergie potentielle de pesanteur, mais la hauteur ne variant pas, on la prend nulle au niveau du système.
On sait que x = l – l0, donc Epe a pour expression :
\(\textstyle E_{pe} = \frac{1}{2}k(l – l_0)^2 = \frac{1}{2}kx^2 \)
L’énergie cinétique est :
\(\textstyle E_c = \frac{1}{2}mv^2 = \frac{1}{2}m\dot{x}^2 \)
D’où :
\(\textstyle E_m = E_c + E_{pe} \)
\(\textstyle E_m = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}kx^2 \)
L’énergie mécanique étant constante :
\(\textstyle \frac{dE_m}{dt} = 0 \)
Ainsi :
\(\textstyle \frac{1}{2}m \times 2\ddot{x}\dot{x} + \frac{1}{2}k \times 2\dot{x}x = 0 \)
En simplifiant :
\(\textstyle \ddot{x} + \frac{k}{m}x = 0 \)
On retrouve l’équation différentielle harmonique trouvée grâce à la deuxième loi de Newton.
Si tu préfères cette méthode c’est tout à fait possible, tu peux t’entraîner à le faire pour le ressort vertical et le pendule, les calculs sont un peu plus compliqués 
Une fois l’équation différentielle trouvée, la suite du raisonnement est identique à ce que l’on a fait auparavant.
Par ailleurs, il est également important de comprendre les transferts d’énergie ayant lieu au cours du mouvement.
En effet, l’énergie mécanique est constante, mais l’énergie potentielle se transforme en énergie cinétique et réciproquement.
Si on prend le pendule simple par exemple, lors de la descente, l’énergie potentielle de pesanteur va diminuer et l’énergie cinétique augmenter : l’énergie potentielle se transforme en énergie cinétique !
Lors de la montée ce sera l’inverse.
On aura alors un graphique ressemblant à ça :
Le détail de l’étude énergétique a déjà été détaillé dans le chapitre sur l’énergie mécanique, tu es donc invité à aller l’étudier pour plus de détails sur les échanges énergétiques au cours du mouvement.
On a dit que l’énergie mécanique était constante à cause de l’absence de frottements.
Voyons donc maintenant ce qu’il se passe avec les frottements.
On reprend le système masse ressort horizontal mais on considère maintenant qu’il y a des frottements, modélisés par une force de frottement fluide f, proportionnelle à la vitesse :
\(\textstyle \vec{f} = -\alpha\vec{v} \)
Le – vient du fait que la force de frottement est opposée au mouvement donc à la vitesse.
α est un coefficient de frottement (α = 0 si on néglige les frottements).
v étant la dérivée de x :
\(\textstyle \vec{f} = -\alpha\dot{x}\vec{u_x} \)
Appliquons la deuxième loi de Newton à la masse :
\(\textstyle m\vec{a} = \vec{P} + \vec{R} + \vec{F} + \vec{f} \)
On projette sur l’axe (Ox) :
\(\textstyle m\ddot{x} = -kx – \alpha\dot{x} \)
\(\textstyle m\ddot{x} + \alpha\dot{x} + kx = 0 \)
\(\textstyle \ddot{x} + \frac{\alpha}{m}\dot{x} + \frac{k}{m}x = 0 \)
On voit qu’il y a une différence avec l’équation d’un système non amorti : la présence de la dérivée première de x, dont le coefficient dépend de α.
Si α = 0, on retrouve l’équation d’un système harmonique (normal car à ce moment-là il n’y a pas de force de frottement).
On peut donc dire que :
—
La dérivée première de la position dans l’équation différentielle traduit la présence de frottements.
—
On remarque que le coefficient de x est le même que précédemment, on reprend donc le même ω0.
Pour le coefficient de la dérivée première, nous avons 3 possibilités, et pour chacune nous allons introduire un nouveau facteur.
1) On introduit le facteur λ, en s-1, défini par :
\(\displaystyle \lambda = \frac{\alpha}{2m} \)
Nous verrons plus loin l’intérêt du 2.
On a alors :
\(\displaystyle \ddot{x} + 2\lambda \dot{x} + \omega_0^2x = 0 \)
2) On introduit une constante de temps τ, en s, définie par :
\(\displaystyle \tau = \frac{m}{\alpha} = \frac{1}{2 \lambda} \)
λ étant en s-1, τ est bien en s.
L’équation différentielle devient alors :
\(\displaystyle \ddot{x} + \frac{1}{\tau} \dot{x} + \omega_0^2x = 0 \)
3) 3ème possibilité : on introduit le facteur de qualité Q, sans unité, défini par :
\(\displaystyle Q = \omega_0 \tau \)
ω0 étant en rad.s-1, et τ en s, Q est bien sans unité.
L’équation différentielle s’écrit alors :
\(\displaystyle \ddot{x} + \frac{\omega_0}{Q} \dot{x} + \omega_0^2x = 0 \)
λ et Q sont utilisés en Sciences de l’ingénieur, τ un peu moins.
Suivant l’énoncé, tu devras utiliser plutôt l’un ou l’autre des facteurs. Attention à ne pas mélanger les facteurs et les expressions !
Ce qu’il te faudra surtout retenir c’est la résolution de ces équations différentielles, plus complexe que dans le cas harmonique.
En effet, nous avons vu dans le chapitre sur les équations différentielles que les solutions vont dépendre de la valeur du discriminant de l’équation caractéristique.
Pour comprendre la suite, il est impératif que tu maîtrises les équations différentielles d’ordre 2, sinon tu vas être perdu !
Calculons ce discriminant dans le 1er cas (celui avec λ).
L’équation caractéristique est :
\(\textstyle r^2 + 2\lambda r + \omega_0^2 = 0 \)
Le discriminant vaut :
\(\textstyle \Delta = (2\lambda)^2 – 4 \times \omega_0^2 \)
\(\textstyle \Delta = 4\lambda^2 – 4\omega_0^2 \)
\(\textstyle \Delta = 4(\lambda^2 – \omega_0^2) \)
\(\textstyle \Delta = 4(\lambda – \omega_0)(\lambda + \omega_0) \)
C’est là que tu vois tout l’intérêt d’avoir mis le 2 dans l’expression du facteur α : si on n’avait pas mis le 2, on n’aurait pas pu factoriser par 4, et donc pas pu simplifier Δ…
Or λ et ω0 sont positifs, donc λ + ω0 > 0.
Le signe de Δ dépend donc du signe de (λ – ω0).
On en déduit donc 3 cas :
1er cas : λ < ω0
On a donc Δ < 0 : régime pseudo-périodique.
On montre facilement que l’on a :
\(\displaystyle \Delta \lt 0 \Leftrightarrow \lambda \lt \omega_0 \Leftrightarrow Q \gt \frac{1}{2} \)
Les deux racines complexes sont :
\(\textstyle r_1 = \frac{-2\lambda – j\sqrt{4(\omega_0^2 – \lambda^2)}}{2} \)
\(\textstyle r_1 = \frac{-2\lambda – 2j\sqrt{\omega_0^2 – \lambda^2}}{2} \)
\(\textstyle r_1 = -\lambda – j\sqrt{\omega_0^2 – \lambda^2} \)
Et :
\(\textstyle r_2 = -\lambda + j\sqrt{\omega_0^2 – \lambda^2} \)
On pose alors une nouvelle constante ω, appelée pseudo-pulsation, correspondant à la partie imaginaire des racines, c’est-à-dire :
\(\displaystyle \omega = \sqrt{\omega_0^2 – \lambda^2} \)
\(\displaystyle pseudo-pulsation \, \omega \)
Les deux racines s’expriment alors :
\(\textstyle r_{1,2} = -\lambda \pm j\omega \)
Les solutions de l’équation différentielles sont alors de la forme :
\(\textstyle x(t) = e^{-\lambda t}(Acos(\omega t) + Bsin(\omega t)) \)
A et B sont des constantes à déterminer.
Tu auras remarqué que contrairement au cas non-amorti, c’est ω et non plus ω0 qui est dans le cos et le sin : on aurait donc des oscillations à la pulsation ω et non pas ω0 (d’où l’intérêt d’avoir posé ω).
Le cos et le sin vont donner des oscillations, tandis que le exp(-λt) est une sorte d’amplitude, décroissante car -λ < 0.
On aura donc des oscillations dont l’amplitude diminue, c’est-à-dire des oscillations amorties :
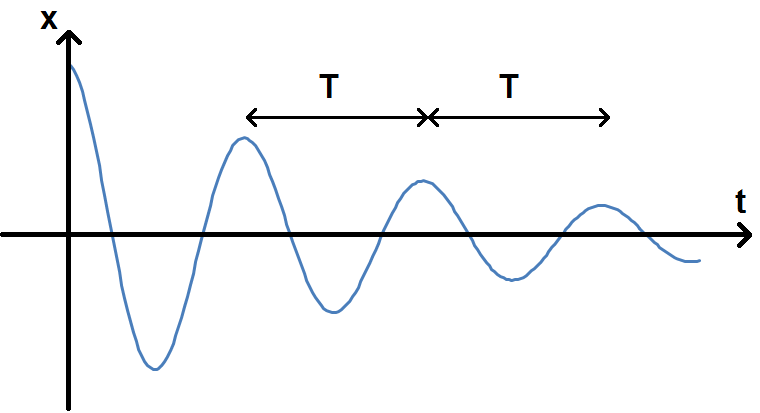
Les courbes exp(-λt) et -exp(-λt) forment une enveloppe à l’intérieur de laquelle la fonction va osciller à cause du cos :
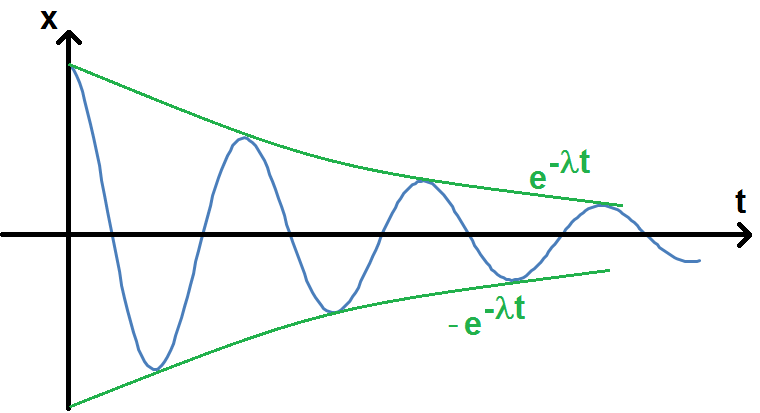
Plus λ est grand, plus les oscillations sont amorties, jusqu’à ce que λ soit égale à ω0 et que l’on passe en régime apériodique (c’est ce que nous verrons après).
On voit que les frottements ont pour effet de diminuer progressivement l’amplitude des oscillations jusqu’à ce qu’il n’y en ait plus.
Comme on a défini une pseudo-pulsation, on définit aussi la pseudo-période T = 2π/ω.
ω est appelé pseudo-pulsation car on a quand même une régularité temporelle dans les oscillations, de pseudo-période T, mais le phénomène n’est pas réellement périodique car l’amplitude n’est pas la même, d’où le terme de pseudo-pulsation et de régime pseudo-périodique.
La pseudo-période des oscillations est donc définie par :
\(\textstyle T = \frac{2\pi}{\omega} \)
\(\textstyle T = \frac{2\pi}{\sqrt{\omega_0^2 – \lambda^2}} \)
On montre alors facilement que :
\(\displaystyle T \gt T_0 \)
En pratique, la différence entre T et T0 est assez faible, mais T sera quand même plus grande que T0.
Remarque : s’il n’y a pas de frottement, α = 0, donc λ = 0 et alors ω = ω0 et T = T0 : on retrouve bien le cas non-amorti.
2ème cas : λ > ω0
On a donc Δ > 0 : régime apériodique.
On a :
\(\displaystyle \Delta \gt 0 \Leftrightarrow \lambda \gt \omega_0 \Leftrightarrow Q \lt \frac{1}{2} \)
Il y a deux racines réelles qui sont :
\(\textstyle r_1 = \frac{-2\lambda – \sqrt{4(\lambda^2 – \omega_0^2)}}{2} \)
\(\textstyle r_1 = \frac{-2\lambda – 2\sqrt{\lambda^2 – \omega_0^2}}{2} \)
\(\textstyle r_1 = -\lambda – \sqrt{\lambda^2 – \omega_0^2} \)
Et :
\(\textstyle r_2 = -\lambda + \sqrt{\lambda^2 – \omega_0^2} \)
On montre facilement que r1 et r2 sont négatives (entraînes-toi à le montrer !).
On sait que les solutions de l’équation différentielle sont alors :
\(\textstyle x(t) = Ae^{r_1t} + Be^{r_2t} \)
A et B sont des constantes à déterminer.
Il s’agit de deux exponentielles décroissantes (puisque r1 et r2sont négatives) : il n’y a pas d’oscillation :
On voit que plus λ est faible, plus la courbe est « basse » et tend rapidement vers 0 (donc vers l’équilibre). Le cas limite est le dernier cas que l’on va voir.
3ème cas : λ = ω0
On a donc Δ = 0 : régime critique.
On a :
\(\displaystyle \Delta = 0 \Leftrightarrow \lambda = \omega_0 \Leftrightarrow Q = \frac{1}{2} \)
Ce régime est celui qui permet au système de revenir le plus rapidement à l’équilibre. Son allure est la même que celle d’un régime apériodique vue ci-dessus.
Avant de terminer ce chapitre, faisons une dernière remarque sur les facteurs λ et Q.
On vient de voir que si λ est faible, et donc Q grand, on aura des oscillations pseudo-périodiques, à ce moment-là plus λ est faible moins l’amplitude décroîtra rapidement.
Le cas limite est λ = 0, donc Q = +∞, correspondant à une absence de frottement : λ est donc un facteur mesurant l’importance des frottements (normal car il est proportionnel à α).
A l’inverse, Q est appelé facteur de qualité : une grande qualité correspond à de faibles frottements : ce que l’on appelle un système « de grande qualité » est donc un système sans frottement (normal car on souhaite généralement minimiser les frottements).
Pour accéder aux exercices sur ce chapitre, clique ici !
Sommaire des coursHaut de la page



Merci beaucoup cela complete ce que j`ai pas fait en Terminale A¸
MERCI