Sommaire
Introduction
Formules de base
Projection d’un vecteur
Ce chapitre est un préambule au chapitre suivant sur les équations horaires. Ici on va voir les outils, notamment géométriques (il y aura de la trigo !!), qui vont te permettre de faire les exercices sur les équations horaires.
Remarque : dans ce chapitre (comme dans d’autres chapitres), certains vecteurs seront notés en gras, sans la flèche. Cette notation est parfois utilisée dans les énoncés donc cela va t’habituer à voir cette notation 
Pour ce chapitre il y a quelques formules à connaître.
Tout d’abord la 2ème loi de Newton que tu dois connaître et dont on rappelle la formule :
\(\displaystyle \sum\vec{F} = m \times \vec{a} \)
C’est la formule de base que l’on utilisera tout le temps pour commencer le calcul quand tu devras trouver l’équation de la trajectoire.
La seule force que l’on aura dans ce type d’exercices est le poids dont on rappelle la formule :
\(\displaystyle \vec{P} = m \times \vec{g} \)
En fait, à la place du vecteur g, on mettra plutôt g avec le vecteur vertical correspondant :
\(\displaystyle \vec{P} = – m \times g \, \vec{u_z} \)
\(\displaystyle si \, \vec{u_z} \, est \, vers \, le \, haut \)
\(\displaystyle \vec{P} = m \times g \, \vec{u_z} \)
\(\displaystyle si \, \vec{u_z} \, est \, vers \, le \, bas \)
—
ATTENTION !! Pense bien à regarder si le vecteur vertical est vers le haut ou vers le bas pour savoir si tu mets un – ou non.
—
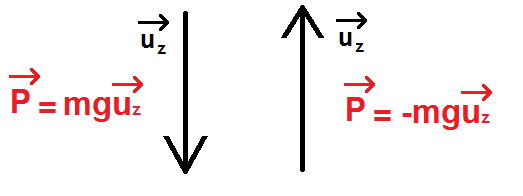
Remarque : on a pris uz comme exemple de vecteur vertical mais ça peut être ux ou uy.
Passons maintenant aux autres formules. Celles-ci vont permettre de relier l’accélération d’un objet (le vecteur a), à sa vitesse (le vecteur v) et à sa position (vecteur OM, car on considère un objet représente par un point M).
Tout d’abord on a :
\(\displaystyle \vec{a} = \frac{d\vec{v}}{dt} \)
—
ATTENTION ! Il s’agit d’une notation sûrement nouvelle pour toi.
Ce dv/dt ne signifie pas du tout d fois v divisé par d fois t !!
Il s’agit d’une notation pour exprimer le fait qu’on DÉRIVE v PAR RAPPORT à t.
C’est comme quand on note f'(x) : on dérive f par rapport à x :
\(\textstyle f'(x) = \frac{df}{dx} \)
\(\textstyle \frac{dv}{dt} = v'(t) \)
—
L’accélération est ainsi la dérivée de la vitesse par rapport au temps. Donc pour calculer l’accélération on dérive la vitesse.
Sauf que la plupart du temps on aura l’accélération et on voudra trouver la vitesse. Il faut donc faire l’inverse de la dérivée, c’est-à-dire… la primitive ! D’où l’intérêt d’avoir revu le chapitre sur les primitives 
—
ATTENTION !! Quand on fait une primitive en physique, on met toujours + constante.
En effet, les primitives sont toujours à une constante près. En maths la plupart du temps on ne la met pas car on dit qu’elle vaut 0, cela n’a pas d’influence sur l’exercice. Mais en physique cette constante est très importante car elle ne vaut pas toujours 0.
Nous insisterons de toute façon sur ce point quand on passera aux exercices.
—
—
Autre remarque importante : ici la variable est t, et non x comme souvent en maths.
Donc si on fait la primitive de 5 par exemple, ce sera 5t + constante, et non 5x + constante.
—
L’autre formule relie cette fois-ci la vitesse et la position. Le principe est le même :
\(\displaystyle \vec{v} = \frac{d\overrightarrow{OM}}{dt} \)
La vitesse est ainsi la dérivée de la position. Donc pour calculer la vitesse on dérive la position.
Sauf que la plupart du temps on aura la vitesse et on voudra trouver la position. Il faut donc comme précédemment faire l’inverse de la dérivée, c’est-à-dire la primitive.
Remarque : tu as peut-être remarqué que dans les formules on dérive des vecteurs. Ne t’inquiète pas de cela, en fait dans les exercices on va d’abord projeter le vecteur dans le repère avant de faire la primitive, donc tu n’auras jamais à faire directement la dérivée ou la primitive d’un vecteur.
Mais projeter un vecteur dans un repère, qu’est-ce-que c’est ?
Projeter un vecteur, ça veut dire donner ses coordonnées dans le repère. On aura uniquement des repères à 1 dimension ou 2 dimensions, pas 3 dimensions.
Au niveau des notations, quand on a un vecteur accélération dans un repère (x ; y) par exemple, ses composantes seront notées ax et ay.
Si on a un vecteur vitesse dans un repère (x ; z) par exemple, ses composantes seront notées vx et vz.
Pour le vecteur position dans un repère (x ; z) par exemple, ses composantes seront notées simplement x et z.
Bien sûr, si dans l’énoncé on te donne d’autres notations précises, tu utiliseras ces notations-là et non celles que l’on vient de voir.
—
Avant de passer aux exemples, il est important de noter que toutes ces variables dépendent du temps.
On devrait donc noter ax(t), az(t), v
Mais sur ta copie tu devras noter avec (t) (sauf si tu es pressé par le temps).
—
Passons maintenant aux exemples pour que tu voies concrètement ce qu’est la projection :
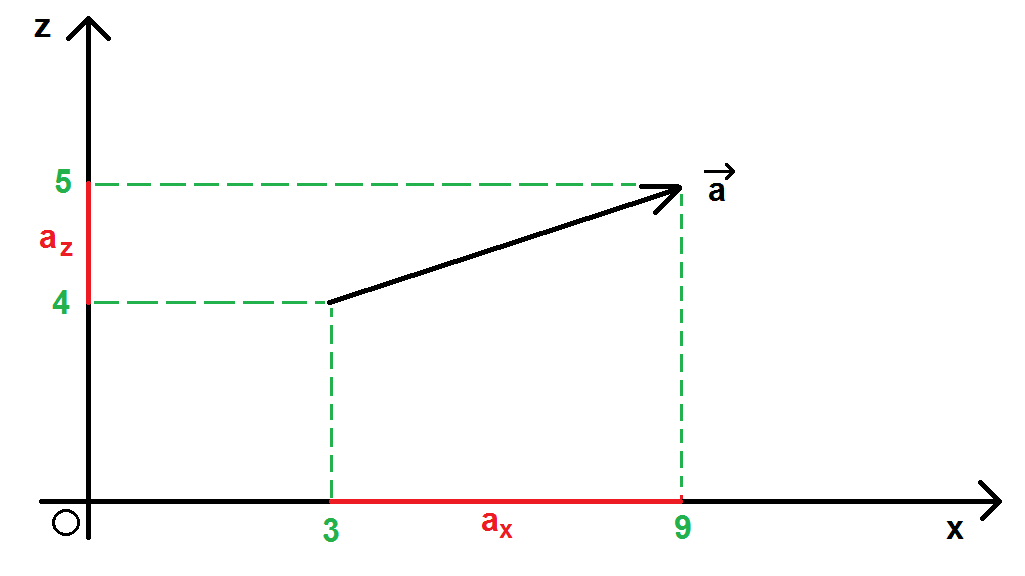
On a ici le vecteur a dans un repère (x ; z). On aura donc ax et az.
Sur l’axe x, le vecteur a pour abscisse 6 (9-3). Donc ax = 6
Sur l’axe z, le vecteur a pour abscisse 1 (5-4). Donc az = 1.
Et voilà ce n’est pas plus compliqué que ça !
Sauf que dans les exercices tu n’auras pas de chiffres mais des lettres…
Nous allons donc détailler ici l’exemple le plus classique que tu auras.
On a le schéma suivant :
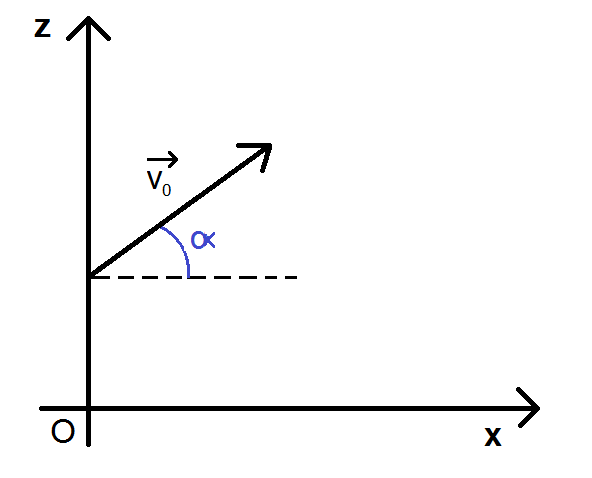
On a donc le vecteur v0 (le vecteur est souvent noté ainsi car c’est le vecteur initial, à t = 0), dans le repère (x ; z) qui fait un angle α avec l’horizontale (configuration la plus répandue dans les exercices). La norme de ce vecteur est notée v0 (sans vecteur).
Il a donc deux coordonnées v0x et v0z :
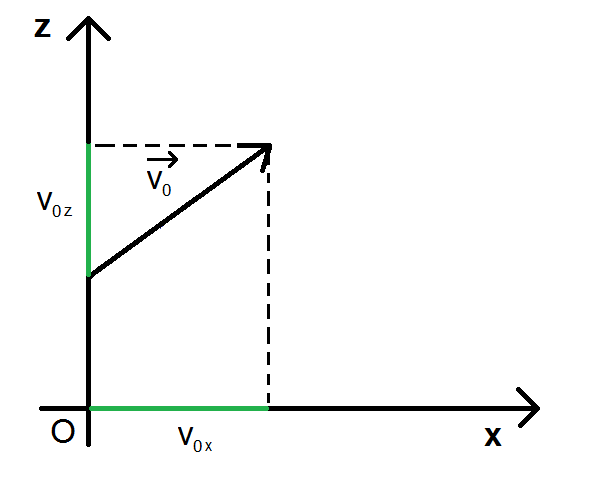
Ces coordonnées se retrouvent également ici :
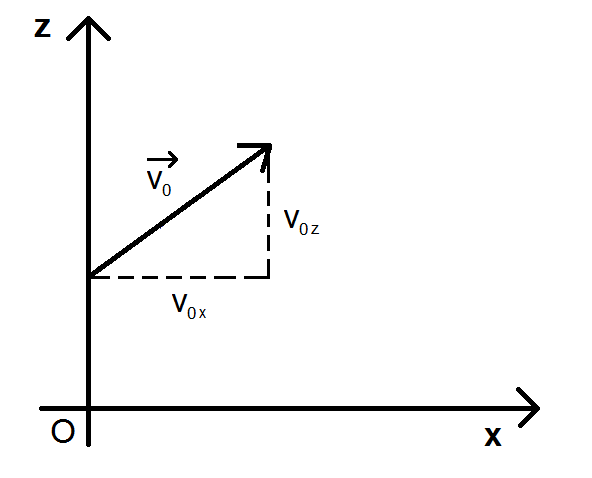
Et c’est là que la trigonométrie intervient. On va considérer le triangle rectangle en rouge :
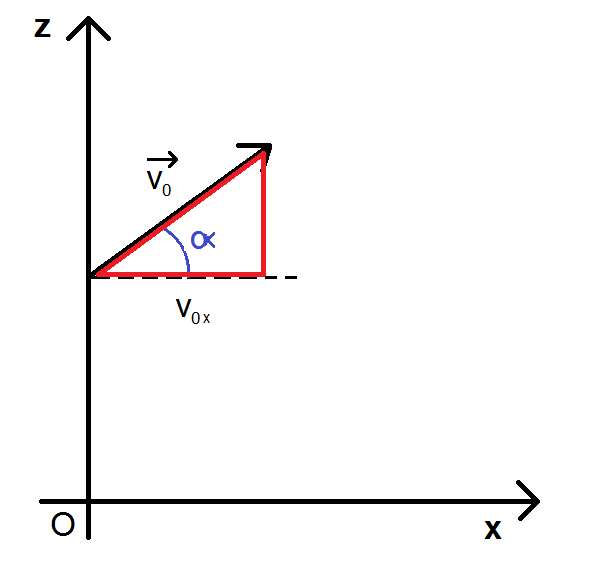
Dans ce triangle, on a :
\(\textstyle cos(\alpha) = \frac{v_{0x}}{v_0} \)
d’où
\(\textstyle v_{0x} = cos(\alpha) \times v_0 \)
Et voilà tout simplement !
De même, dans ce même triangle rectangle en rouge, il y a également v0z :
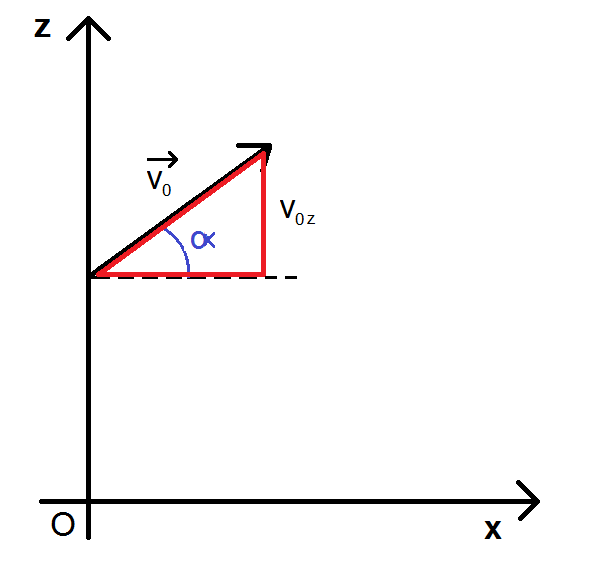
\(\textstyle sin(\alpha) = \frac{v_{0z}}{v_0} \)
d’où
\(\textstyle v_{0z} = sin(\alpha) \times v_0 \)
On a alors v0x et v0z.
Le principe est le même dans les configurations suivantes (mais les formules ne sont pas les mêmes, à toi de les trouver !) :
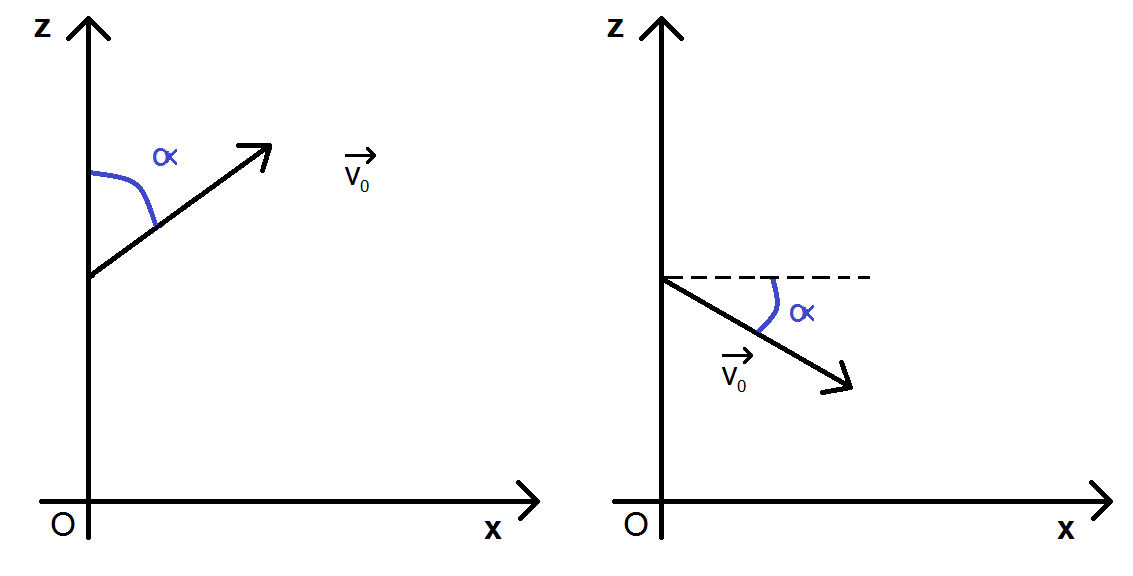
Comme tu le vois, rien d’exceptionnel si tu connais bien tes formules de trigo 
Une fois que tu as maîtrisé ce chapitre, on va pouvoir passer aux applications de tout cela et rentrer dans le vif du sujet dans le chapitre sur les équations horaires.



merci d’avoir creer ce site !!!
Bonjour j’aimerais savoir si vous avez les cours de prépa en physique comme pour les mathématiques
Oui il y a en a dans le menu « Cours de physique » et « Cours de chimie »
j’aimerais savoir comment fais pour savoir que c’est sin ou cos faut utiliser … sur quoi ce base t-on pour fais cela aidez moi s’il vous plaît ??
J’explique ça dans les exercices en vidéo !
Je tenais à vous remercier pour toute cette aide que vous nous apportez grâce à ce merveilleux site !
Je suis en TS et j’ai d’énorme difficultés en physique/chimie, je suis tombée sur votre site par hasard en cherchant de l’aide sur la mécanique, et vous avez réussi à m faire comprendre l’incompréhensible x)
J’ai également une petite idée pour une amélioration, si cela vous intéresse évidement. J’ai énormément de problème d’internet et donc j’imprime beaucoup « les pages de sites », et donc le texte du site mais aussi les pub, les commentaires etc…si vous pouviez mettre le texte sur un pdf je pense que cela servirait beaucoup à un grand nombre de monde 🙂
Encore merci et bonne continuation !
Merci beaucoup pour votre aide, elle m’est plutôt indispensable là….!
Excellent site👌🏽 Merci pour tout c’est vraiment génial ce que vous faite je pourrais dire que grâce à vous j’ai eu mon bacS alors que je travaille à la maison merci 🙏
Merci beaucoup, bon courage pour la suite ! 🙂
merci pour votre instruction