Sommaire
Introduction
Coordonnées cartésiennes
Coordonnées polaires
Changement de base et dérivée en polaires
Coordonnées cylindriques
Coordonnées sphériques
Exercices
Nous allons voir dans ce chapitre les différents repères que tu pourras rencontrer en Physique.
Il y en a 4, mais on verra que les coordonnées polaires et cylindriques sont très similaires.
Nous étudierons plus précisément les coordonnées polaires car c’est celui que tu rencontreras le plus et pour lequel il existe des formules de changement de base et de dérivation que tu auras souvent à utiliser.
Dans tout le chapitre, certains vecteurs seront notés en gras pour plus de simplicité.
Commençons par le plus simple et qui servira de base aux autres repères : les coordonnées cartésiennes.
Les coordonnées cartésiennes (O, x, y z) sont associées au repère orthonormé (O, ux, uy, uz). Le point O est le centre du repère.
Le repère est dit orthonormé car les trois vecteurs du repère sont orthogonaux entre eux et normés (c’est-à-dire de norme 1).
Tous les repères que nous étudierons sont d’ailleurs orthonormés.
On a ainsi :
\(\displaystyle \vec{u_x} \cdot \vec{u_y} = \vec{u_x} \cdot \vec{u_z} = \vec{u_y} \cdot \vec{u_z} = 0 \)
\(\displaystyle ||\overrightarrow{u_x}|| = ||\overrightarrow{u_y}|| = ||\overrightarrow{u_z}|| = 1 \)
Il en sera de même pour tous les vecteurs des repères que nous verrons.
Si un point M a pour coordonnées (a, b, c), on peut alors écrire :
\(\textstyle \overrightarrow{OM} = a\overrightarrow{u_x} + b\overrightarrow{u_y} + c\overrightarrow{u_z} \)
Ici l’expression est simple, pour les autres repères cela sera différent.
Le repère cartésien est cependant le seul dont les axes sont fixes : ils ne bougent pas au cours du mouvement du système contrairement aux autres.
On le trace de la manière suivante :
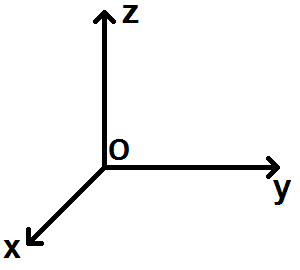
Evidemment il faut penser en 3D, les axes y et z forment un plan vertical, tandis que l’axe x vient vers toi.
Si tu as du mal à voir en 3D tu peux imaginer un carré, les axes sont alors les arêtes du fond comme sur ce schéma :
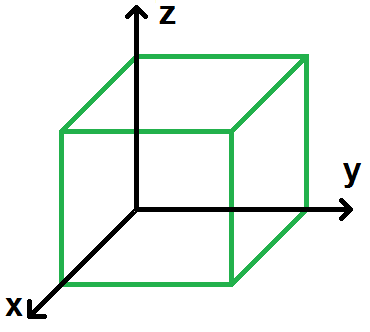
Mais comment savoir que x vient vers toi, y est vers la droite et z vers le haut ??
C’est là qu’intervient la règle du tire-bouchon, aussi appelé règle de la main droite.
Le principe est le suivant :
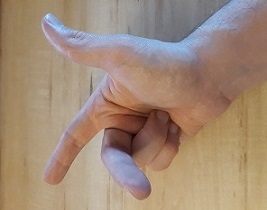
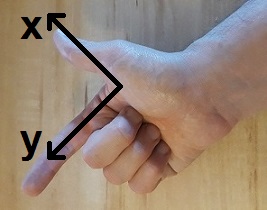
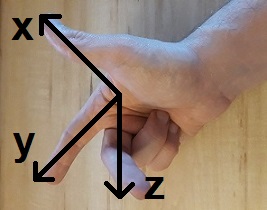
– commence par fermer le poing de la main droite (attention, surtout par la gauche car tu obtiendras l’inverse !!).
– commence par lever le pouce : il s’agit de l’axe x ;
– lève ensuite l’index (à côté du pouce) : il s’agit de l’axe y ;
– lève enfin le majeur : il s’agit de l’axe z.
Tu dois obtenir ça :
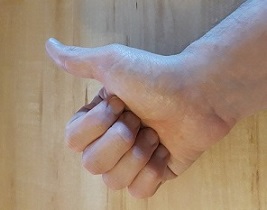
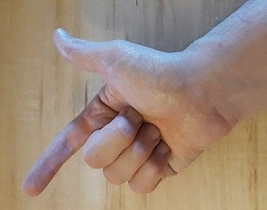

Si maintenant tu places ta main de façon à faire correspondre les axes du schéma ci-dessus avec tes doigts, tu vois où sont x, y et z :
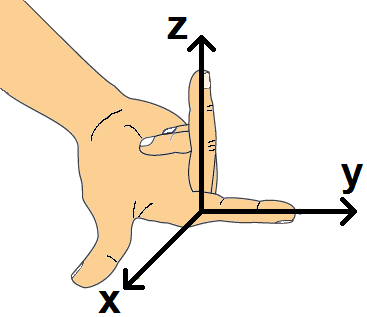
A noter que le repère peut être mis n’importe où dans l’espace, pas nécessairement au point O, cela ne change rien.
Le repère cartésien est surtout utilisé pour des mouvements rectilignes à 1 dimension, ou des mouvements quelconques.
Enfin, remarquons que dans le repère (O, ux, uy, uz), les vecteurs de la base ont pour coordonnées :
\(\displaystyle \overrightarrow{u_x} (1 \, ; \, 0 \, ; \, 0) \)
\(\displaystyle \overrightarrow{u_y} (0 \, ; \, 1 \, ; \, 0) \)
\(\displaystyle \overrightarrow{u_z} (0 \, ; \, 0 \, ; \, 1) \)
A partir de ces coordonnées, on va définir toutes les autres, notamment les coordonnées polaires.
Les coordonnées polaires sont, avec les cartésiennes, celles que tu rencontreras le plus.
Elles sont principalement utilisées pour les mouvements de rotation.
Attention, les coordonnées polaires sont uniquement valables en 2 dimensions, en 3 dimensions on prendra les cylindriques que nous verrons juste après (et qui y ressemblent fortement).
Le principe est celui de la forme exponentielle du chapitre sur les complexes en mathématiques, à savoir le module et l’argument.
On se place dans le repère (O, ux, uy) puisque l’on est en 2D.
On prend un point M de ce plan : avec les coordonnées polaires, on le repère grâce à la distance OM, notée r, et à l’angle (ux, OM) noté θ :
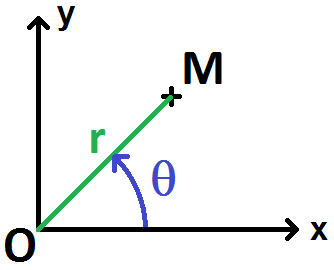
On voit bien ici le parallèle avec les complexes en maths : le r est appelé le module en maths, tandis que θ est l’argument.
Les notations r et θ utilisées en physique sont d’ailleurs les mêmes qu’en mathématiques.
On pose alors le vecteur ur dirigé selon OM mais normé, et uθ orthogonal à ur (faisant un angle π/2 avec ur) :
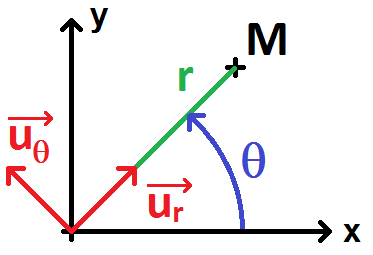
On remarque que si θ = 0, ur coïncide avec ux et uθ avec uy.
—
Autrement dit, le repère polaire est obtenu par rotation du repère cartésien d’un angle θ.
On peut également dire que le repère cartésien est obtenu par rotation du repère polaire d’un angle -θ (on se servira de cela dans les démonstrations).
—
On voit bien ici que le repère polaire tourne quand le point M se déplace, il n’est pas fixe comme le repère cartésien.
ur est ainsi défini par :
\(\displaystyle \overrightarrow{u_r} = \frac{\overrightarrow{OM}}{||\overrightarrow{OM}||} \)
Remarque : la distance OM que l’on a noté r est parfois notée ρ (rho) dans certains livres ou par certains professeurs.
Il est préférable d’utiliser r pour ne pas confondre avec l’angle φ utilisé pour les coordonnées sphériques.
A noter que parfois le repère est mis au niveau du point M, cela ne change absolument rien :
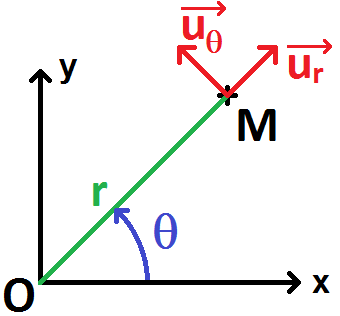
Attention, si les coordonnées du point M sont (ρ, θ) dans le repère polaire, on a :
\(\displaystyle \overrightarrow{OM} = r \overrightarrow{u_r} \)
—
L’angle θ n’apparaît pas dans l’expression du vecteur alors qu’il apparaît dans les coordonnées du point, contrairement aux coordonnées cartésiennes où toutes les coordonnées du point se retrouvaient dans l’expression du vecteur.
—
Enfin, les coordonnées de ur et uθ dans la base polaire sont :
\(\displaystyle \overrightarrow{u_r} (1 \, ; \, \theta) \)
\(\displaystyle \overrightarrow{u_{\theta}} (1 \, ; \, \theta + \frac{\pi}{2}) \)
—
ATTENTION !! Les coordonnées de ur en polaire ne sont pas (1;0) et celles de uθ ne sont pas (0;1), le principe n’est pas le même qu’en cartésiennes, car les coordonnées correspondent aux valeurs de r et θ.
—
Voyons maintenant les calculs permettant de passer d’un repère à un autre.
Le principe des coordonnées polaires étant le même que pour les complexes en maths, les formules seront les mêmes.
Nous allons les démontrer à partir du schéma suivant :
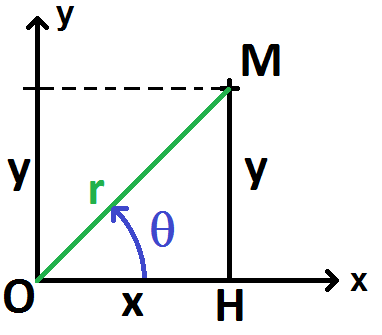
Dans le triangle OHM, d’après le théorème de Pythagore, on a :
\(\displaystyle r = \sqrt{x^2 + y^2} \)
De plus, tan(θ) = y/x, donc :
\(\displaystyle \theta = arctan(\frac{y}{x}) \)
Ces 2 formules permettent de passer des coordonnées cartésiennes aux coordonnées polaires.
Pour aller dans l’autre sens, on va toujours se placer dans le triangle OHM :
cos(θ) = x/r
sin(θ) = y/r
Donc :
\(\displaystyle x = rcos(\theta) \)
\(\displaystyle y = rsin(\theta) \)
Le passage d’un repère à l’autre est donc simple.
A partir de cela, on peut facilement exprimer les vecteurs de la base polaire en fonction des vecteurs de l’autre base.
En effet, dans la base polaire, ur a pour coordonnées (1,θ), donc en cartésiennes ses coordonnées sont (cos(θ), sin(θ)).
En effet : 1 × cos(θ) = cos(θ) et 1 × sin(θ) = sin(θ).
De même, dans la base polaire, uθ a pour coordonnées (1,θ + π/2), donc en cartésiennes ses coordonnées sont (-sin(θ), cos(θ)).
En effet : 1 × cos(θ + π/2) = -sin(θ) et 1 × sin(θ + π/2) = cos(θ).
On a donc :
\(\displaystyle \overrightarrow{u_r} = cos(\theta)\overrightarrow{u_x} + sin(\theta)\overrightarrow{u_y} \)
\(\displaystyle \overrightarrow{u_{\theta}} = -sin(\theta)\overrightarrow{u_x} + cos(\theta)\overrightarrow{u_y} \)
En inversant ces deux équations, on montre facilement que :
\(\displaystyle \overrightarrow{u_x} = cos(\theta)\overrightarrow{u_r} – sin(\theta)\overrightarrow{u_{\theta}} \)
\(\displaystyle \overrightarrow{u_y} = sin(\theta)\overrightarrow{u_r} + cos(\theta)\overrightarrow{u_{\theta}} \)
Remarque : on pourrait également dire que le repère cartésien est obtenu par rotation du repère polaire d’un angle -θ.
Ainsi ur a pour coordonnées (cos(θ); sin(θ)) en cartésiennes, donc ux a pour coordonnées (cos(-θ); sin(-θ)) en polaires, soit (cos(θ); -sin(θ)) : on retrouve la formule ci-dessus.
A partir de ces expressions, nous allons voir comment dériver ur et uθ par rapport au temps.
Mais pourquoi dériverait-on ces vecteurs par rapport au temps ?? 
Tout simplement parce qu’en mécanique, l’accélération est la dérivée de la vitesse, et la vitesse la dérivée du vecteur position :
\(\textstyle \overrightarrow{a} = \frac{d\overrightarrow{v}}{dt} \)
\(\textstyle \overrightarrow{v} = \frac{d\overrightarrow{OM}}{dt} \)
Si on est en cartésiennes, pas de problème car les axes sont fixes au cours du temps, donc :
\(\textstyle \frac{d\overrightarrow{u_x}}{dt} = \frac{d\overrightarrow{u_y}}{dt} = \frac{d\overrightarrow{u_z}}{dt} = 0 \)
Ainsi :
\(\textstyle \overrightarrow{v} = \frac{d\overrightarrow{OM}}{dt} \)
\(\textstyle \overrightarrow{v} = \frac{d(x\overrightarrow{u_x} + y\overrightarrow{u_y} + z\overrightarrow{u_z})}{dt} \)
Par linéarité :
\(\textstyle \overrightarrow{v} = \frac{dx}{dt}\overrightarrow{u_x} + \frac{dy}{dt}\overrightarrow{u_y} + \frac{dz}{dt}\overrightarrow{u_z} \)
Mais si on est en polaires :
\(\textstyle \overrightarrow{v} = \frac{d(r\overrightarrow{u_r})}{dt} \)
Comme r et ur varient au cours du temps, on a un produit u × v :
\(\textstyle \overrightarrow{v} = \frac{dr}{dt}\overrightarrow{u_r} + r\frac{d\overrightarrow{u_r}}{dt} \)
Et là tu vois quand doit dériver ur par rapport au temps !
Pour cela, on va exprimer ur en cartésiennes :
\(\textstyle \overrightarrow{u_r} = cos(\theta)\overrightarrow{u_x} + sin(\theta)\overrightarrow{u_y} \)
Dérivons par rapport au temps :
\(\textstyle \frac{d\overrightarrow{u_r}}{dt} = \frac{d(cos(\theta)\overrightarrow{u_x} + sin(\theta)\overrightarrow{u_y})}{dt} \)
\(\textstyle \frac{d\overrightarrow{u_r}}{dt} = \frac{d(cos(\theta))}{dt}\overrightarrow{u_x} + \frac{d(sin(\theta))}{dt}\overrightarrow{u_y} \)
N’oublions pas que θ dépend du temps (car le point M n’est pas fixe), on devrait donc écrire θ(t).
Pour dériver cos(θ), on peut écrire :
\(\textstyle \frac{d(cos(\theta))}{dt} = \frac{d(cos(\theta))}{d\theta} \times \frac{d \theta}{dt} \)
\(\textstyle \frac{d(cos(\theta))}{dt} = -sin(\theta) \times \frac{d \theta}{dt} \)
De la même manière :
\(\textstyle \frac{d(sin(\theta))}{dt} = \frac{d(sin(\theta))}{d\theta} \times \frac{d \theta}{dt} \)
\(\textstyle \frac{d(sin(\theta))}{dt} = cos(\theta) \times \frac{d \theta}{dt} \)
On a vu que :
\(\textstyle \frac{d\overrightarrow{u_r}}{dt} = \frac{d(cos(\theta))}{dt}\overrightarrow{u_x} + \frac{d(sin(\theta))}{dt}\overrightarrow{u_y} \)
D’où :
\(\textstyle \frac{d\overrightarrow{u_r}}{dt} = -sin(\theta)\frac{d\theta}{dt}\overrightarrow{u_x} + cos(\theta)\frac{d\theta}{dt}\overrightarrow{u_y} \)
\(\textstyle \frac{d\overrightarrow{u_r}}{dt} = \frac{d\theta}{dt}(-sin(\theta)\overrightarrow{u_x} + cos(\theta)\overrightarrow{u_y}) \)
On reconnaît l’expression de uθ !
Ainsi :
\(\textstyle \frac{d\overrightarrow{u_r}}{dt} = \frac{d\theta}{dt}\overrightarrow{u_{\theta}} \)
La dérivée par rapport au temps se note avec un point au-dessus, ce qui donne :
\(\displaystyle \dot{\overrightarrow{u_r}} = \dot{\theta}\overrightarrow{u_{\theta}} \)
De façon similaire, on pourrait montrer (entraîne-toi à le faire), que :
\(\displaystyle \dot{\overrightarrow{u_{\theta}}} = -\dot{\theta}\overrightarrow{u_r} \)
Remarque : dans le cas d’un mouvement circulaire, le theta point correspond à la vitesse angulaire, en rad.s-1. Si la vitesse de rotation est constante, theta point est constant. Le theta point est souvent noté ω.
Pour retenir facilement ces deux formules, il y a un moyen mnémotechnique très simple : dériver par rapport au temps revient à faire une rotation de π/2 et à multiplier par theta point.
En effet, si on prend ur et qu’on le fait tourner de π/2, on trouve uθ, et on multiplie par theta point, ce qui donne :
\(\textstyle \dot{\overrightarrow{u_r}} = \dot{\theta}\overrightarrow{u_{\theta}} \)
Et si on prend uθ et qu’on le fait tourner de π/2, on trouve –ur, et on multiplie par theta point, ce qui donne :
\(\textstyle \dot{\overrightarrow{u_{\theta}}} = -\dot{\theta}\overrightarrow{u_r} \)
—
Dériver ur ou uθ par rapport au temps revient à faire une rotation de π/2 et à multiplier par theta point.
—
Tout cela est résumé dans cette vidéo qui reprend les démonstrations ci-dessus.
Voyons alors les expressions de la vitesse et de l’accélération en coordonnées polaires :
\(\textstyle \overrightarrow{v} = \frac{d(r\overrightarrow{u_r})}{dt} \)
\(\textstyle \overrightarrow{v} = \dot{r}\overrightarrow{u_r} + r\dot{\overrightarrow{u_r}} \)
\(\displaystyle \overrightarrow{v} = \dot{r}\overrightarrow{u_r} + r\dot{\theta}\overrightarrow{u_{\theta}} \)
Pour l’accélération, on doit dériver cette expression, qui est une somme de deux produits, ça va donc être long !
Nous ne ferons donc pas la démonstration (mais tu peux la faire !) et donnerons uniquement le résultat :
\(\displaystyle \overrightarrow{a} = (\ddot{r} – r\dot{\theta}^2)\overrightarrow{u_r} + (r\ddot{\theta} + 2\dot{r}\dot{{\theta}})\overrightarrow{u_{\theta}} \)
La coordonnée selon ur est appelée accélération radiale.
La coordonnée selon uθ est appelée accélération orthoradiale.
Ces expressions se simplifient selon les exercices. Si par exemple le mouvement est circulaire, r est constant, donc les dérivées première et seconde de r sont nulles. Si en plus le mouvement est uniforme, on a theta point constant donc theta point point est nul.
On obtient ainsi :
\(\textstyle \overrightarrow{a} = -r\dot{\theta}^2\overrightarrow{u_r} \)
On retrouve que l’accélération est centripète dans le cas d’un mouvement circulaire uniforme comme on l’avait vu dans le chapitre sur les lois de Kepler.
Tu peux apprendre si tu veux les deux formules ci-dessus mais il est surtout important que tu saches les redémontrer !
Passons maintenant aux coordonnées cylindriques.
Les coordonnées cylindriques correspondent aux coordonnées polaires mais en rajoutant l’axe z, qui est le même qu’en coordonnées cartésiennes :
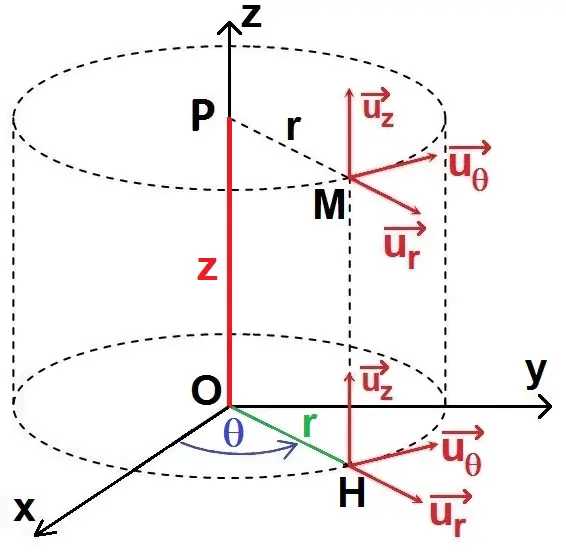
Le repère en coordonnées cylindriques est (O, ur, uθ, uz), l’axe uz étant confondu avec celui des coordonnées cartésiennes (ce pourquoi il s’appelle de la même manière), tandis que ur, uθ correspondent au repère polaire vu précédemment.
Le point M a pour coordonnées (r, θ, z).
Le point H est la projection du point M sur le plan (O, x, y), on peut écrire :
\(\textstyle \overrightarrow{OM} = \overrightarrow{OH} + \overrightarrow{HM} \)
OH est dans le plan (x ; y), et s’exprime comme en polaires, tandis que HM est selon l’axe (O, z) :
\(\textstyle \overrightarrow{OM} = r\overrightarrow{u_r} + z\overrightarrow{u_z} \)
Un point M dans le repère cylindriques est donc repéré par 3 coordonnées : (r, θ, z), mais le vecteur OM ne s’exprime qu’avec r et z : tout comme en polaire, le θ apparaît dans les coordonnées du point M mais pas du vecteur.
On peut dire que le repère polaire est un cas particulier du repère cylindrique : quand z est constant (on prend alors l’origine du repère au niveau de ce z).
Le repère polaire est utilisé quand le mouvement est en 2 dimensions, tandis que le cylindriques est utilisé en 3 dimensions.
Enfin, on peut noter que ce que l’on a vu précédemment sur le changement de repère en polaire et la dérivée des vecteurs ur et uθ reste vrai, mais il faut ajouter que l’axe (O, z) étant fixe, la dérivée temporelle de uz est nulle :
\(\textstyle \frac{d\overrightarrow{u_z}}{dt} = 0 \)
En 3 dimensions, on peut également utiliser les coordonnées sphériques, mais on va voir que les formules sont beaucoup plus complexes !
Les coordonnées sphériques font intervenir r, qui est la distance OM, et 2 angles θ et φ, selon le schéma suivant :
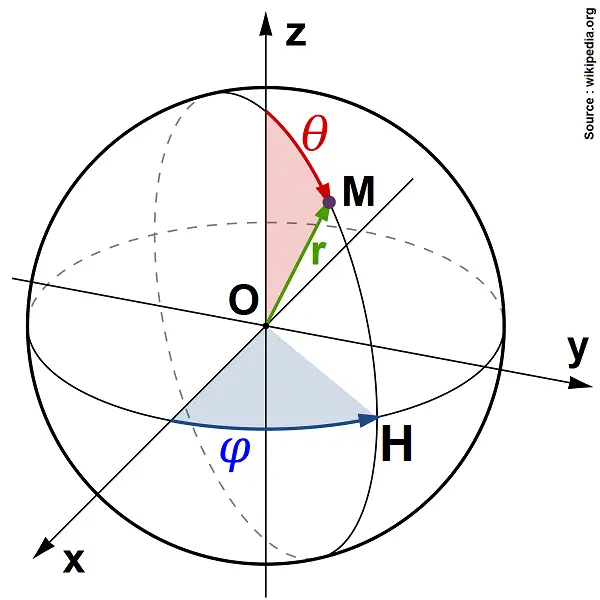
Le point H est la « projection » sur (O, x, y), mais ici il y a deux gros pièges !
Premier piège : l’angle φ correspond à l’angle θ des coordonnées cylindriques !!!
Deuxième piège : le r correspond à la longueur OM et non plus à la longueur OH comme en cylindriques.
—
Il faut donc faire très attention à ne pas confondre le θ en cylindriques qui n’est pas le même qu’en sphériques :
Le θ en cylindriques correspond au φ en sphériques.
De plus, r désigne ici la longueur OM, et non la longueur OH entre le centre et la projection comme en cylindriques.
—
—
MAIS ATTENTION !! Il peut arriver que le professeur utilise une autre convention et décide d’inverser le θ et le φ… 
Cela arrive parfois en maths par exemple, mais la convention décrite ci-dessus est la plus utilisée.
—
Le θ en sphériques correspond, comme tu le vois sur le schéma, à l’angle entre (O, z) et le vecteur OM :
\(\textstyle \theta = (\overrightarrow{u_z} ; \overrightarrow{OM}) \)
Le φ correspond quant à lui à l’angle entre (O, x) et le vecteur OH :
\(\textstyle \phi = (\overrightarrow{u_x} ; \overrightarrow{OH}) \)
Si tu connais un peu le principe de la latitude et de la longitude, cela devrait te rappeler quelque chose.
En effet, pour repérer un point de la Terre, on utilise les coordonnées GPS, qui correspondent à la latitude et la longitude :
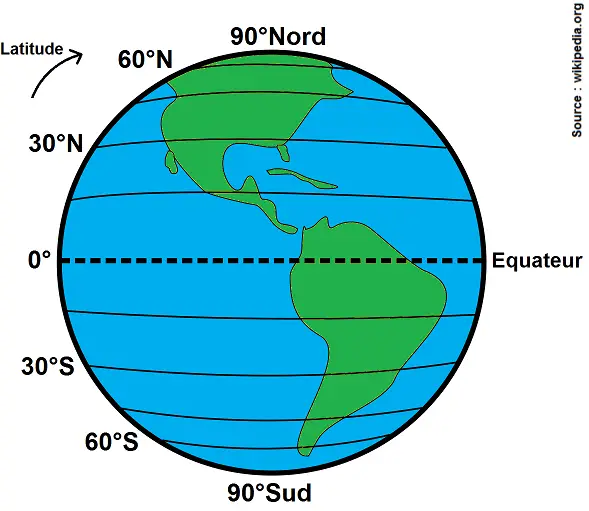
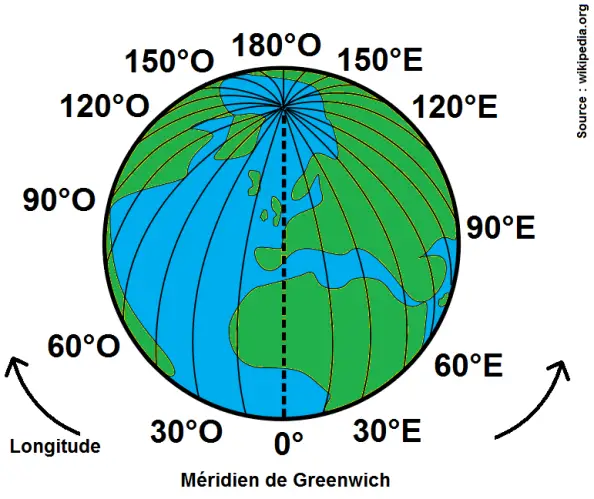
En donnant la latitude et la longitude, on obtient un point unique.
Mais tu as sans doute remarqué que la latitude se mesure par rapport à l’équateur, alors que θ se mesure par rapport au pôle nord !!
θ est donc le complémentaire de la latitude, ce pourquoi θ est appelée la colatitude.
φ correspond en revanche bien à la longitude.
Pour un point sur Terre, le r est évidemment égal au rayon de la Terre, ce pourquoi ce n’est pas précisé dans les coordonnées GPS.
Le point M est ainsi repéré par 3 coordonnées (r, θ, φ), mais le vecteur OM n’est repéré que par r :
\(\textstyle \overrightarrow{OM} = r\overrightarrow{u_r} \)
Le changement de repère avec les coordonnées cartésiennes a des expressions assez complexes, ce qui fait qu’il est moins fréquemment utilisé que les autres.
Tu peux t’entraîner à démontrer les formules ci-dessous, ce n’est pas trop compliqué (il s’agit de raisonner avec le point P et avec la projections du point M sur l’axe z) :
\(\displaystyle x = rsin(\theta)cos(\phi) \)
\(\displaystyle y = rsin(\theta)sin(\phi) \)
\(\displaystyle z = rcos(\theta) \)
A l’inverse, on peut exprimer r, θ et φ en fonction de x, y et z :
\(\displaystyle r = \sqrt{x^2 + y^2 + z^2} \)
\(\displaystyle \theta = arccos(\frac{z}{r}) \)
\(\displaystyle \phi= arctan(\frac{y}{x}) \)
Ces formules se démontrent facilement à partir des 3 formules précédentes.
On utilise les coordonnées sphériques quand on a un objet ou un mouvement à symétrie centrale (sphère, rotule etc…), tandis que l’on utilisera les coordonnées cylindriques quand on a un objet ou un mouvement à symétrie axiale (cylindre, ressort, etc…).
Les exercices sur ce chapitre seront bientôt disponibles !
Sommaire des coursHaut de la page



très éficace
superbes explications je comprends enfin les trois systèmes de coordonnées merci beaucoup à vous
incroyable, j’avais un blocage avec les bases en polaires.
la remarque :
« —
ATTENTION !! Les coordonnées de ur en polaire ne sont pas (1;0) et celles de uθ ne sont pas (0;1), le principe n’est pas le même qu’en cartésiennes, car les coordonnées correspondent aux valeurs de r et θ.
— » m’a tout fait comprendre !
merci beaucoup
Merci beaucoup