Les circuits RL et RC

Sommaire

Introduction
Les bobines
Etude d’un circuit RL
Aspect énergétique d’un circuit RL
Les condensateurs
Etude d’un circuit RC
Aspect énergétique d’un circuit RC
Exercices

Introduction

Dans ce chapitre, nous allons étudier les bobines, les condensateurs, ainsi que les circuits de base avec ces dipôles, à savoir les circuits RL et RC. Les circuits RLC, plus complexes, seront vus dans un chapitre séparé.
Il est fortement conseillé (voire obligatoire ) de bien maîtriser le chapitre sur les bases de l’électricité ainsi que le chapitre sur la loi d’ohm, car ils utilisent de nombreuses notions vues dans ces chapitres.
Par ailleurs, il est important de maîtriser les équations différentielles du 1er ordre. Si ce n’est pas le cas tu peux aller jeter un œil en cliquant ici pour voir le cours correspondant.

Les bobines

Haut de page

Commençons par étudier les bobines.
Une bobine est constituée d’un fil conducteur enroulé autour d’un isolant, formant ainsi ce qu’on appelle des spires (souvent des cercles).
Le mieux est de le voir en photo :

Le symbole d’une bobine ressemble évidemment à un tel enroulement :

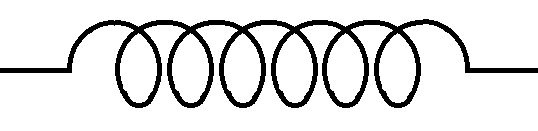
Une bobine est caractérisée par une inductance, notée L, en Henry (H).
Par exemple L = 3,0 H.
L’inductance L est une constante, elle ne dépend pas du temps.

La bobine a également une résistance interne, notée r, en ohms (r minuscule pour ne pas confondre avec les autres résistances).
Souvent la résistance interne r sera négligée par rapport aux autres résistances du circuit.
Quand le r est négligé, on parle de bobine idéale.

On a alors deux notations, l’une faisant apparaître la résistance interne, l’autre non :

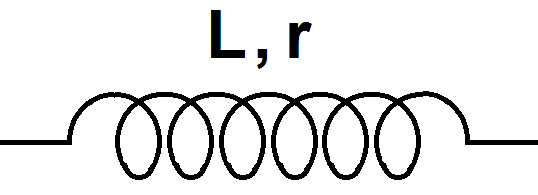
ou

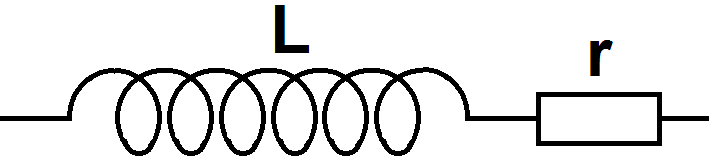
Quelle est le principe de fonctionnement d’une bobine ?
Sans rentrer dans les détails, le courant va passer dans le fil. Si le courant est variable, cela va créer un champs magnétique qui va s’opposer au courant : c’est le phénomène d’auto-induction.
Il va alors se créer une tension qui a pour expression :

ou, si on prend en compte r :

Dans un circuit, s’il y a plusieurs U et plusieurs i, on les note parfois U_L et i_L pour faire la différence.
A noter que ce sont des fonctions qui dépendent du temps, il faudrait donc noter U_L(t) et i_L(t) mais pour simplifier le t ne sera pas écrit la plupart du temps.

Ces formules sont évidemment valables en convention récepteur :

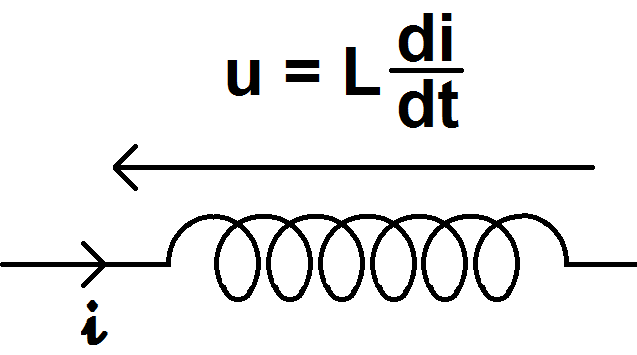
Ainsi, en négligeant r, et si i ne varie pas, di/dt = 0, donc U = 0 ! La bobine se comporte alors comme un fil (ou une résistance si on prend en compte r).
Donc une bobine n’a un rôle qu’en régime variable, pas en régime permanent.
On verra d’ailleurs que dans les circuits RL, une fois le régime transitoire passé, c’est comme s’il n’y avait pas de bobine.

—
En régime permanent, une bobine se comporte comme un fil (si on néglige la résistance interne).
—

Voyons maintenant l’énergie emmagasinée par une bobine, parfois notée E_L pour signifier qu’il s’agit de l’énergie de la bobine.
On a la relation :

Le i étant évidemment le courant qui traverse la bobine.

On se servira de cette relation dans l’étude de l’aspect énergétique des circuits électriques où il y a des bobines.

Cette énergie E_L étant continue au cours du temps, on en déduit que i est continue au cours du temps.

—
L’intensité traversant une bobine est continue au cours du temps.
—

On se servira assez souvent de cette propriété, notamment pour trouver les conditions initiales dans un circuit.

Enfin, terminons par les associations de bobines : les lois sont les mêmes que pour les résistances.
Ainsi, quand on met des bobines en série, leurs inductances s’additionnent pour donner une inductance équivalente L_éq.

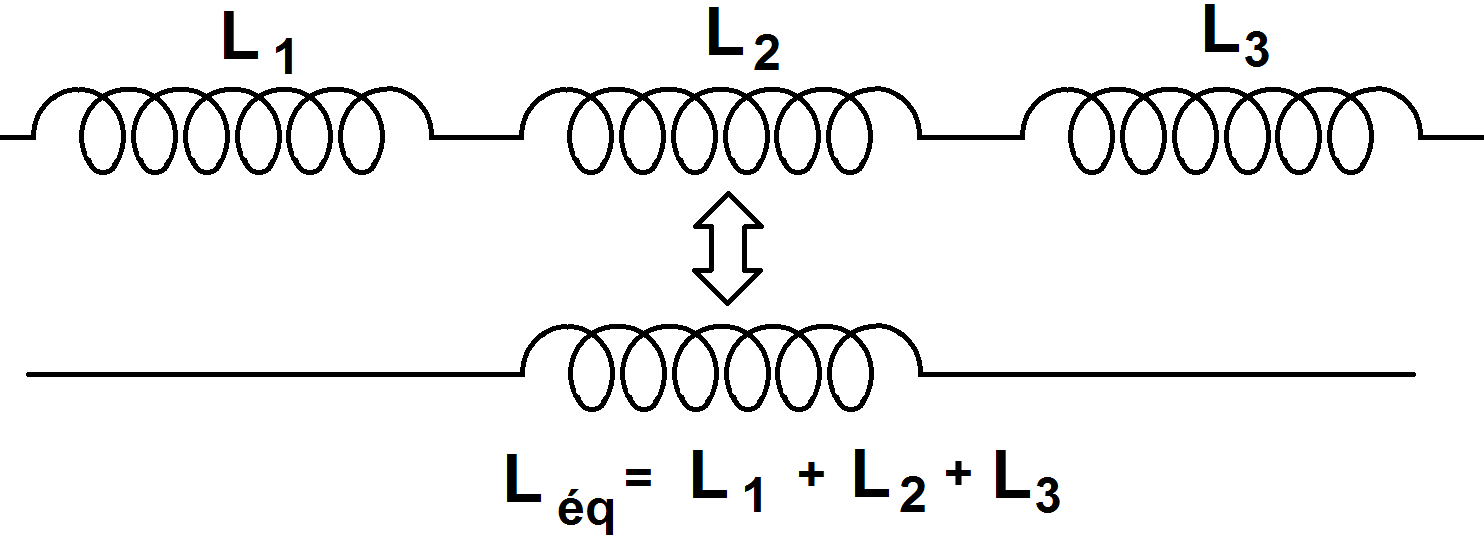
Quand on met des bobines en parallèle, l’inverse de leurs inductances s’additionnent pour donner l’inverse d’une inductance équivalente 1/L_éq.

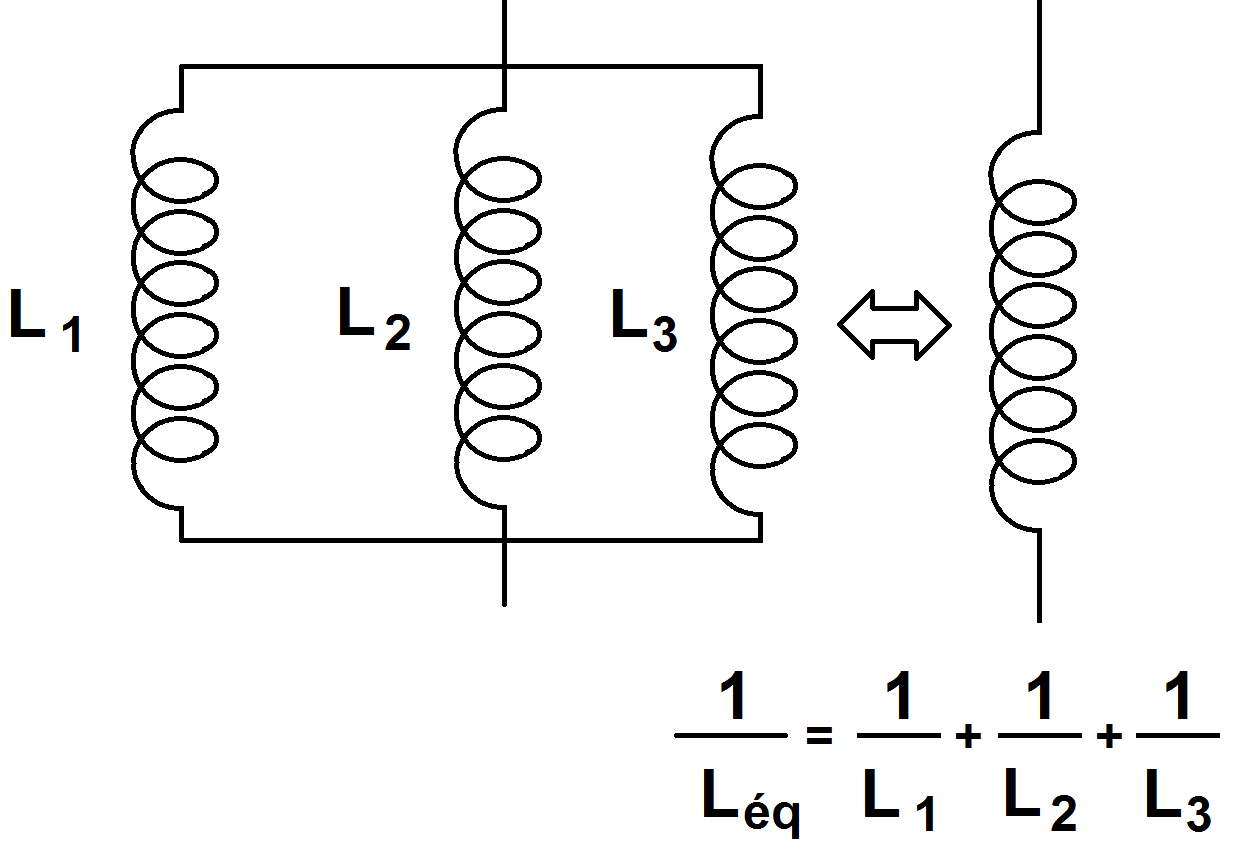
Les exemples sont pris avec 3 bobines mais le principe est le même avec plus de bobines !

Passons maintenant à l’étude d’une bobine dans un circuit, le cas le plus simple étant un circuit RL.

Etude d’un circuit RL

Haut de page

Ce que l’on appelle un circuit RL, c’est un circuit comprenant une résistance R et une bobine d’inductance L (on néglige r).
Comme il faut une source d’énergie, on rajoute un générateur de tension e(t) :

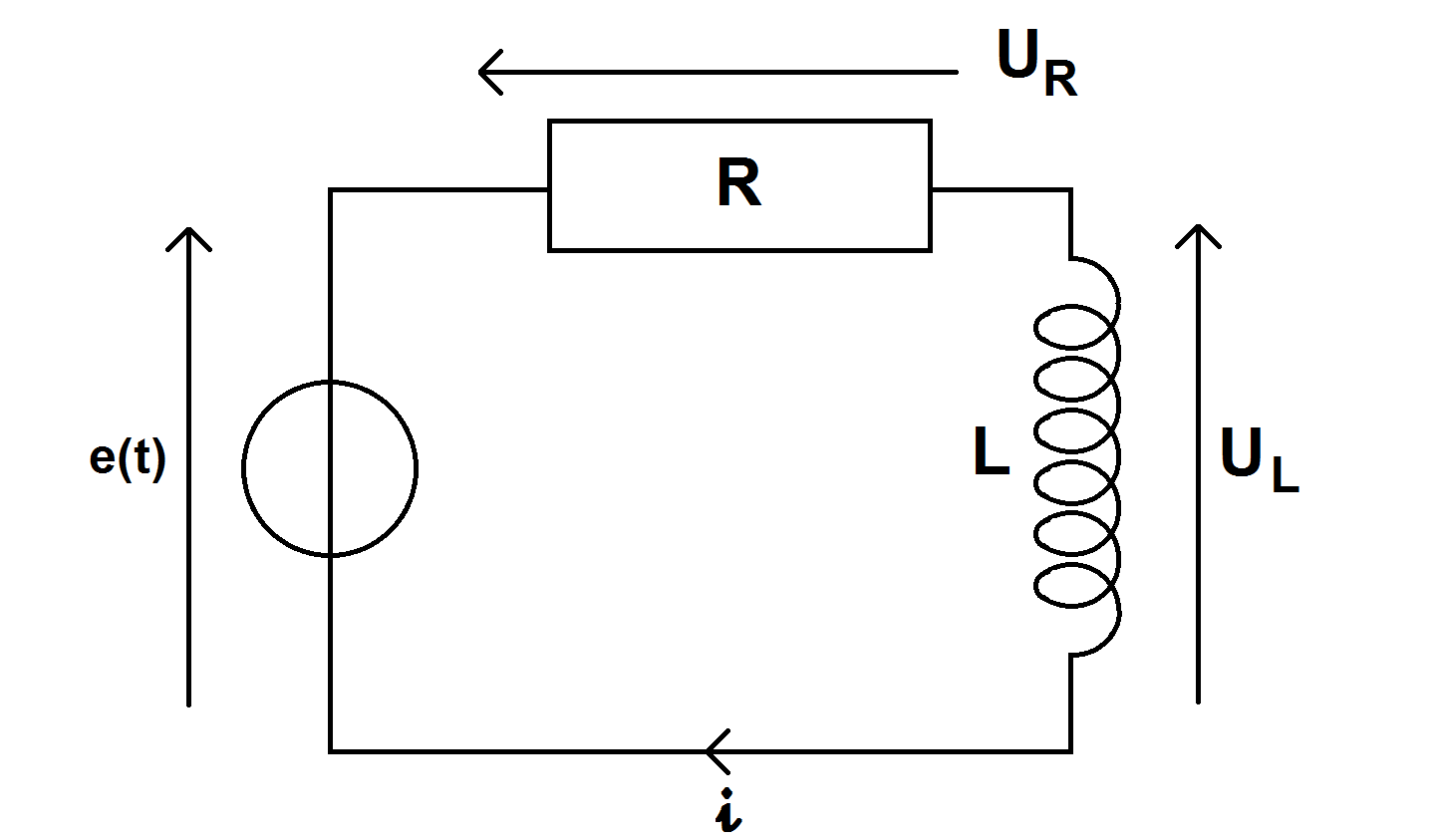
Comme il n’y a qu’une seule boucle, le i est le même dans tout le circuit.
Il y a en revanche 3 tensions : e, U_R et U_L.
L’objectif est de trouver l’expression au cours du temps de i, U_R et U_L.
Et e(t) alors ??
Le e(t) est imposé, ici nous prendrons un échelon de tension car c’est le cas le plus intéressant à étudier.
Cela signifie que la tension aux bornes du générateur est nulle avant t = 0, et vaut une constante E à partir de t = 0 :

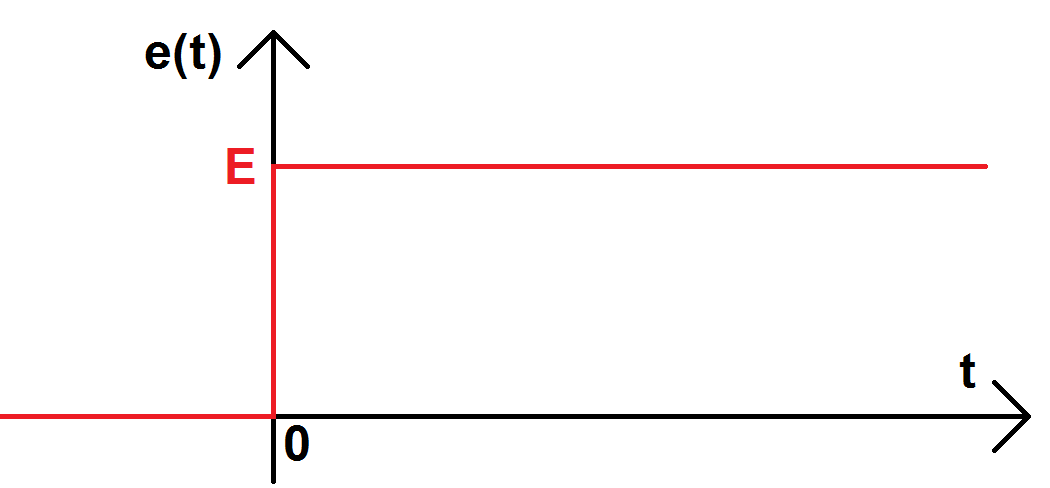
On a donc e(t) = 0 pour t < 0 et e(t) = E pour t ≥ 0.

Il faut donc chercher i, U_R et U_L.
Quand on a i, on a U_R d’après la loi d’ohm U_R = Ri.
Quand on a i, on a U_L puisque U_L = Ldi/dt.

On va donc chercher i !

On ne peut pas commencer par la loi des nœuds puisqu’il n’y a qu’une seule boucle, on commence donc par la loi des mailles :

On remplace :

On obtient une équation différentielle en i : on divise alors par L pour que le coefficient de la plus grande dérivée vaille 1 :

On trouve ainsi la forme canonique d’une équation différentielle d’ordre 1 que l’on a appris à résoudre.
On avait alors vu que l’on posait une constante de temps τ (tau) qui est l’inverse du coefficient de la fonction sans dérivée.
Ici le coefficient de i est R/L, donc la constante de temps est l’inverse, c’est-à-dire L/R :

Il s’agit de la constante de temps d’un circuit RL (à apprendre par cœur !).

L’équation devient alors :

Résolvons cette équation.
1ère étape : résoudre l’équation homogène (sans second membre)

La solution, notée i₁ est :

avec k constante réelle à déterminer.

Attention à ne pas déterminer la constante maintenant, seulement après la deuxième étape !

2ème étape : trouver une solution particulière
Si on cherche comme solution particulière une constante notée i₂, on a di/dt = 0 (la dérivée d’une fonction constante est nulle).
D’où :

Or τ = L/R :

La solution totale est la somme des deux fonctions trouvées :

Il est maintenant temps de trouver la constante k. Celle-ci se détermine à partir des conditions initiales, c’est-à-dire à t = 0.
A t = 0, on sait que le générateur passe de 0 à E.
Ainsi pour t < 0, c’est comme si le générateur n’était pas allumé, donc il n’y a pas de courant !
Donc i(t) = 0 pour t < 0.
Or on a vu précédemment que le courant traversant la bobine était continu, donc i est continu !!
On en déduit que i(0) = 0 par continuité.

Remplaçons donc t par 0 dans l’expression trouvée précédemment :

Donc :

Il n’y a plus qu’à remplacer k dans l’expression de i :

Et on voit que l’on peut factoriser par E/R :

On sait que i(0) = 0, et pour t très grand, l’exponentielle tendra vers 0, et donc i tendra vers E/R : on a une asymptote horizontale.
Le tracé de i est le suivant :

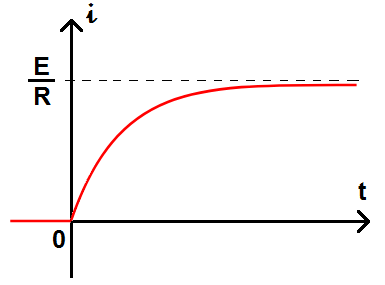
Comme tu le vois, la bobine ralentit la mise en place du courant dans le circuit. En effet, s’il n’y avait pas la bobine dans le circuit, l’intensité serait passée directement de 0 à E/R : il n’y aurait pas eu de régime transitoire.

Par ailleurs, on a vu dans le chapitre sur les équations différentielles d’ordre 1 que dans ce genre de solutions, 63% de la valeur finale est atteinte à t = τ.
De plus, la tangente à l’origine coupe l’asymptote à t = τ.
Graphiquement, cela donne :

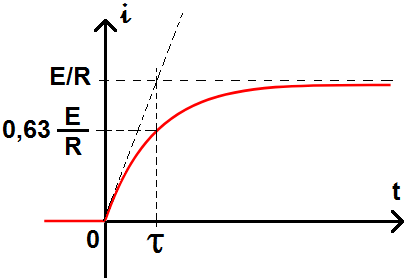
On peut considérer qu’à t = 5 τ le régime permanent est atteint.

Le τ mesure la rapidité du système à établir le régime permanent : comme τ = L/R, on peut faire varier la valeur de L et R pour rendre le système plus rapide ou au contraire plus lent.
Plus τ est petit, plus le régime permanent s’établira rapidement.

Maintenant que l’on a i, on peut calculer U_R et U_L !
U_R se calcule facilement avec la loi d’ohm U_R = Ri : U_R est proportionnel à i donc on a la même courbe mais l’asymptote sera E et non E/R : cela n’a pas trop d’intérêt.

Pour U_L en revanche, c’est autre chose.

Il faut donc dériver i par rapport au temps, ce qui donne :

On remplace τ :

Si on trace, on obtient :

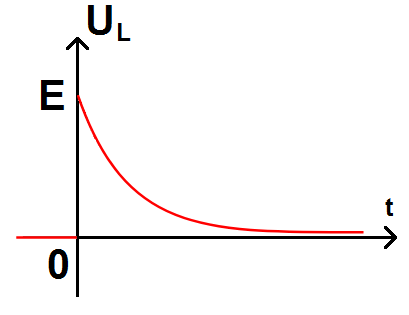
On constate que U_L est discontinue (la tension passe de 0 à E), contrairement à i qui était continue!

On peut rajouter, comme sur la courbe précédente, la tangente à l’origine qui coupe l’axe des abscisses à t = τ, valeur pour laquelle 37% de la valeur initiale est atteinte :

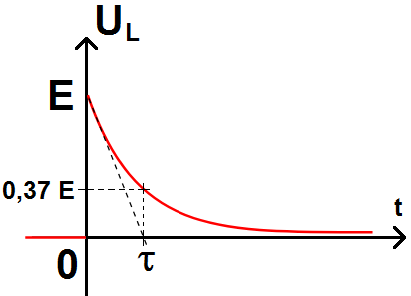
Par ailleurs, aurait-on pu prévoir les valeurs de U_L à t = 0 et en régime permanent ?
Oui !
En effet, d’après la loi des mailles : U_L + U_R = E
A t = 0, i = 0 donc U_R = 0, donc U_L = E.
En régime permanent, di/dt = 0 donc U_L = 0.

On retrouve par le calcul ce que l’on trouve graphiquement (heureusement ).

On a trouvé U_L à partir de i, que l’on a trouvé avec l’équation différentielle.
Une autre solution consiste à trouver l’équation différentielle en U_L et à la résoudre directement.

Reprenons la loi des mailles :

Puisque U_L = Ldi/dt, on ne peut pas transformer i en U_L : on doit donc dériver cette équation par rapport au temps :

R est constante, on peut la sortir de la dérivée, et E est constante : sa dérivée vaut 0, d’où :

Il n’y a plus qu’à remplacer di/dt :

Le coefficient de la plus grande dérivée est bien 1, on a donc la forme recherchée.
Comme précédemment, on pose τ = L/R (on retrouve évidemment la même constante de temps !) :

On retrouve une équation différentielle comme on les avait étudiées !
Ici il n’y pas de second membre donc on peut directement donner la solution :

Pour déterminer la constante, on utilise les conditions initiales.
Avec le même raisonnement que précédemment, on trouve i(0) = 0 (par continuité de i).
Donc d’après la loi d’ohm U_R(0) = 0, donc d’après la loi de mailles U_L(0) = E.

On remplace t par 0 dans U_L :
On a ainsi :

On retrouve l’expression vue plus haut en utilisant i !
Cette 2ème méthode est plus rapide pour calculer U_L mais il faut bien penser à dériver la loi des mailles pour arriver à l’équation différentielle en U_L.

Avant de passer à l’aspect énergétique de ce circuit, revenons sur un point que l’on a évoqué plus haut.
En régime permanent, on a U_L = 0, U_R = E et i = E/R.
S’il n’y avait pas de bobine dans le circuit (juste le générateur et la résistance), on aurait eu dès l’instant où on allume le générateur U_R = E et i = E/R.
Ainsi en régime permanent on arrive à la situation que l’on aurait eu dès le début s’il n’y avait pas de bobine : la bobine peut être remplacée par un fil, ce qui est confirmé par le fait que U_L = 0 en régime permanent.
Ainsi la bobine n’a d’effet qu’en régime transitoire : le courant s’établit progressivement au lieu de faire un saut de 0 à E/R.

Passons maintenant à l’aspect énergétique d’un circuit RL.

Aspect énergétique d’un circuit RL

Haut de page

Petit rappel : l’énergie E est reliée à la puissance P par la formule :

On met dE car il s’agit de l’énergie infinitésimale, pour avoir le E total il faut intégrer dE.
E est en Joules, la puissance en Watts et le t en secondes.
En électricité, la puissance est définie par :

D’où :

Attention à ne pas confondre l’énergie E avec la tension du générateur E !!
Pour ne pas mélanger, nous appellerons E_g l’énergie du générateur, de la même manière que l’on notera E_R l’énergie de la résistance et E_L celle de la bobine.

Pour une résistance :
dE_R = U_Ridt
dE_R = Ri²dt
Cette énergie correspond à l’énergie dissipée par effet Joule.

Pour le générateur :
dE_g = Eidt.
Il s’agit de l’énergie délivrée par le générateur pendant une période dt.

Pour une bobine (la tension U_L sera notée U) :

Repartons maintenant de la loi des mailles :

Multiplions par idt cette équation (c’est là l’astuce !) :

On retrouve les énergies de la bobine, de la résistance et du générateur : cette égalité traduit le fait que l’énergie fournie par le générateur est en partie dissipée par effet Joule dans la résistance, l’autre partie est stockée sous forme magnétique dans la bobine.

Passons maintenant aux condensateurs.

Les condensateurs

Haut de page

Un condensateur est constitué de 2 armatures conductrices (des plaques) séparées par un isolant appelé diélectrique.
Il est symbolisé de la manière suivante :

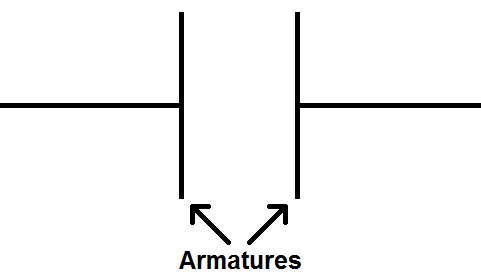
Quand un courant va traverser le condensateur, on a vu dans le chapitre sur les bases de l’électricité que les électrons arrivent en sens inverse.
Les électrons, négatifs, vont s’accumuler sur une armature, qui va donc avoir une charge négative. Pour compenser, l’autre plaque va se charger positivement.
La plaque positive est donc celle par laquelle arrive le courant : on note +q et -q les charges des deux plaques.
De plus la tension aux bornes du condensateur est notée U_C :

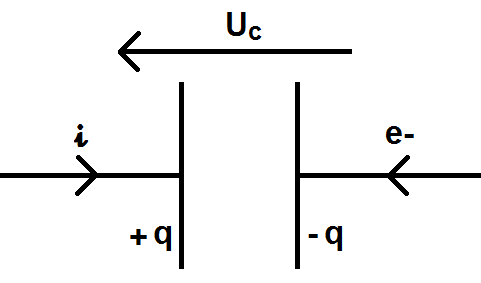
Un condensateur est caractérisée par une capacité notée C, en Farad (noté F).
Par exemple C = 5,2 F.

—
ATTENTION !! Ne pas confondre C, la capacité, avec l’unité de q qui est en Coulomb C…
On a par exemple C = 3,6 F et q = 12 C.
Oui ce n’est pas très pratique en effet…
—

La capacité C caractérise la possibilité pour le condensateur d’accumuler des charges sur ses armatures : plus C est grand, plus q pourra être grand. Mais q dépend aussi de la tension U_C appliquée aux bornes du condensateur.

En effet, on a la relation :

C’est très facile à retenir car phonétiquement CU se prononce comme la lettre q… un bon moyen mnémotechnique pour s’en souvenir !

Normalement la relation devrait s’écrire :

mais selon les exercices, la tension aux bornes du condensateur ne sera pas forcément notée U_C, mais évidemment dans la formule q = CU le U correspond à la tension aux bornes du condensateur.

—
Remarque importante : C est une constante, comme L pour les bobines.
En revanche, comme U peut varier, q peut varier : on devrait donc noter q(t) et U(t) mais pour simplifier on note souvent q et U.
—

Il y a une 2ème relation que l’on va utiliser avec les condensateurs :

Le i est évidemment le courant qui traverse le condensateur.

L’intérêt est de combiner les deux formules précédentes :

C étant une constante, on peut le sortir de la dérivée :

Et voilà, on vient de trouver la relation entre i et U !

—
Remarque : dans les exercices, tu ne peux pas utiliser cette formule directement, tu dois la redémontrer de la même manière que l’on vient de le faire (ça prend 3 lignes…).
En fait, tu peux la démontrer une fois pour toute ta copie, et après tu peux utiliser cette formule sans problème, mais il faut au moins la démontrer une fois !
—

A noter que cette formule ressemble très fortement à celle de la bobine, mais le rôle de i et U sont inversés : pour les bobines on dérive i, pour les condensateurs on dérive U, en revanche, le L comme le C sont dans les 2 cas les coefficients de la dérivée :

On a précisé U_L, i_L, U_C et i_C car dans un exercice il peut y avoir plusieurs i et U.
C’est aussi pour que tu fasses bien la différence et que tu comprennes que dans les 2 formules, les U et les i ne sont pas les mêmes.
Parfois le i peut être le même, si la bobine et le condensateur sont sur la même branche du circuit par exemple (ce sera le cas dans les circuits RLC).

—
Le fait que le rôle de i et U soient inversés pour les bobines et les condensateurs, mais que L et C aient la même place sera également vrai dans d’autres formules et principes.
—

Voyons maintenant l’aspect énergétique du condensateur : l’énergie emmagasinée par un condensateur, notée E_C est donnée par :

Cette formule ressemble là encore fortement à celle de la bobine :

Le principe énoncé juste avant est vérifié : L et C ont le même rôle, mais celui de i et U est inversé.
En effet, si dans la formule de l’énergie de la bobine on remplace L par C et i par U, on retrouve la formule pour le condensateur et réciproquement.

Comme pour les bobines, cette énergie est continue au cours du temps : on en déduit que U est continue au cours du temps !

—
La tension aux bornes d’un condensateur est continue au cours du temps.
—

A noter que pour les bobines c’est le courant qui est continu… le rôle de i est U est une fois de plus inversé !

Pour terminer, parlons des associations de condensateurs : le principe est l’inverse de celui des bobines, à savoir que quand on a des condensateurs en parallèle, leurs capacités s’additionnent, alors qu’en série c’est l’inverse de leurs capacités qui s’additionnent :

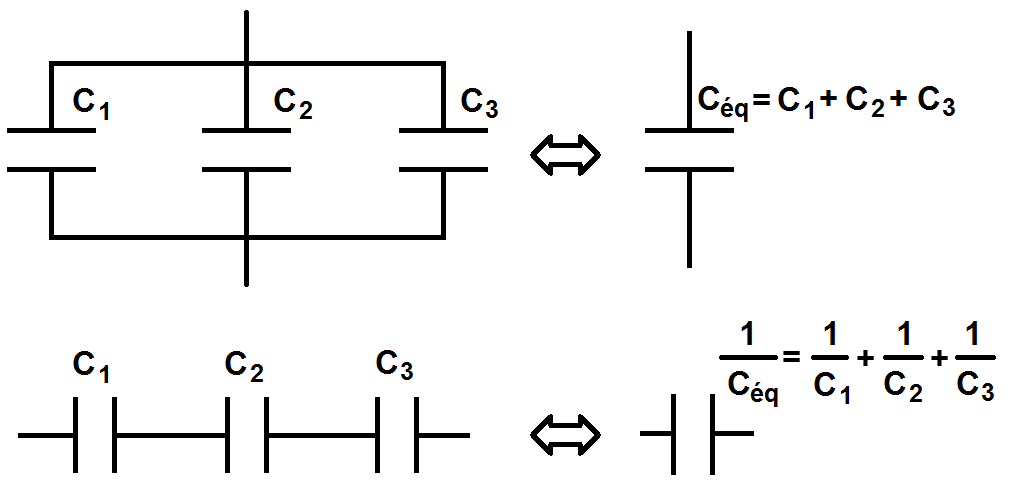
Les exemples ci-dessus, valables pour 3 condensateurs, sont évidemment valables pour n’importe quel nombre de condensateurs.

Passons maintenant à l’étude d’un condensateur dans un circuit, le cas le plus simple étant un circuit RC.

Etude d’un circuit RC

Haut de page

Ce que l’on appelle un circuit RC, c’est un circuit comprenant une résistance R et un condensateur de capacité C.
Comme il faut une source d’énergie, on rajoute un générateur E :

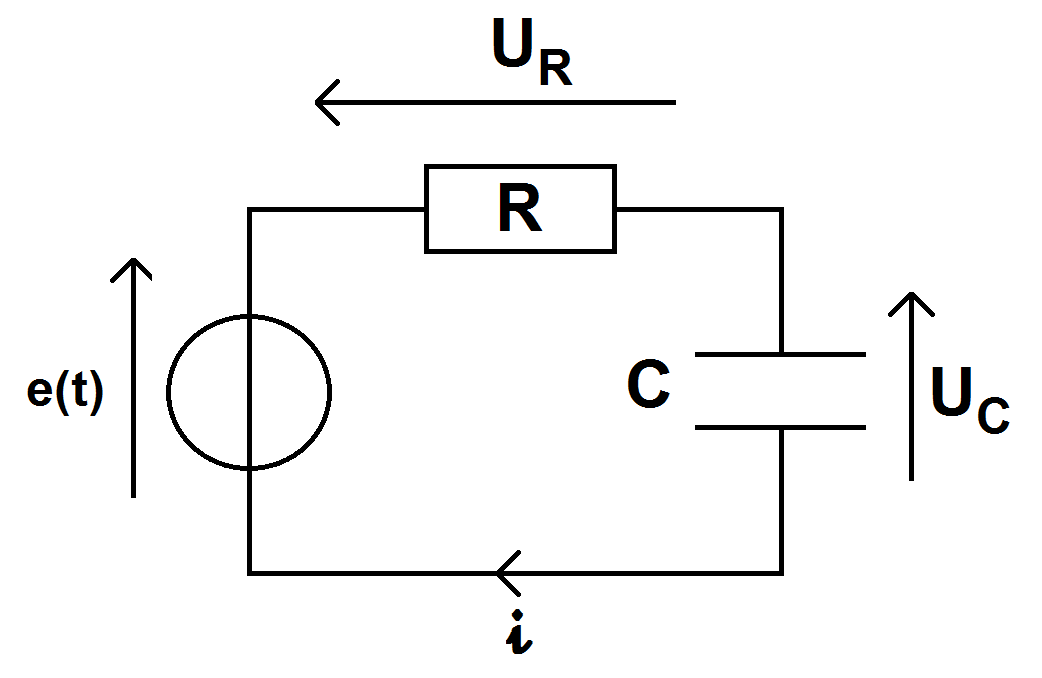
Comme tu vois, c’est exactement pareil qu’un circuit RL mais on remplace la bobine par un condensateur.
L’étude ainsi que les résultats de ce circuit devront donc être sensiblement les mêmes, mais avec le rôle du i et du U qui devraient être inversés d’après le principe énoncé précédemment.
Vérifions que c’est bien le cas !

Le but est ici de trouver i, U_R et U_C, la tension du générateur étant un échelon de tension comme pour le circuit RL.
A partir de U_C on aura i puisque i = CdU_C/dt.
On va donc chercher U_C !

Pour simplifier, U_C sera noté U par la suite.

Commençons par la loi des mailles :

Remplaçons i par l’expression démontrée plus haut :

Le coefficient de la plus grande dérivée devant être 1, on divise par RC :

Pour retrouver la forme souhaitée, on pose une constante de temps τ = RC :

On retrouve la même équation différentielle que pour i dans le circuit RL mais avec U à la place de i, et le second membre est légèrement différent.

Résolvons cette équation.
1ère étape : résoudre l’équation homogène (sans second membre)

La solution, notée U₁ est :

avec k constante réelle à déterminer.

Attention à ne pas déterminer la constante maintenant, seulement après la deuxième étape !

2ème étape : trouver une solution particulière
Si on cherche comme solution particulière une constante, on a dU/dt = 0 (la dérivée d’une fonction constante est nulle).
La solution particulière notée U₂ vérifie donc :

La solution totale est la somme des deux fonctions trouvées :

Il est maintenant temps de trouver la constante k. Celle-ci se détermine à partir des conditions initiales, c’est-à-dire à t = 0.
A t = 0, on sait que le générateur passe de 0 à E (échelon de tension).
Ainsi pour t < 0, c’est comme si le générateur n’était pas allumé, donc il n’y a pas de courant !
Donc i(t) = 0 pour t < 0, donc U_R = 0.
Et comme en plus e(t) = 0, on a d’après la loi des mailles U = 0 pour t < 0.
Or on a vu précédemment que la tension aux bornes du condensateur était continue, donc U est continue !!
On en déduit que U(0) = 0 par continuité.

On remplace t par 0 dans l’expression :

On remplace :

On factorise par E :

On retrouve quasiment la même expression que pour i dans le circuit RL (la constante est ici E, pour i c’était E/R).
La courbe va donc être évidemment la même (sauf l’asymptote) :

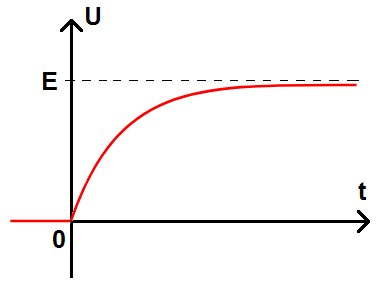
C’est ce que l’on appelle la charge du condensateur : il accumule des charges sur ses armatures, ce qui créé une tension à ses bornes : il peut par la suite se décharger dans un autre circuit et se transformer en générateur, c’est ce que l’on appelle la décharge du condensateur et que l’on verra en exercice.

Maintenant que l’on a U, on va pouvoir calculer i avec la formule que l’on avait démontrée :

Il faut donc dériver U par rapport au temps, ce qui donne :

On remplace τ :

Si on trace, on obtient :

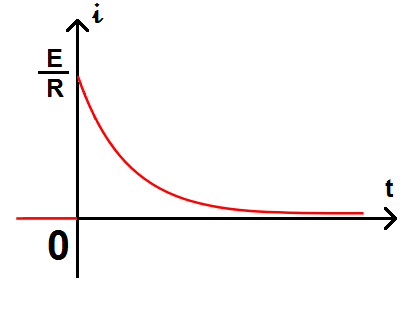
On constate que i est discontinue, contrairement à U qui était continue !
Pour la bobine c’était l’inverse : le rôle de i et U est donc bien inversé comme on l’avait dit, l’expression de i pour un circuit RC est quasiment la même que U pour un circuit RL et inversement, et dans un cas c’est i qui est continue, dans l’autre c’est U.

Aurait-on pu prévoir les valeurs de i à t = 0 et en régime permanent ?
Oui !
En effet, on a vu que par continuité U(0) = 0, donc d’après la loi des mailles E = U_R(0)
D’où E = Ri(0), et donc i(0) = E/R.
De plus, en régime permanent, dU/dt = 0 donc i = 0.

Tout est donc cohérent !

On a trouvé i à partir de U, mais aurait-on pu avoir i directement ?
Oui en effet, c’est exactement le même principe que pour le circuit RL, on aurait pu résoudre l’équation différentielle en i et non en U.
Voyons comment trouver cette expression.
On repart comme d’habitude de la loi des mailles :

Comme i = CdU/dt, on ne peut pas remplacer U : il faut donc, comme pour le circuit RL, dériver cette expression par rapport au temps :

R est constante, on le sort de la dérivée, et E est constant donc sa dérivée est nulle :

On divise par R pour le coefficient de di/dt soit 1 :

On pose τ = RC :

On retrouve la même équation différentielle que pour U dans le circuit RL (normal car on a dit que le rôle de i et U était inversé), une résolution similaire (que l’on ne fera pas car elle ressemble à ce que l’on a fait, mais tu peux t’entraîner à la faire ) aboutit à :

On retrouve l’expression trouvée précédemment mais plus rapidement puisque l’on n’est pas passé par U.

Terminons par l’aspect énergétique.

Aspect énergétique d’un circuit RC

Haut de page

L’énergie emmagasinée par le condensateur sera noté E_C.
U_C sera noté U pour simplifier.

On a vu que :
Pour une résistance :
dE_R = U_Ridt
dE_R = Ri²dt
Cette énergie correspond à l’énergie dissipée par effet Joule.

Pour le générateur :
dE_g = Eidt.
dE_g = EC(dU/dt)dt.
dE_g = ECdU

Pour un condensateur :

Repartons maintenant de la loi des mailles :

Multiplions par idt cette équation (la même astuce que pour RL !) :

On retrouve, comme pour le circuit RL, qu’une partie de l’énergie fournie par le générateur est dissipée par effet Joule, l’autre partie étant stockée sous forme électrique par le condensateur (et non sous forme magnétique comme le fait la bobine).

Mais en quelle proportion se fait cette dissipation et ce stockage d’énergie ?
Pour le savoir, nous allons intégrer les formules des énergies infinitésimales afin d’avoir l’énergie totale pendant toute la charge.
La variable étant dU, les bornes sont 0 et E puisque U varie de 0 à E pendant la charge.

Commençons par le générateur :

E et C sont des constantes :

L’intégrale vaut en effet E, elle est très simple à calculer.

Calculons l’énergie stockée dans le condensateur :

La primitive de U est U²/2 :

On retrouve la moitié de l’énergie fournie par le générateur : ainsi la moitié de l’énergie fournie par le générateur est dissipée par effet Joule dans la résistance, l’autre moitié est stockée sous forme électrique dans le condensateur.

Il est désormais temps de passer aux exercices !

Exercices

Haut de page

Tu trouveras sur cette page tous les exercices sur les circuits RL et RC !

Retour au sommaireHaut de la page